Случайная выборка 100 испытаний образцов бетона на прочность при сжатии приведена в табл. 1.

Таблица 1 – Выборка 100 испытаний образцов бетона

59,421	56,283	62,323	62,509	57,042	55,804	59,981	56,618	62,275	64,263
61,09	64,464	60,5	64,767	59,382	59,906	56,858	60,991	58,814	61,056
61,186	56,379	64,794	56,482	56,005	62,644	62,253	56,637	64,532	61,804
56,788	56,283	60,344	56,65	63,763	58,883	56,361	60,265	62,177	56,078
64,496	60,444	64,747	63,205	62,788	63,436	64,463	63,88	55,837	64,143
60,919	59,15	63,897	55,491	64,429	63,619	63,539	61,41	64,278	59,542
64,978	55,432	56,134	56,209	63,203	63	62,833	63,125	55,191	63,149
59,066	62,78	62,544	56,079	56,806	56,489	61,368	60,06	61,297	57,335
56,045	59,353	62,629	59,879	64,44	63,07	57,378	63,403	62,733	62,894
60,513	56,909	56,548	56,531	59,632	56,278	57,417	56,689	59,767	63,785

---

Необходимо приведенную выше выборку разделить на 10 разрядов и выделить из нее максимальные и минимальные значения.

Для определения интервала каждого из разрядов находим величину разряда как отношение разницы между граничными значениями выборки к общему количеству ее элементов:

.

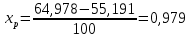Таблица 2 – Разграниченная выборка

		56,209
		56,278
		56,283
		56,283
		56,361
		56,379						62,177
		56,482						62,253	63,07	64,143
		56,489						62,275	63,125	64,263
		56,531			59,15			62,323	63,149	64,278
	55,191	56,548			59,353			62,509	63,203	64,429
	55,432	56,618			59,382			62,544	63,205	64,44
	55,491	56,637			59,421	60,265		62,629	63,403	64,463
	55,804	56,65			59,542	60,344		62,644	63,436	64,464
	55,837	56,689			59,632	60,444	61,09	62,733	63,539	64,496
	56,005	56,788			59,767	60,5	61,186	62,78	63,619	64,532
	56,045	56,806			59,879	60,513	61,297	62,788	63,763	64,747
	56,078	56,858	57,335	58,814	59,906	60,919	61,368	62,833	63,785	64,767
	56,079	56,909	57,378	58,883	59,981	60,991	61,41	62,894	63,88	64,794
	56,134	57,042	57,417	59,066	60,06	61,056	61,804	63	63,897	64,978
m	10	19	3	3	11	8	6	14	13	13

---

Произведем выборку данных для гистограмм, для этого в первой строке в порядке возрастания вдоль оси абсцисс записываются разряды, во второй – соответствующие им интервалы 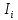, полученные следующим образом: 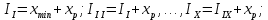в третьей строке указывается количество попаданий 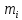значений случайной величины в соответствующий интервал; в четвертой строке записываются частоты соответствующих разрядов, которые вычисляют по формуле: .

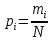Таблица 3 – Данные для гистограмм

	I	II	III	IV	V	VI	VII	VIII	IX	X
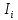	55,19	56,17	57,15	58,13	59,11	60,09	61,06	62,04	63,02	63,99
	56,17	57,15	58,13	59,11	60,09	61,06	62,04	63,02	63,99	64,98
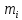	10	19	3	3	11	8	6	14	13	13
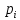	0,1	0,19	0,03	0,03	0,11	0,08	0,06	0,14	0,13	0,13

---

Построение гистограммы плотности распределения (рис. 1) выполняется следующим образом: вдоль оси абсцисс в порядке возрастания откладываются разряды, затем на каждом из разрядов как на основании строится прямоугольник, площадь которого равна частоте данного разряда. Таким образом, вдоль оси ординат откладываются значения .



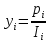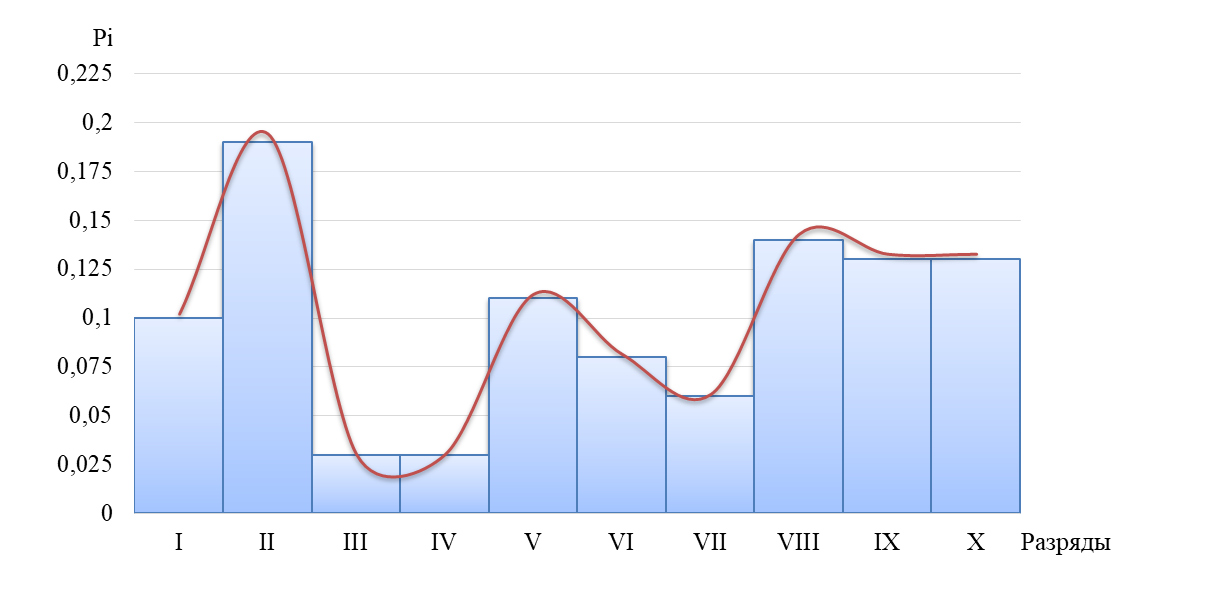
Рисунок 1 – Гистограмма плотности распределения

Гистограмма функции распределения (рис. 2) строится следующим образом: вдоль оси абсцисс в порядке возрастания откладываются разряды, а затем н каждом из разрядов строится прямоугольник, ордината которого равна сумме вероятностей (частот). Следовательно 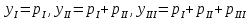и т.д.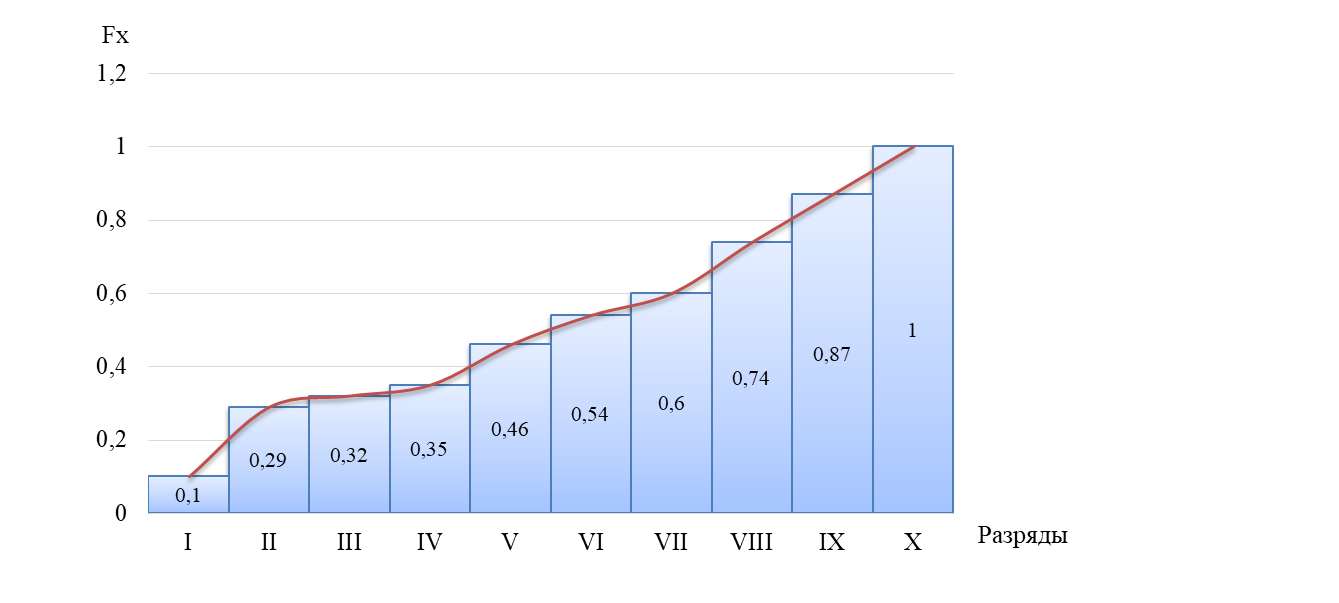



Рисунок 2 – Гистограмма функции распределения

Математическое ожидание (марочная прочность бетона) определяется по формуле:

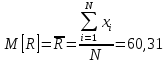МПа.

Дисперсия определяется по формуле:

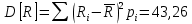МПа².

Среднеквадратическое отклонение определяется по формуле:

,

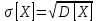Тогд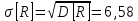а МПа.

Коэффициент вариации прочности бетона определяется по формуле:

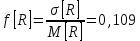, соответственно 10,9%.

На основании полученной информации определим класс бетона по формуле:

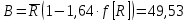МПа.

По ГОСТ 26633-2015 «Бетоны тяжелые и мелкозернистые» подберем класс бетона, ближайшее значение по прочности на сжатие составляет 52,39 МПа, что соответствует классу бетона В40.

---

Смотрите также файлы

• Эффект доплера и его использование в фармакобиологических исследованиях.docx

• Донорство как спасти каждого, которую выполнила обучающаяся 10 класса Петрова Софья Александровна.docx

• Линза.docx

• 2023 г. Планконспект проведения занятий по подготовке личного состава дежурных караулов 8 псч фпс гпс тема Культура и общие принципы пожарной разведки. Виды пожарной разведки. Вид занятия классногрупповой.docx

• Классическая теория эволюционизма и общественного прогресса Г. Спенсера.docx