ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Решение.
1. Для того чтобы вычислить среднее значение признака перейдем от интервального ряда к дискретному, то есть найдем середину каждого интервала как полусумму нижней и верхней границ. При этом величина открытого интервала первой группы приравнивается к величине интервала второй группы, а величина открытого интервала последней группы – к величине интервала предпоследней группы. Для удобства вычислений составляем таблицу.
| Стаж, число лет | Середины интервалов Xi' | fi | X'ifi | X'2ifi |
| до 5 | 2,5 | 12 | 30 | 75 |
| 5-10 | 7,5 | 18 | 135 | 1012,5 |
| 10-15 | 12,5 | 24 | 300 | 3750 |
| 15-20 | 17,5 | 32 | 560 | 9800 |
| 20-25 | 22,5 | 6 | 135 | 3037,5 |
| 25 и выше | 27,5 | 8 | 220 | 6050 |
| ИТОГО: | | 100 | 1380 | 23725 |
Найдем средний стаж:
= 
1380/100=13,8 лет2. Найдем моду Мо и медиану Ме:
Мо=ХМо + iМо
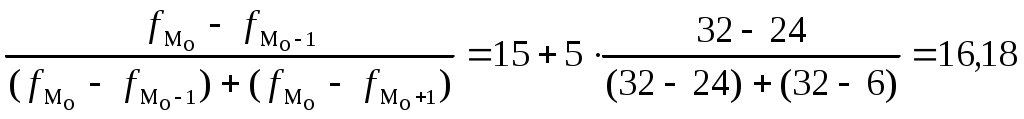летfM0,fM0-1,fM
+1 –частоты модального ,до и после модального интервалов соответственно,ХМ0 – начало модального интервала. iМО- величина модального интервала.
Мода показывает варианту наиболее часто встречающегося в данной совокупности, т.е. наиболее часто встречающийся стаж рабочих в данной совокупности равен 16,18%
Ме=ХМе + iМе
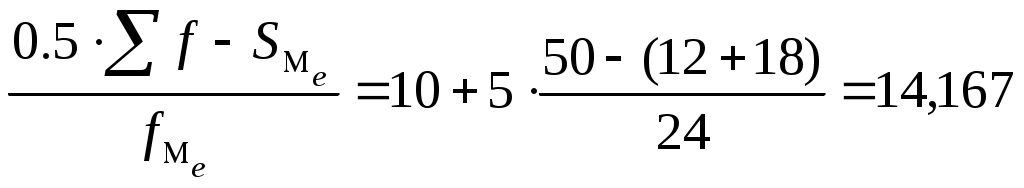летХМе- начало медианного интервала; iМе - величина медианного интервала;SМе- сумма накопленных частот до медианного интервала: fМе – частота медианного интервала.
Медиана – это варианта, располагающаяся в середине ранжированного ряда распределения.
Вывод: половина рабочих имеет стаж до 14,167 лет, а вторая половина рабочих – более 14,167 лет.
3. Найдем дисперсию по следующей формуле:
237,25-13,82 =46,81Дисперсия показывает среднее арифметическое квадратов отклонений каждого значения признака от средней арифметической.
Среднее квадратическое отклонение находим по специальной формуле:
= 6,84 летКоэффициент вариации
=(6,84/13,8)·100%=50%Когда относительные показатели вариации не превышают 35%, то принято считать, что полученные средние характеристики достаточно надежно характеризуют совокупность по варьирующему признаку. В нашем же случае, напротив, коэффициент вариации больше 35% -- не надежно, т.е. полученный средний стаж не надежно характеризует данную совокупность по этому признаку.
4. Из условия задачи имеем n/N=0