МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Тольяттинский государственный университет


РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ БАЛКИ

(УРАВНЕНИЕ ТРЕХ МОМЕНТОВ)

Методические указания для выполнения

расчетно-графической работы по курсу

“Строительная механика”

Тольятти 2004


УДК 624.041.2

ББК 38.112

Р 24

Р 24 Расчет статически неопределимой балки (уравнения трех моментов): Метод. указания. /Сост. Э.Р. Ефименко. Тольятти: ТГУ, 2005. 11 с.

Даны краткий теоретический материал для расчета статически неопределимой балки с помощью уравнения трех моментов и пример расчета дважды статически неопределимой балки.

Методические указания предназначены для студентов специальности 290300 “Промышленное и гражданское строительство”.


Научный редактор: старш.преподаватель Л.В. Ахмедьянова

Утверждено научно-методическим советом университета.

УДК 624.041.2

ББК 38.112


© Тольяттинский государственный университет, 2004.

Статически неопределимые неразрезные балки.
Неразрезной балкой называется брус, перекрывающий ряд пролетов и неразрывно связанный с опорами. Расчет неразрезных балок на шарнирно неподвижных опорах на действие вертикальной нагрузки ничем не отличается от расчета такой же балки на одной неподвижной и остальных подвижных опорах. Неразрезная балка при отсутствии промежуточных шарнирных включений столько раз статически неопределима, сколько промежуточных опор (при условии шарнирного опирания концов). Степень статической неопределимости определяется по формуле n_ст = С_оп - 3

Расчет неразрезной балки можно выполнить по общим правилам расчета статически неопределимых систем, применив метод сил. Расчет неразрезных балок производится с помощью уравнений 3-х моментов. Уравнения 3-х моментов – это преобразованные канонические уравнения метода сил для неразрезной балки. Преобразование уравнений происходит за счет выбора основной системы метода сил. В качестве основной системы берется система разрезных балок, полученная из заданной системы включением шарниров в опорные сечения. За неизвестные принимаются опорные изгибающие моменты. Число неизвестных усилий при этом равно числу промежуточных опор (при условии шарнирного опирания по концам балки). Таким образом, для расчета неразрезной балки необходимо составить столько уравнений трех моментов, сколько промежуточных опор (за исключением балок с жестким защемлением).

---

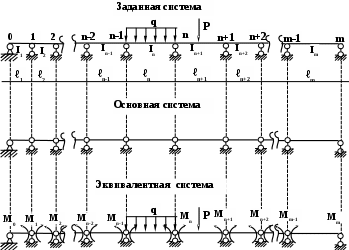
Преимущество выбранной основной системы заключается в том, что эпюры моментов от единичных усилий распространяются в ней только на два соседних пролета, и, стало быть, большее число побочных перемещений (единичных побочных коэффициентов) обращается в нуль. Таким образом, типовое n-ое каноническое уравнение метода сил, с учетом найденных единичных коэффициентов и грузовых членов примет следующий вид:
М_n-1· ℓ_n^'+ 2 М_n-1 · ( ℓ_n^' + ℓ_n+1^' ) + М_n+1 · ℓ_n+1^' = -6 · В _n ^ф · ℓ_n^' /ℓ_n - 6 А _n+1 ^ф · ℓ_n+1^' /ℓ_n+1 (1)
или в таком виде:
М_n-1· ℓ_n^'+ 2 М_n-1 · ( ℓ_n^' + ℓ_n+1^' ) + М_n+1 · ℓ_n+1^' = -6 · В _n ^ф · Ι_с /Ι_n - 6 А _n+1 ^ф · Ι_с /Ι _n+1 (2)
где ℓ_n^' , ℓ_n+1^' – приведенные длины пролетов, определяются по формулам:

ℓ_n^' = ℓ_n Ι_с /Ι_n ℓ_n+1^' = ℓ_n+1 Ι_с /Ι_n+1

Ι_с – произвольный момент инерции;

В _n ^ф – правая опорная реакция пролета ℓ_n от фиктивной нагрузки;

А _n+1 ^ф – левая опорная реакция пролета ℓ_n+1 от фиктивной нагрузки.

Величины фиктивных реакций определяются то таблице в зависимости от внешней нагрузки. Например:



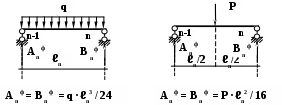
Полученные уравнение (1,2)– это уравнения трех моментов в общем виде.

Уравнение трех моментов выражает отсутствие в упругой линии угла перелома на

n

---

-ой опоре, т.е. представляет собой условие неразрезности балки на n-ой промежуточной опоре.

Если неразрезная балка имеет постоянное сечение, т.е.

I₁ = I₂ = . . . = I_n= I_n+1 = . . . = I_с , и ℓ₁^' = ℓ_{1 ,} ℓ₂^' = ℓ₂ , . . . , ℓ_n^' = ℓ_n , ℓ_n+1^' = ℓ_n+1 и т.д.

то уравнение трех моментов примет следующий вид:

М_n-1· ℓ_n+ 2 М_n-1 · ( ℓ_n + ℓ_n+1) + М_n+1 · ℓ_n+1 = -6 · В _n ^ф - 6 А _n+1 ^ф


Если конец неразрезной балки защемлен, то для применения уравнения трех моментов вводится дополнительный фиктивный пролет: ℓ₀ → 0, ЕI₀ = ∞. Т.е. в основной системе жесткие заделки на крайних опорах условно заменяются дополнительным пролетом бесконечно малой длины и бесконечно большой жесткости.




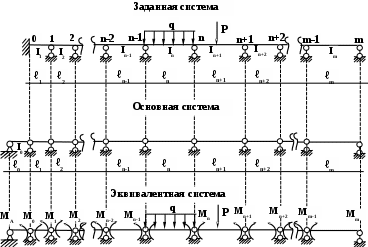
Е 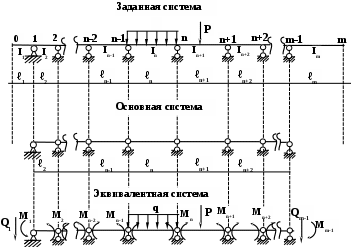сли у неразрезной балки есть консольные участки, то при построении основной системы метода сил эти участки отбрасываются и на эквивалентной системе действие этих участков на балку показывается в виде уже известных моментов и поперечных сил.

Определение усилий в сечениях неразрезной балки

и построение эпюр усилий.

Решая совместно канонические уравнения ( уравнения 3-х моментов), находим все неизвестные опорные моменты (М₁ , М₂ , … М_n ).

При расчете неразрезной балки на неподвижную нагрузку конечной целью является построение эпюр изгибающих моментов и поперечных сил .

Для получения эпюр моментов, первоначально над опорами неразрезной балки откладываем в виде отрезков, опорные моменты и концы отложенных ординат соединяем прямыми линиями (т.е. строим эпюру изгибающих моментов М_оп от опорных моментов). Затем в однопролетных шарнирно опертых балках (см. основную систему) строятся эпюры моментов от заданной внешней нагрузки М_Р⁰ . Сложив последние эпюры с соответствующими участками эпюры опорных моментов, получим окончательную эпюру изгибающих моментов

---

М_ок в неразрезной балке.

М_ок = М_оп + М_Р⁰

Аналогично строится эпюра поперечных сил: Q_ок = Q_оп + Q_Р⁰

Возможен и другой способ построения эпюры поперечных сил Q_ок . Этот способ был рассмотрен при расчете статически неопределимых рам методом сил.

Изгибающий момент и поперечную силу в произвольном сечении неразрезной балки определяют по формулам:

М_(х) = М_р⁰_(х) + М_n · x / ℓ_n + М_n-1 · ( ℓ_n – x ) / ℓ_n
Q_(х) = Q _р⁰_(х) + М_n / ℓ_n - М_n-1 / ℓ_n
М_р⁰_(х) , Q_р⁰_(х) - соответственно изгибающий момент и поперечная сила в рассматриваемом сечении х однопролетной шарнирно опертой балки с пролетом от заданной внешней нагрузки.

Опорная реакция R_n может быть определена как разность поперечных сил слева и справа от опоры n .

R_n = Q_n^(прав) - Q_n^(лев)

где Q_n^(прав) - поперечная сила, возникающая на n-ой опоры в пролете ℓ_n+1

Q_n^(лев) - поперечная сила, возникающая на n-ой опоры в пролете ℓ_n




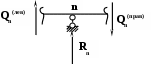
Порядок расчета неразрезной балки.

1. 
   Определить степень статической неопределимости.
   
2. 
   Выбрать основную и эквивалентную системы.
   
3. 
   Составить уравнения трех моментов.
   
4. 
   Решить систему уравнений. Найти неизвестные опорные моменты.
   
5. 
   Построить окончательную эпюру изгибающих моментов.
   
6. 
   Построить окончательную эпюру поперечных сил.
   
7. 
   Определить опорные реакции балки.
   
8. 
   Провести статическую проверку рамы в целом.
   

Вопросы для самоконтроля

1. 
   Дать определение неразрезной балки.
   
2. 
   Определение степени статической неопределимости балки.
   
3. 
   Выбор основной системы и построение эквивалентной системы.
   
4. 
   Записать уравнения 3-х моментов в общем виде, а также для балок постоянного сечения. Физический смысл этих уравнений.
   
5. 
   Дать понятие фиктивной опорной реакции. Примеры определения фиктивных опорных реакций от различных типов нагружения.
   
6. 
   Определение изгибающих моментов и поперечных сил в произвольном сечении неразрезной балки.
   
7. 
   Порядок построения окончательной эпюры изгибающих моментов.
   
8. 
   Порядок построения окончательной эпюры поперечных сил.
   
9. 
   Порядок определения опорных реакций в неразрезной балке.
   
10. 
    Расчет неразрезной балки с защемленным концом при помощи уравнения 3-х моментов (отличия расчета).
    
11. 
    Расчет неразрезной балки с консольными участками при помощи уравнения 3-х моментов (отличия расчета).
    

---

Порядок расчета неразрезной балки.


Пример расчета неразрезной балки.


q₁ = 2 (т / м) q₂ = 3 (т / м) Р = 5 (т)

ℓ₁= 6 ( м) ℓ₂ = 8 ( м) ℓ₃ = 4 ( м)

I₁= 2I I₂= I I₃= 2I







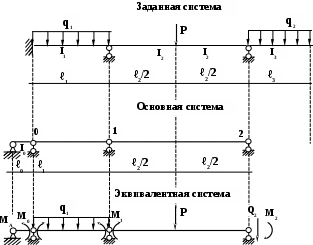
1. Определяем степень статической неопределимости балки:

n_ст = С_оп – 3 = 5 – 3 = 2

Таким образом, балка дважды статически неопределима. Необходимо отбросить две лишние связи и составить два уравнения (уравнения 3-х моментов).

2. Выбираем основную систему и строим эквивалентную . На основной системе отбрасываем внешнюю нагрузку, врезаем шарниры в опорные сечения, отбрасываем консольный участок и заменяем жесткую заделку дополнительным пролетом ℓ₀ бесконечно малой длины и бесконечно большой жесткости. На эквивалентной системе показываем внешнюю нагрузку, реакции отброшенных связей ( опорные моменты М₀ и М₁) и действие консольного участка в виде известного момента М₂ и поперечной силы Q_2.

3. Составляем уравнения трех моментов.

Исходя из выбранной основной системы видно, что неизвестными усилиями являются моменты М₀ и М₁. Момент М_А равен нулю, так как это момент в крайней шарнирной опоре (момент в шарнире). Момент М₂ определяется как момент от консольного участка на балку (аналогично определяется и Q₂ ) , т.е.

М₂ = - q₂ · ℓ₃ · ℓ₃ /2 = - 3 · 2 · 1 = - 6 (тм)

Q₂ = - q₂ · ℓ₃ = - 3 · 2 = - 6 (тм)

Так как неизвестными моментами М₀ , М₁ являются моменты на 0-ой и 1-ой опорах соответственно, то уравнения трех моментов составляются для n=0 и n=1 .

n=0 М_А· ℓ₀^' + 2 М₀ ·(ℓ₀^' + ℓ₁^' ) + М₁· ℓ₁^' = - 6 В₀^ф · I_с / I₀ - 6 А₁^ф · I_с / I₁

n=1 М₀· ℓ₁^' + 2 М₁ ·(ℓ₁^' + ℓ₂^' ) + М₂· ℓ₂^' = - 6 В₁^ф · I_с / I₁ - 6 А₂^ф · I_с / I₂

Предварительно найдем все необходимые величины для этих уравнений:

ℓ₀^' = ℓ₀ ·I

---

Смотрите также файлы

• Сфералы айналар, сфералы айна кмегімен кескін алу Оу масаты.docx

• Контрольная работа 1 по дисциплине Антикоррупционная политика и законодательство рф.docx

• Программа Вокального кружка Веселые девчата.docx

• Доклад соб о готовности к ведению огня.doc

• Исследование характеристик операционного усилителя.docx