Файл: санктпетербургский университет аэрокосмического приборостроения.docx
Добавлен: 12.12.2023
Просмотров: 10
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
КАФЕДРА № 41
ОТЧЕТ
ЗАЩИЩЕН С ОЦЕНКОЙ
ПРЕПОДАВАТЕЛЬ
| старший преподаватель | | | | Т.Н. Григорьева |
| должность, уч. степень, звание | | подпись, дата | | инициалы, фамилия |
| ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1 |
Моделирование работы детерминированного конечного автомата |
по курсу: Теория автоматов и формальных языков |
| |
| |
РАБОТУ ВЫПОЛНИЛ
| СТУДЕНТ ГР. № | 4616 | | | | А.В.Павлов |
| | | | подпись, дата | | инициалы, фамилия |
Санкт-Петербург 2018
1 СОДЕРЖАНИЕ
ЦЕЛЬ РАБОТЫ 2
ВАРИАНТ ЗАДАНИЯ 2
ХОД РАБОТЫ 3
ВЫВОД 8
2 ЦЕЛЬ РАБОТЫ
1. Получить у преподавателя индивидуальное задание.
2. В соответствии с логикой задания построить автомат Мили (составить входной и выходной алфавиты, определить алфавит состояний автомата, построить таблицу переходов-выходов)
3. Построить граф автомата Мили.
4. Минимизировать полученный автомат Мили
5. Построить автомат Мура, эквивалентный исходному.
6. Минимизировать полученный автомат Мура.
7. Промоделировать работу исходных автоматов и минимизированных автоматов,
протестировав их на одинаковых входных последовательностях
8. Сравнить полученные результаты, убедиться в эквивалентности их функционирования, сделать выводы.
3 ВАРИАНТ ЗАДАНИЯ
Вариант 9
| | Q0 | Q1 | Q2 | Q3 | Q4 | Q5 |
| a | Q2/x | Q0/y | Q4/x | Q4/y | Q4/x | Q1/x |
| b | Q1/y | Q5/x | Q1/y | Q5/x | Q3/y | Q0/y |
4 ХОД РАБОТЫ
Построим исходный автомат Мили
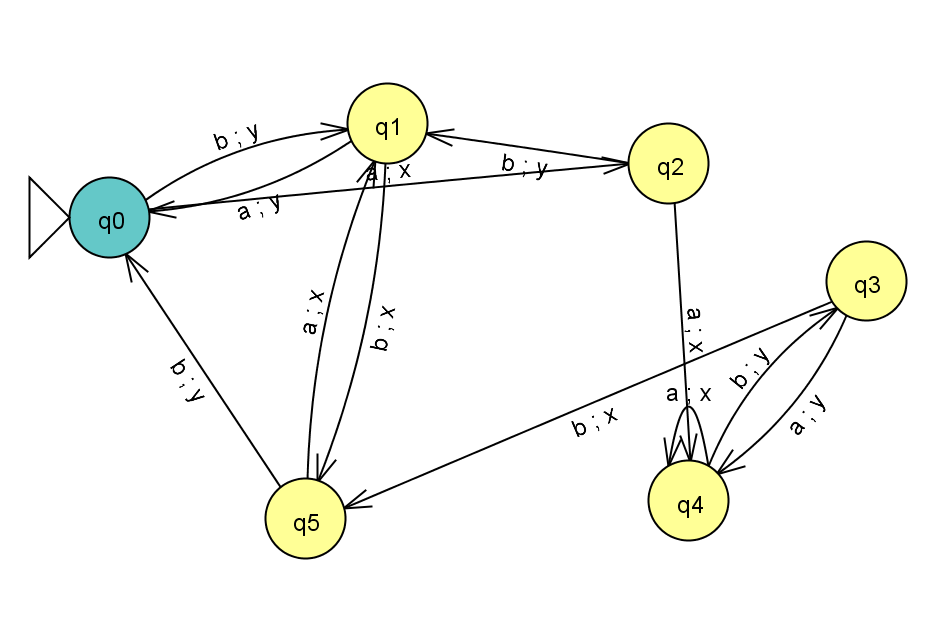
Рисунок 1 – Исходный автомат мили.
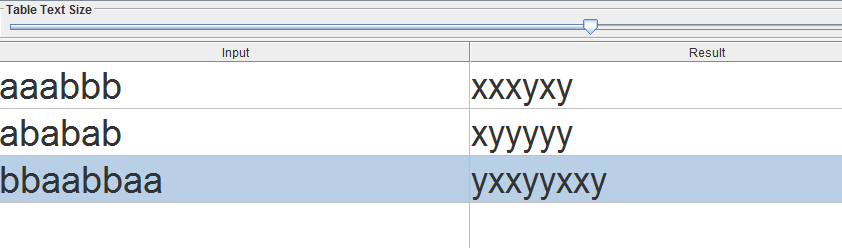
Рисунок 2 – Результат теста
Упросит автомат мили
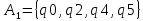
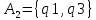
| | A1 | A2 | |||||
| | Q0 | Q2 | Q4 | Q5 | Q1 | Q3 | |
| a | A1 | A1 | A1 | A2 | A1 | A1 | |
| b | A2 | A2 | A2 | A1 | A1 | A1 | |
| | B1 | B2 | B3 | |||||
| | Q0 | Q2 | Q4 | Q5 | Q1 | Q3 | ||
| a | B1 | B1 | B1 | B3 | B1 | B1 | ||
| b | B3 | B3 | B3 | B1 | B2 | B2 | ||
| | C1 | C2 | C3 |
| a | C1/x | C3/x | C1/y |
| b | C3/y | C1/y | C2/x |
Получаем данный граф:
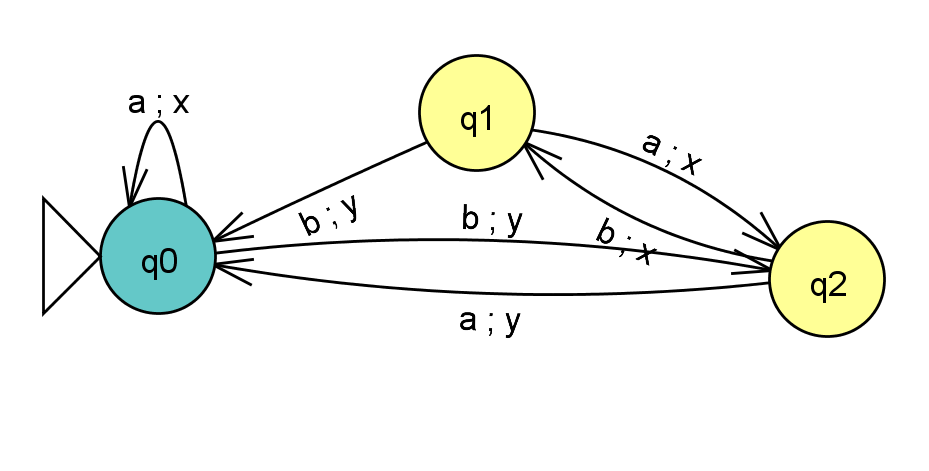
Рисунок 3 – Минимизированный граф Мили.
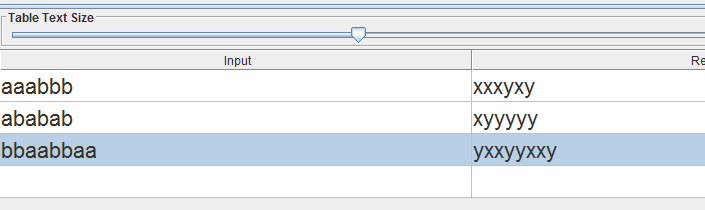
Рисунок 4 – Тест Графа
Строим автомат Мура по исходному заданию (1=x,2=y)
| | Q01/x | Q02/y | Q11/x | Q12/y | Q21/x | Q22/y | Q31/x | Q32/y | Q41/x | Q42/y | Q51/x | Q52/y |
| a | Q21 | Q21 | Q02 | Q02 | Q41 | Q41 | Q42 | Q42 | Q41 | Q41 | Q11 | Q11 |
| b | Q12 | Q12 | Q51 | Q51 | Q12 | Q12 | Q51 | Q51 | Q32 | Q32 | Q02 | Q02 |
Получаем такой граф
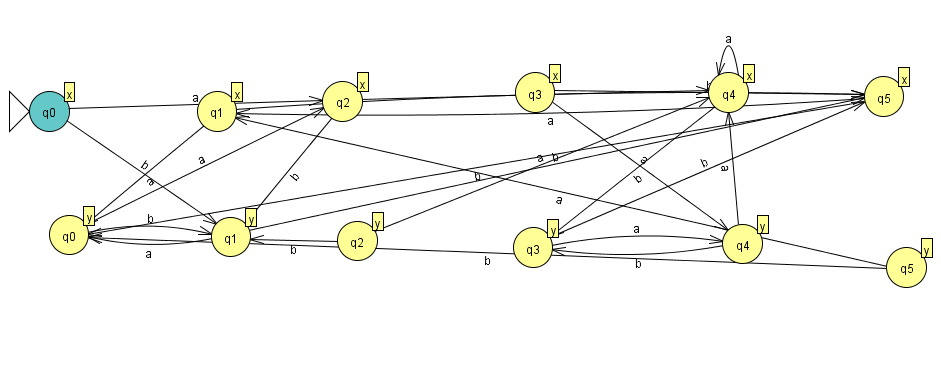
Рисунок 5 – Граф мура.
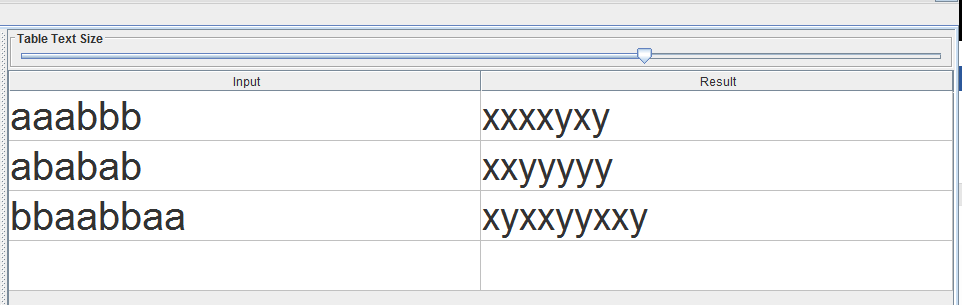
Рисунок 6 – Тест графа.
Путем долгих вычислений получим минимизированный автомат Мура.
| | Q01/x | Q02/y | Q11/x | Q12/y | Q21/x | Q22/y |
| a | Q01 | Q02 | Q21 | Q21 | Q02 | Q02 |
| b | Q22 | Q22 | Q02 | Q01 | Q11 | Q11 |
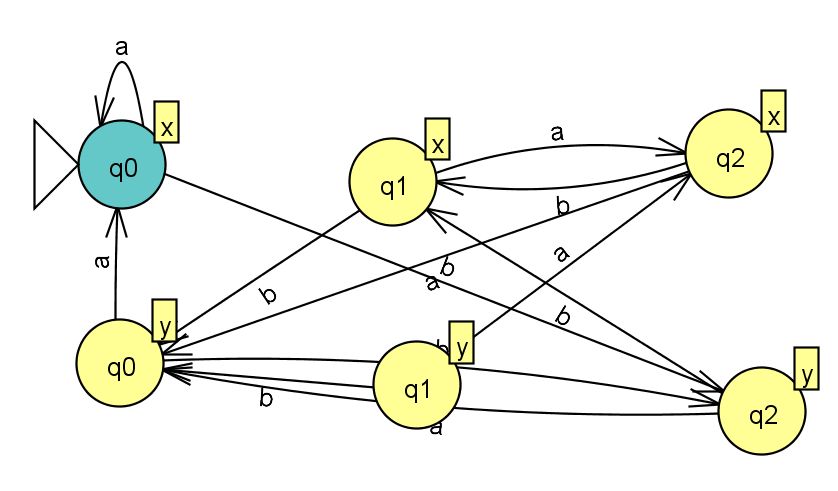
Рисунок 7 – Граф для минимизированного автомата Мура.
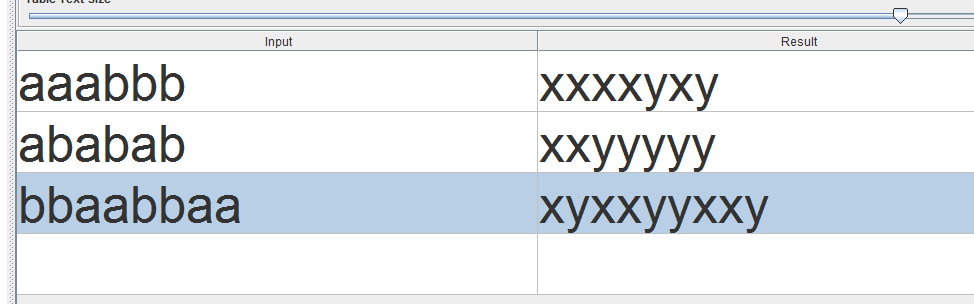
Рисунок 8 – Результат Теста.
Сравнение результатов тестов




Рисунок 10 – Сравнение Тестов.
ВЫВОД: В результате проделанной работы все графы сошлись в ответах, а это значит, что они эквиваленты, включая минимизированные графы.