Аңдатпа:Бұл мақалада 5-6 сыныптарға арналған мәтіндік логикалық есептердің кейбір түрлерінің әр түрлі тәсілмен шығару жолдары көрсетілген.Оқушылардың қабылдауы әр түрлі болғандықтан,есепті шешудің бірнеше тәсілін берген абзалырақ.Сондықтан мақалада логикалық есептердің шығарылуы екі немесе одан көп тәсілмен шешудің жолдары көрсетілген.Мақаланың негізгі мақсаты оқушыларды орташа және күрделі деңгейдегі есептерді шешуге қызығушылығын арттыру.

Аннотация:В этой статье показаны несколько способов решения логических задач для 5-6 классов.Из-за разного уровня восприятия учеников,предпочтительно преподносит несколько способов решения задач.По этому в статье решения логических задач происходят двумя и более методами.Основная цель статьи повысить интерес школьников к решению сложных задач.

Annotation: This article shows several ways to solve logical problems for grades 5-6. Due to the different level of perception of students, it is preferable to present several ways to solve problems. Therefore, two or more methods of solving logical problems are provided. The main goal of the article is to increase the interest of students in solving complex problems.

Кілт сөздер:Логикалық есептер,әдіс,5-6 сыныптар,шешу,әр түрлі.

Ключевые слова:Логические задачи,метод,5-6 классы,решать,разный.

Keywords: logical tasks,method,5-6 grades,solve,different

5-6 сыныптарға арналған кейбір логикалық есептерді шығару тәсілдері

Логикалық есептермен жұмыс істеу барысында баланың ойлау шапшаңдығы,ойлау қабілеттері дамиды.Ертеректе елімізде түрлі жұмбақ жасыру арқылы баланың ойлау қабілетін күшейтуге тырысқан.Қазіргі таңда ғылым мен техниканың тоқтаусыз қарқынды дамуы себепті біздің елімізге де ғылым мен техника бағытына бет бұрғанымыз абзал.Ғылым мен білімнің басы мектептен басталғандықтан,мектеп қабырғасынан болашақта ғылыммен айналысатын,не болмаса кез-келген мамандықты еш қиындықсыз меңгеретін алдыңғы қатарлы озат ұрпақ тәрбиелеуде логикалық есептердің,олимпиадалардың,зертханалық тәжірибелердің әсері мол.Айта кететін бір жәйт-қазақ тіліндегі логикалық-олимпиадылық есептердің аздығы және халықаралық немесе қалааралық олимпиадаларға дайындық тек арнайы мектептерде немесе жекелеген оқу центрлерінде ғана жүзеге асады.Еліміздің түпкір-түпкірінен логикалық есептерді шешуге қызығушылығы бар оқушыларға шабыт беру мақсатында жалпыға білім беретін мектептер үшін логикалық есептерді шешу жайлы мағлұматтың көбейгені жөн. Оны жүзеге асырудың бірден-бір жолы қосымша хрестоматия нұсқаулықтар шығару немесе мектепшілік демалысаралық уақытында үйірмелер ұйымдастыру.

---

Жалпы логикалық есептерді құрылымына,мазмұнына және қиындығына қарай деңгейлерге бөліп,әр түрлі деңгейдегі оқушыларға әр түрлі деңгеймен есептер беруге болады.Егер ұстаздарға нұсқаулық берген жағдайда мектептің жас мамандарының өзі көптеген логикалық есептерді шешуге оқушыларды үйрете алады.Мысал ретінде пайыздар тақырыбына қарапайым деңгейдегі келесі есепті қарастырып өтейік:

Мысал 1.Сүт 2 дүкенде де бірдей бағада еді,кейін бірінші дүкенде бірден 40%,ал екінші дүкенде алдымен 20%,кейін тағы 20% төмендеді.Енде қай дүкеннен сүт алған тиімді? Шешуі:

Сүттің алғашқы бағасын х деп аламыз

Бірінші дүкендегі сүттің бағасы x*0.6=0.6x

Екінші дүкендегі сүттің бағасы x*0.8*0.8=0.64x

Жауабы:Екінші дүкеннен сүт алу тиімдірек

Оқушылар әріппен шығаруға қиналған жағдайда,белгісіз айнымалы орнына ойдан сан алуға болады.Мысалы пайызбен шығатын есептерде 100 саны тиімді.Стандартты емес шешу жолы:

Осы есепке 100 санын дүкендегі сүттің алғашқы бағасы деп ойдан аламыз.

Бірінші дүкендегі сүттің бағасы 100*0.6=60

Екінші дүкендегі сүттің бағасы 100*0.8*0.8=64

Яғни логикалық есептерді шешу дағдысы енді қалыптасып келе жатқан оқушы үшін әр түрлі тәсілмен беру олардың толық түсіну ықтималдығын арттырады.Ойдан сан беріп есеп шығару әдісі стандартты емес есеп шығарудың көп әдістерінің бірі ғана болып табылады.

[П.В.Чулков,Арифметические задачи,издание пятое,стереотипное,МЦНМО,Москва,2015]

Мысал 2.Екі санның қосындысы 400 тең.Бірінші санды 20%,екінші санды 15% азайтса,олардың қосындысы 68-ге азаяды.азайғаннан кейінгі сандардың мәнін тап.

Бірінші әдіс:

x+y=400

0.8x+0.85y=332

Жүйені шеше отырып жауабын алады.

Екінші әдіс: 2 санды да тағы 5 есе кішірейтсек ,бірінші сан 100 % азаяды,яғни жойылады,екінші санның 35% қалады және қосынды 68*5 азаяды да,60-ты құрайды.0,25y=60;y=60/0.25=240

[Математикалық академия”, С.Полянских, Н.Хаджимуратов,В.Сосин.]
Яғни 1 әдісті көпшілік кең қолданып келеді әрі дәл 2 әдіс секілді дұрыс шешімін береді.Тек оқушының логикалық ойлау дағдыларына қарай қалағанымен шығаруға таңдау пайды болады.Жалпы 5-6 сыныптан кейін оқушылардың пәнге деген қызығушылығы класс жоғарылаған сайын жүйелі түрде азайып отырады.Оған деген қызығушылықты көтеру мақсатында логикалық есептерді әр түрлі тәсілдермен шығартып үйретуге болады.

Логикалық есептерді шығартып үйретуде тек есептерді түсіндірудің көпнұсқалылығы ғана емес,оқытудың көп жақтылығы да өзінің үлесін қосары сөссіз.Жалпы білім беретін мектеп бағдарламасында логикалық тақырыптарды толықтай кітапқа қосу қиынға туындағандықтан,оларды қосымша үйірме не тоқсанаралық демалыстар кезінде демалыс мектебін ұйымдастыру арқылы жүзеге асырып,пәнге қызығушылар қатарын көбейте аламыз.Мемлекет тарапынан қолдау көрсетілген жағдайда үйірмеге қатысып жүрген немесе мектепшілік демалыс уақытына арнап қосымша хрестоматия ретінде де шығару толық мүмкіндік бар.Дәстүрлі емес оқытуды қарапайым көбейтулерден де бастаса болады.Айталық,жапондар мен қытайлар көбейту бағанмен емес сызықтар арқылы жүзеге асырады және қытай елінің оқушылары есеп шығаруға сабақтың шамамен 30% уақытын ғана құртады екен.Қалған уақытын бүкіл сыныпқа арналған интерактивті тапсырмаларға уақыт арнайды.Европаның кейбір елдері сабақ үстінде ақпараттық құрылғы мен техникаларды толық қолдануға мүмкіндік береді.Логикалық есептерді дәстүрлі емес шешудің жолдары көп,солардың ішінді:

---

• 
  Талқылау әдісі
  
• 
  Кестелер әдісі
  
• 
  Алгебралық әдіс
  
• 
  Графтар әдісі
  
• 
  Логикалық өрнектерді түрлендіру әдісі
  
• 
  Және т.б. көптеген әдістер
  

Бұл әдістер олимпиадалық немесе конкурстық есептер сайысында көптен бері қолданылып келуде.Алайда жалпы білім беретін мектептерде бұл әдістер сирек қолданғандықтан,жалпы білім беретін мектептер үшін бұл әдістерді аздап енгізу оқушылар үшін мотивацияның жаңа түрі болуы әбден мүмкін.Илон Маск,Стив Джобс немесе Павел Дуров секілді жаңа таланттар осы біздің еліміздің оқушыларынан шығу үшін,олардың мықты жақтарын байқау үшін біз білім мен ғылымды ең көркем түрде беруіміз қажет.
Бұл әдістердің көмегімен де бір есепті екі не одан да көп әдістермен шығару мүмкіндігі туындайды.Келесі есепте бұған көз жеткіземіз.

Мысал 3.

Метрода сыныптас 5 оқушы Алмас,Бекжан,Дамир,Ерасыл және Ғалым жалғыз отырған профессормен танысады.Танысу барысында сыныптастар профессорға олардың жөндерін тауып көруге ұсыныс жасады.Алайда олар бір шын тұжырым және бір жалған тұжырым жасады.

Дамирдың айтқаны:”Менің жөнім –Мирасұлы,ал Бекжандікі -Оспанов.

Алмастың айтқаны:”Мирасұлы –менің жөнім,Ерасылдікі-Бақберген”

Бекжанның айтты:”Ерасылдың жөні –Тоқтаров,ал менікі Мирасұлы”

Ерасылдың айтқаны:”Менің жөнім-Бақберген,ал Ғалымның жөні-Шоңов”

Ғалымның айтқаны:”Ия,менің жөнім Шоңов,ал Алмастікі-Тоқтаров”

Сыныптастардың жөндерін табыңыз.

Талқылау әдісіне кезек берейік.Айталық,Дамирдің эөні Молотов болсын,онда Алмас пен Бекжанның жөндері басқа.Бірақ олардың жөндері басқа болса,Ерасыл Бақберген мен Ерасыл Тоқтаровтың жөндері дұрыс табылған.Алайда Ерасыл біруақытта Бақберген мен Тоқтаров бола алмайды.Нәтижесінде бізде бір шындыққа ұқсайтын жағдай қалады,Бекжан-Оспанов.Бекжан Оспанов шын болса,Бекжан Мирасұлы жалған.Ерасыл Тоқтаров -шын,Алмас Шоңов-жалған. Ғалым Шоңов-шын,Ерасыл Бақберген –жалған және Алмас Мирасұлы-шын.

Жауабы:Бекжан-Оспанов,Ерасыл Тоқтаров,Ғалым Шоңов,Алмас Мирасұлы,Дамир Бақберген.Есеп шықты,әдіс тиімді,тек барлық оқушыларға емес.Оқушылардың көбі мағлұмат көбейіп кеткен жағдайда шатаса бастайды.Сондықтан келесі әдіс кестелер әдісі.Бұл жерде талқылау қанша көп болса да барлығы оқушының көз алдында.

	Алмас	Бекжан	Ерасыл	Дамир	Ғалым
Оспанов	-	+	-	-	-
Тоқтаров	-	-	+	-	-
Шоңов	-	-	-	-	+
Мирасұлы	+	-	-	-	-
Бақберген	-	-	-	+	-

---

Яғни оқушы әр қадам сайын бола алатын және бола алмайтын үміткерді сызып не белгілеп қою арқылы белгісіздер санын азайтып отырады.

Кей оқушылар есептің суретін салу арқылы есепті оңай шығарады.Оны үйретудің бір мысалын келесі есепте қарастырайық:

[Нагибин Ф. Ф., Канин Е. С. Математическая шкатулка. – М.: Дрофа, 2006. – 270 с.]

Мысал 4.

7 рет қолданылғаннан кейін сабынның ұзындығы,ені мен биіктігі екі есе қысқарды.Сабынды енді қанша рет қолданса болады?
Шешуі:Ұзындығын а,енін b.ал биіктігін с деп белгілейік.Барлық өлшемдері екі есе кішірейгендіктен,қалған көлемі 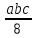.abc-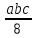 = 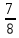abc.Яғни,барлығы 8 мәрте жууға жетеді.Сондықтан қалғаны 1 жуу.Жауабы:1 рет қолданысқа жетеді
5,6 сынып оқушылары көлем ұғымында қиыншылықтар болуы мүмкін,сол себепті салу әдісіне көңіл бөлу ықтималдықты арттырады.Енді осы есепті салу әдісімен шығарсақ,



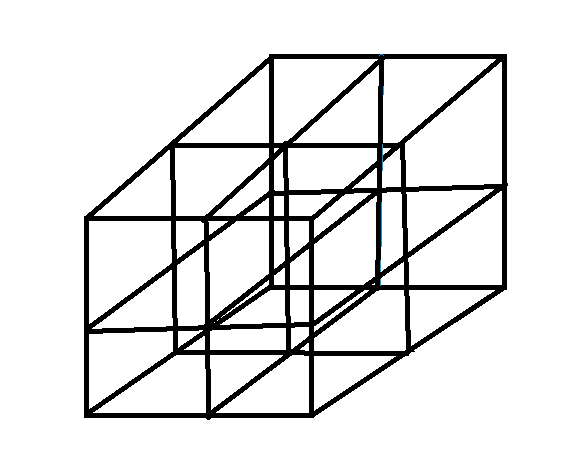
Байқасаңыздар,сабын 8 бөлікке бөлінді,7 бөлігін қолданып қойсақ қалғаны 1 бөлік.

[А.В.Спивак,Тысяча и одна задача по математике,6-ое издание.Москва,2016]

Мысал 5

Аулада сиырлар мен тауықтар жүр.Олардың бастарының қосындысы 10,аяқтарының қосындысы 28.Аулада қанша сиыр,қанша тауық жүр?

Шешуі,1 әдіс:

Сиырларды <х> деп,ал тауықтарды <у> деп белгілейік.Сонда х+у=10.Сиырда 4 аяқ,ал тауықтарда 2 аяқтан.Сонда 4х+2у=28

Яғни келесі жүйені шешеміз:

x+y=10

4x+2y=28.Жүйені шеше отырып x=4,y=6 екеніне көз жеткіземіз.

2 тәсіл: Барлық жануардан екі-екі аяқтан кесіп тастайық.Сонда тауықтарда аяқ қалмайды,ал сиырларда екі-екі аяқтан қалады.10 жануардан 20 аяқ кесілді,қалғаны 8 аяқ және ол әр сиырда екіден қалды.8/2=4.Демек,4 сиыр бар,ендеше 6 тауық бар.

[сайт https://ped-kopilka.ru/blogs/krjazhevskih-elena/reshenie-zadach-golovy-i-nogi.html,дата обращения 10.10.2021]

6 мысал. Ермек 12 жаста,ал оның ұстазы 42 жаста.Қанша жылдан кейін ұстазы Ермектен 2 есе үлкен болады?

Шешуі:

1 тәсіл.Ермекке қанша жыл өтсе,ұстазына да сонша жыл өтеді.Яғни белгілі быр жыл өтіп,екіге көбейтсек ұстаздың жасы шығуы тиіс.

(12+x)*2=42+x

Теңдеуді шеше отырып х=18 екенін анықтаймыз.

2 тәсіл:Қазір екеуінің жас айырмашылығы 30,ал егер олардың жас айырымынан кішісінің жасын алсақ,қанша уақыттан кейін олардың жас айырымы 2 есе болатынын көрсетеді.Себебі кішісінің жасын екі рет азайтқандықтан кішісінің жасы екі рет қолданылды.

---

42-12=30,
30-12=18

[А.В.Спивак,Тысяча и одна задача по математике,6-ое издание.Москва,2016]

Мысал 7.Иван,Дмитрий және Степан Мәскеу,Тула және Новогород қалаларында әр түрлі пәндерден сабақ береді(химия,физика,биология).Олар туралы келесі мәліметтер белгілі:

Иван Мәскеуде жұмыс істемейді,Дмитрий Новгорода сабақ бермейді.

Мәскеулік физикадан сабақ береді.

Новгородта жұмыста жүрген мұғалім химиядан сабақ береді.

Дмитрий мен Степан биолог емес.Кім қай қалада қандай пәннен сабақ береді?

Шешуі:

Тәсіл 1:Кестелер әдісі.Бұл есепте қаладан бөлек пәндер болғандықтан,екі кесте құрамыз.

	Химия	Биология	Физика
Иван	-	+	-
Дмитрий	-	-	+
Степан	+	-	-

	Мәскеу	Новгород	Тула
Иван	-	-	+
Дмитрий	+	-	-
Степан	-	+	-

2 тәсіл: Анализ әдісі.Дмитрий мен Степан биолог емес,яғни биолог Иван.Химия мұғалімі Новгородта,ал Физика мұғалімі Мәскеуде тұратыны белгілі.Ендеше биолог Туланікі.Яғни Иван-Туланікі.Дмитрий Новгородта сабақ бермейді,ал Тулада Иван.Демек,Дмитрий Мәскеулік және физикадан сабақ береді.Бұдан шығатыны Степан Новгородта химиядан сабақ береді.

3 тәсіл:Графтар әдісі


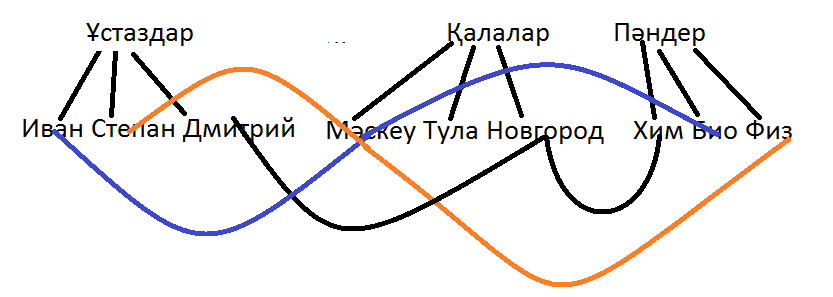
Есептің берілгені бойынша Иван мен Мәскеді,Дмитрий мен Новгородты қосамыз.Келесісі Физик пен Мәскеуді қосамыз.Есептің шарты бойынша Новгород пен Химияны қосамыз.Дмитрий мен Степан биолог емес,яғни Иван Мәскеу арқылы биологиямен қосамыз

[Журнал «Математика в школе», № 3, 2005, стр. 32]
Логикалық есептерді 5-6 сыныптарға көбейту-алғашқы орында болмаса да қарқынды даму жолында өзекті мәселелердің бірі болып табылады әрі оны шешу-тек біздің қолымызда.Стандартты есептерден логикалықтарға ауысып отыру оқушыны қосымша білім алуға итермелеуі сөзсіз.

---

Смотрите также файлы

• Кні Ж.изатов атындаы 23 мектеплицей.docx

• Сценарий школьной научнопрактической конференции. Жас зерттеуші.docx

• Диссертация ылыми жетекшісі п.. к., ауым проф м. а. М. Т. Искакова орауа жіберілді.docx

• Создание нажмите кнопку Пустая форма. Откроется пустая форма в режиме макета, и отобразится область Список полей.docx

• Кружок Занимательная математика.pptx