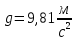Файл: Отчет по лабораторной работе 3 определение ускорения свободного падения при помощи универсального маятника.docx
Добавлен: 12.12.2023
Просмотров: 165
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное государственное бюджетное образовательное учреждение высшего образования
Санкт-Петербургский горный университет
КАФЕДРА ОБЩЕЙ И ТЕХНИЧЕСКОЙ ФИЗИКИ
ОТЧЕТ
по лабораторной работе № 3
«ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ ПРИ ПОМОЩИ
УНИВЕРСАЛЬНОГО МАЯТНИКА»
| Выполнил: студент гр. ТПР-22 | __________ | / Трунов С.Д. / | |
| (шифр группы) | (подпись) | (Ф.И.О) | |
| Проверил: | | __________ | / / |
| | (должность) | (подпись) | (Ф.И.О.) |
Санкт-Петербург
2023
1. ЦЕЛЬ РАБОТЫ
Определить ускорение свободного падения при помощи универсального маятника.
2. КРАТКОЕ ТЕОРЕТИЧЕСКОЕ СОДЕРЖАНИЕ
Явление, изучаемое в работе. Зависимость периода колебаний универсального маятника от ускорения свободного падения.
Определения физических понятий, объектов, процессов и величин.
Математическим маятником называется материальная точка, подвешенная на невесомой, нерастяжимой нити и совершающая колебание в вертикальной плоскости под действием силы тяжести.
Физическим маятником называется абсолютно твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр тяжести.
Ускорение свободного падения – это физическая величина, численно равная отношению силы, действующей на тело со стороны гравитационного поля, к его массе.
Период колебаний – наименьший промежуток времени, за который колебательная система возвращается в первоначальное состояние.
Приведенная длина физического маятника – длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.
Законы и соотношения, описывающие изучаемые процессы, на основании которых получены расчетные формулы. Пояснения к физическим величинам и их единицам измерения.
Период математического маятника [с]:
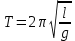
где l – длина маятника [м]; g – ускорение свободного падения [м/с2].
Период колебаний физического маятника [с]:
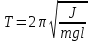
где J – момент инерции маятника относительно оси качаний [кг·м2]; m – его масса [кг]; l – расстояние от центра масс до оси качаний [м]; g – ускорение свободного падения [м/с2].
Приведенная длина физического маятника [м]:
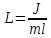
где J – момент инерции маятника относительно оси качаний [кг·м2]; m – его масса [кг]; l – расстояние от центра масс до оси качаний [м].
Метод оборотного маятника основан на том, что во всяком физическом маятнике можно найти такие две точки, что при последовательном подвешивании маятника за одну или другую, период колебаний его остается одним и тем же.
Расстояние между этими точками представляет собой приведенную длину данного маятника [м]:
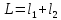
Допустим, что нам удалось найти такое положение грузов, при котором периоды колебаний маятников Т1 и Т2 совпадают:
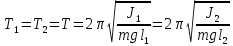
Отсюда следует, что:
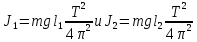
По теореме Штейнера:
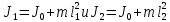
где J0 - момент инерции маятника относительно оси, проходящей через его центр масс и параллельной оси качаний.
С учетом формул можно записать:
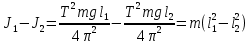
Следовательно:
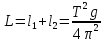
где L – приведенная длина физического маятника [м]; l1 и l2 – длины маятников для двух грузов [м]; T – период физического маятника [с]; g – ускорение свободного падения [м/с2].
3. СХЕМА УСТАНОВКИ
1
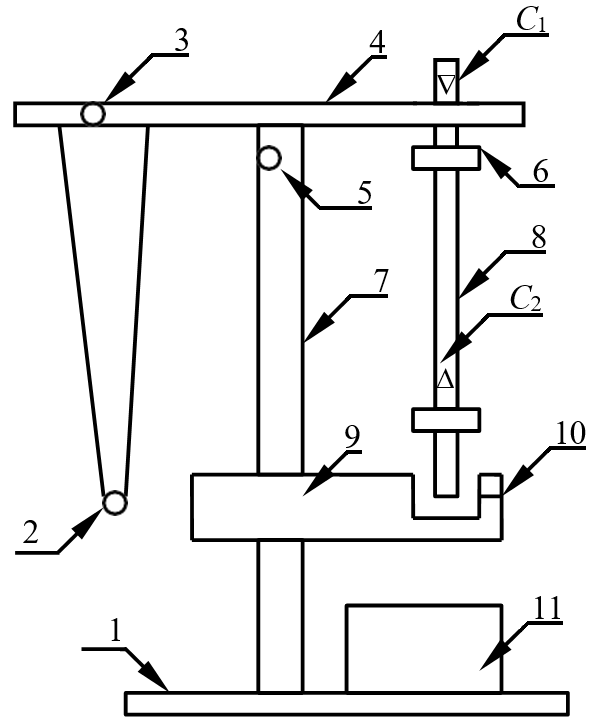) Основание универсального маятника;2) Математический маятник;
3) 5) Винты;
4) Верхний кронштейн;
6) Диски;
7) Колонка;
8) Оборотный маятник;
9) Нижний кронштейн;
10) Фотоэлектрический датчик;
11) Секундомер
C1 и C2 – призмы.
4. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Период маятника [с]:
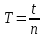
где t – время колебаний [с]; n – количество полных колебаний.
Ускорение свободного падения для математического маятника [м/с2]:
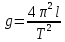
где T – период математического маятника [с]; l – длина маятника [м].
Ускорение свободного падения для физического маятника [м/с2]:
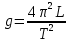
где T – период физического маятника [с];
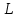– приведенная длина физического маятника [м].5. ФОРМУЛЫ ДЛЯ РАСЧЕТА ПОГРЕШНОСТЕЙ КОСВЕННЫХ ИЗМЕРЕНИЙ
Формулы для расчета погрешностей косвенных измерений:
Абсолютная погрешность косвенных измерений периода маятника [с]:
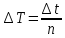
где
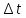– погрешность измерений времени колебаний [с]; 
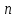– количество колебаний.Абсолютная погрешность косвенных измерений ускорения свободного падения для математического маятника:
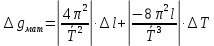
где
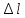– погрешность измерения длины маятника [м]; 
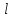– длина маятника [м]; 
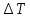– абсолютная погрешность косвенных измерений периода маятника [с]; 
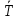– средний период колебаний математического маятника [с].Абсолютная погрешность косвенных измерений ускорения свободного падения для физического маятника:
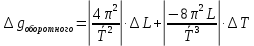
где
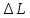– погрешность измерения приведенной длины маятника [м]; 
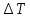– приведенная длина маятника [м]; – абсолютная погрешность косвенных измерений периода маятника [с]; 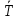– средний период колебаний маятника [с].6. ТАБЛИЦЫ И ВЫЧИСЛЕНИЯ
Таблица 1
Математический маятник
| Номер опыта | t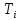,c |  ,c | 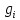 | l,м |
| 1 | 14,334 | 1.4334 | 9,559030 | 0.498 |
| 2 | 14,334 | 1.4334 | | |
| 3 | 14,341 | 1.4341 | | |
| 4 | 14,340 | 1.4340 | | |
| 5 | 14,341 | 1.4341 | | |
| 6 | 14,339 | 1.4339 | | |
| 7 | 14,345 | 1.4345 | | |
| 8 | 14,344 | 1.4344 | | |
| 9 | 14,340 | 1.4340 | | |
| 10 | 14,343 | 1.4343 | |
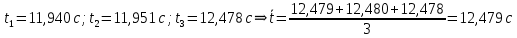
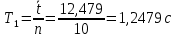
Для призмы С2:
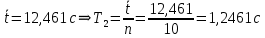
Точность равенства
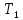и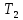 
:
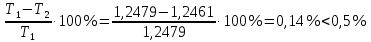
Исходные данные:
Длина математического маятника l = 0,408 м; число π= 3,1416; количество колебаний за измерение n = 10; приведенная длина физического маятника L= 0,392 м.
Пример вычислений:
Математический маятник
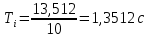
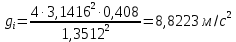
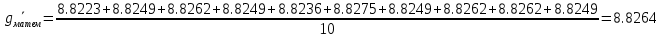
Оборотный маятник
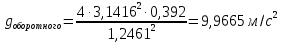
Погрешности прямых измерений:
; 
; 
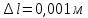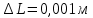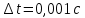. Погрешности косвенных измерений:
Абсолютная погрешность косвенных измерений периода маятника:
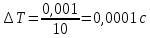
Абсолютная погрешность косвенных измерений ускорения свободного падения для математического маятника:
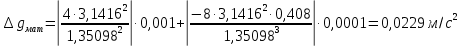
Абсолютная погрешность косвенных измерений ускорения свободного падения для физического маятника:
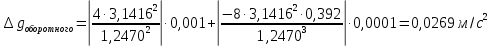
7. РЕЗУЛЬТАТ И ВЫВОД
В ходе данной лабораторной работы были проделаны вычисления ускорения свободного падения при помощи универсального маятника. Для математического маятника среднее значение составило
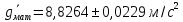, а для оборотного маятника 
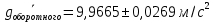. Данные значения сходятся межу собой с высокой точностью 
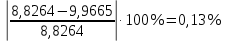и близки к общепринятому значению ускорения свободного падения 