Файл: Контрольная работа по дисциплине Теория автоматического управления Задание 1.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Приведем без доказательства формулировку критерия Гурвица. Пусть дано характеристическое уравнение замкнутой системы
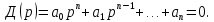 | |
Прежде всего проверяется необходимое условие устойчивости —
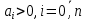 . Если оно не выполняется, то система не является асимптотически устойчивой.
. Если оно не выполняется, то система не является асимптотически устойчивой.При выполнении данного условия составляется матрица Гурвица по следующему
правилу.
По главной диагонали последовательно выписывают коэффициенты
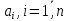 характеристического многочлена начиная с
характеристического многочлена начиная с 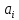 . Вниз от элементов главной диагонали столбцы заполняют коэффициентами
. Вниз от элементов главной диагонали столбцы заполняют коэффициентами 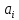 с последовательно убывающими
с последовательно убывающимииндексами и нулями, когда индексы становятся отрицательными. Вверх от главной
диагонали столбцы заполняются коэффициентами
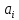 с возрастающими индексами
с возрастающими индексамии нулями, когда индекс должен бы быть больше n. Строки матрицы состоят из
коэффициентов
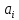 либо только с нечетными, либо только с четными индексами и
либо только с нечетными, либо только с четными индексами инулями:
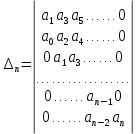 .
.Критерий Гурвица гласит: система устойчива, если при
 > 0 главный определитель Гурвица и все его диагональные миноры
> 0 главный определитель Гурвица и все его диагональные миноры 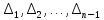 положительны, причем
положительны, причем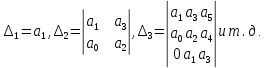
Если главный определитель
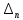 равен нулю, то система находится на границе
равен нулю, то система находится на границеустойчивости. Так как
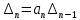 , то возможно два случая:
, то возможно два случая:В первом случае говорят об апериодической границе устойчивости, во втором — о колебательной границе устойчивости.
-
Расчетная часть
2.1 Задание на контрольную работу
-
Определить передаточные функции системы и составить дифференциальное уравнение, связывающее выходной сигнал системы с внешними воздействиями. -
Исходя из заданной точности определить желаемый коэффициент усиления системы и коэффициент усиления усилителя. -
По критерию Гурвица определить устойчивость системы при значении коэффициента усиления системы, полученного в п.2. -
Построить ЛАЧХ неизменяемой части системы.
Система автоматической установки масштабных коэффициентов в аналоговом вычислительном комплексе.
При ручной установке масштабных коэффициентов неизбежны субъективные ошибки. Для уменьшения величины ошибок и увеличения скорости установки масштабных коэффициентов применяется автоматическая система, имеющая структурную схему, показанную на рисунке 4.

Рисунок 4 – Структурная схема системы
Система работает следующим образом. С помощью клавишного устройства на вход следующей системы подается напряжение
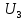 , пропорциональное требуемому углу
, пропорциональное требуемому углу 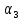 поворота настраиваемого потенциометра. Оно сравнивается напряжением
поворота настраиваемого потенциометра. Оно сравнивается напряжением 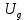 , пропорциональным действующему углу
, пропорциональным действующему углу 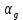 – поворота настраиваемого потенциометра. Напряжение
– поворота настраиваемого потенциометра. Напряжение 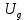 снимается с потенциометрического преобразователя
снимается с потенциометрического преобразователя 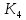 .
.При отклонении угла
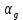 от угла
от угла 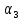 напряжение рассогласования
напряжение рассогласования 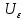 , проходя по прямой цепи управления, состоящей из модулятора
, проходя по прямой цепи управления, состоящей из модулятора 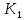 , усилителя переменного тока с передаточной функцией
, усилителя переменного тока с передаточной функцией 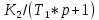 вызывает поворот вала настраиваемого потенциометра до полного устранения рассогласования.
вызывает поворот вала настраиваемого потенциометра до полного устранения рассогласования.
Исходные данные и требования к системе:
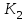 = 3 = 3 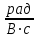 | , |
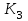 = 4 = 4 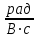 | , |
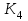 = 0,01 = 0,01 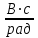 | , |
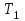 = 0,015 с = 0,015 с | , |
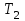 = 0,07 с = 0,07 с | , |
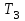 = 0,15 с = 0,15 с | , |
| Еск = 0,6 град | , |
| x(t)=v·t v=40град/с. | |
-
Определение передаточных функций системы и составление дифференциального уравнения, связывающего выходной сигнал системы с внешними воздействиями
Передаточная функция разомкнутой системы определяется по формуле (1):
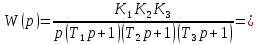
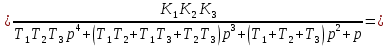
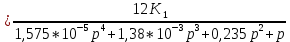
Передаточную функцию замкнутой системы находим по формуле (2):
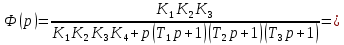
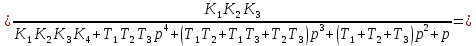
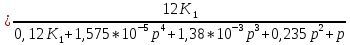
Передаточную функцию замкнутой системы по возмущению определим по формуле (3):
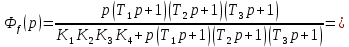
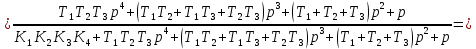
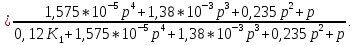
Передаточную функцию замкнутой системы по ошибке находим по формуле (4):
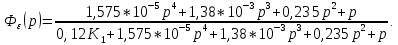
Составим дифференциальное уравнение замкнутой системы. Для этого сперва запишем уравнение замкнутой системы в изображениях:
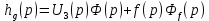 =
=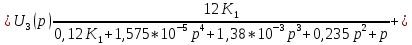
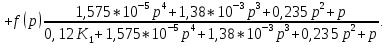
Перенесем знаменатель в левую часть:
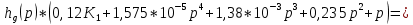
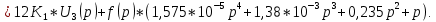
Теперь перейдём от изображений к оригиналам. Чтобы осуществить этот переход, у в левой части выражения произведём замену
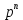 на
на 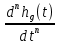 ,а в правой – на
,а в правой – на 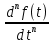 :
: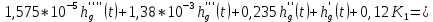
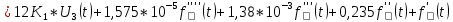
2.3 Определение желаемого коэффициента усиления системы и коэффициента усиления усилителя исходя из заданной точности
Исследуемая система является системой первого порядка астатизма со входным сигналом вида:
v(t) =
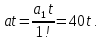
В данном случае установившаяся ошибка вычисляется по формуле (6). Из неё
найдём желаемый коэффициент усиления всей системы:
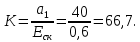

Теперь найдём коэффициент усиления усилителя
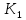 :
: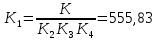
ПФ разомкнутой системы:
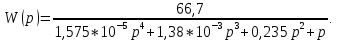
ПФ замкнутой системы:
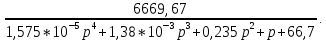
2.4 Определим по критерию Гурвица устойчивость замкнутой системы при значении коэффициента усиления, полученного в п.2
Характеристическое уравнение нашей системы имеет вид:
А(p) =
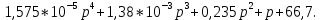
Прежде чем строить матрицу Гурвица, проверим необходимое условие устойчивости: все коэффициенты
 , i = 0,n характеристического уравнения должны быть больше нуля. Все коэффициенты
, i = 0,n характеристического уравнения должны быть больше нуля. Все коэффициенты  , больше нуля.
, больше нуля.Составим матрицу Гурвица для уравнения:
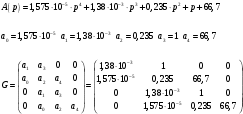
Найдем определители этой матрицы:
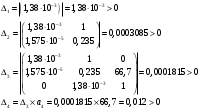
Определители всех 4 порядков положительные; замкнутая система устойчива.
2.5 Построение ЛАЧХ разомкнутой системы
График частотных характеристик системы построим при помощи системы
MATLAB:
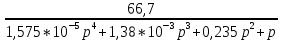

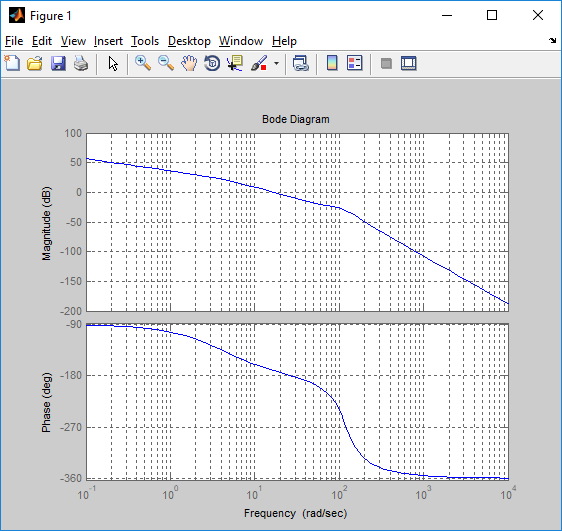
Рисунок 4 - ЛАЧХ разомкнутой системы
По полученным частотным характеристикам видим, что система устойчива, т.к. на частоте среза ЛАЧХ значение ЛФЧХ составляет: φ(ω) > –180º.
Построим годограф Найквиста разомкнутой системы:
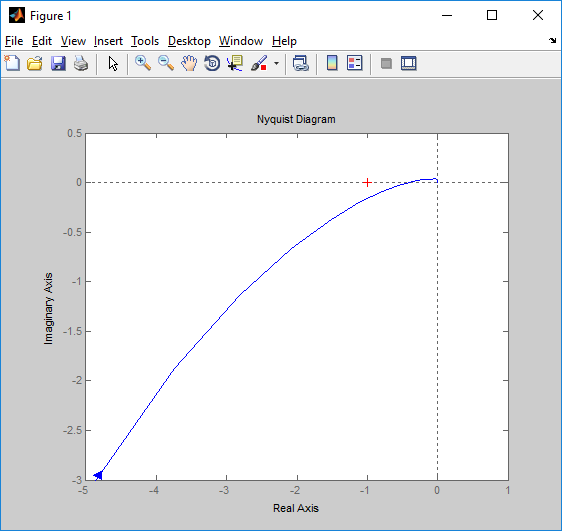
Рисунок 5 – Годограф Найквиста разомкнутой системы
Из критерия Найквиста следует, что система устойчива, т.к. АФХ не охватывает критическую точку (-1, j0).
Список используемых источников
-
Воронов А.А.: Теория автоматического управления, Москва: издательство Высшая школа, 1986. — 367 с, ил. -
Афанасьев, Калмановский, Носов: Математическая теория конструирования систем управления, Москва: издательство Высшая школа, 2003. — 615 с. -
Певзнер Л.Д.: Теория систем управления, Москва: Издательство Московского государственного горного университета 2002. – 472 с. -
Шишмарев В.Ю.: Основы автоматического управления, Москва: издательство Академия, 2008. – 347 с.