Камеральная обработка теодолитной съемки

Вычисление координат точек теодолитного хода

Вычисление координат производится в ведомости стандартной формы, образец которой приведен в Приложении 1.

В колонки I и 14 вписывают номера (названия) исходных пунктов полигонометрии и точек теодолитного хода по порядку в соответствии с абрисом (рисунок 1); в колонку 2 - измеренные горизонтальные углы β (таблица 1); в колонку 3 - исходные дирекционные углы: начальной стороны (α_41-42) и конечной стороны (α_46-47) красным цветом; в колонки 13 и 14 координаты X и Y начальных точек (пп42 и пп41) и конечных точек (пп46 и пп47) красным цветом.

Таблица 2 – Координаты исходных пунктов

Номер пункта полигонометрии	Прямоугольные координаты, м
	X	Y
41	231,72	141,97
42	131,71	61,93
46	251,86	381,84
47	361,87	287,82

Примечание:

Дирекционный угол начальной стороны α_41-42 = 218^˚40^΄30^˝,

дирекционный угол конечной стороны α _46-47 =317^˚43^΄30^˝.

Составление схемы теодолитного хода. Для наглядности и для исключения грубых ошибок вычислений с абриса (рисунок 1) в колонке 15 вычерчивают схему хода, где указывают исходные пункты полигонометрии, точки теодолитного хода 1,2,3 и результаты измерений горизонтальных углов и длин линий между точками теодолитного хода.
Предварительное (приближенное) вычисление дирекционных углов. Приближенное значение дирекционных углов вычисляют по формуле:

α_посл= α_пред – 180^˚ + β_лев,

где α_посл – дирекционный угол последующей стороны;

α_пред - дирекционный угол предыдущей стороны;

β_лев - измеренный горизонтальный угол, левый по ходу.

Дирекционные углы должны быть в пределах от 0^˚ до 360˚, поэтому при необходимости к полученному результату прибавляют 360˚.

Вычисление приближенных дирекционных углов производят в следующем порядке:

---

α_41-42 = 218^˚40^΄30^˝;

α_42-1 = α_41-42 + β₄₂ ± 180^˚ = 218^˚40^΄30^˝ + 86^˚19^΄00^˝ – 180^˚ = 124^˚59^΄30^˝

α_1-2 = α_42-1 + β₁ ± 180^˚= 124^˚59^΄30^˝ + 149^˚05^΄00^˝ – 180^˚ = 94^˚04^΄30^˝

α_2-3 = α_1-2 + β₂ ± 180^˚= 94^˚04^΄30^˝ +90^˚18^΄30^˝–180^˚ = 4^˚23^΄00^˝

α_3-46 = α_2-3+β₂ ±180^˚= 4^˚23^΄00^˝ + 220^˚35^΄30^˝ – 180^˚ = 44^˚58^΄30^˝

α_46-47 = α_3-46 + β₄₆ ± 180^˚ = 44^˚58^΄30^˝ + 92^˚44^΄30^˝ + 180^˚ = 317^˚43^΄00^˝

Определение угловой невязки. Угловую невязку ƒ_β вычисляют по формуле:

ƒ_β = α_{46-47прак} - α_{46-47теор},

где α_{46-47теор} – дирекционный угол конечной стороны, выписанный из таблицы 2.

α_{46-47прак} – приближенный дирекционный угол линии.

Для рассматриваемого варианта имеем:

ƒ_β= 317^˚43^΄00^˝ - 317^˚43^΄30^˝ = -30^˝

Допустимость угловой невязки проверяют по формуле:

ƒ_{β доп}= ± 2τ^˝ ,

где n – число углов в ходе,

τ - точность отсчетного приспособления прибора.

Для τ = 30^˝

ƒ_{β доп} = ± 2 × 30^˝ = 2^΄14^˝

Вычисленная невязка ƒ_β должна удовлетворять условию:

| ƒ_β |≤ | ƒ_{β доп} |.

В данном случае

|−30^˝| ≤ 2^΄14^˝.

На практике, если это условие не выполняется, то измерения горизонтальных углов повторяют. Обучающийся в этом случае должен проверить правильность вычислений углов или обратиться к преподавателю. Все расчёты по определению угловой невязки помещают в колонку 16 ведомости.

Распределение угловой невязки. Вычисленную угловую невязку распределяют с обратным знаком поровну на все измеренные углы:

υ_β= − ƒ_β ⁄ n = −30^˝ ⁄ 4= 7,5^˝,

где υ_β – поправка в измеренные горизонтальные углы.

На практике, если поправка υ_β меньше точности измеренного угла τ˝, целесообразно округлять её до величин, равной τ˝, но значение n×υ_β при этом должно быть равно величине невязки с обратным знаком: υ

---

_β=−ƒ_β.

Поправку записывают в колонку 2 ведомости координат над значением угла, в который вводится поправка υ_β. При этом в первую очередь поправка вводится в измеренные углы, прилегающие к коротким сторонам.

В рассмотренном варианте угловую поправку, равную +30^˝, вводят в измеренный угол на вершине 3 (поправка записывается красным цветом).
Вычисление уравненных дирекционных углов и румбов (табличных углов).

Уравненные дирекционные углы подсчитываются по тем же формулам, что и приближенные, но измеренные углы берут с учетом поправок υ_β.

Например: β_46(испр)= 220^о35^/30^// + 30^// = 220^о36^/00^//

Уравненные дирекционные углы записывают в колонку 4 ведомости, контролем является получение точного значения дирекционного угла конечной стороны – α_46-47.

По уравненным дирекционным углам вычисляют табличные углы согласно схеме (рисунок 2). На схеме: индексы 1, 2, 3, 4 указывают соответственно номер четверти в декартовой левой системе координат; r – румбы; α- дирекционные углы.

Вычисленные румбы записывают в колонку 4 ведомости под соответствующим дирекционным углом.



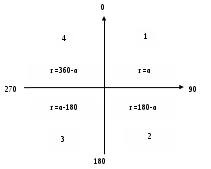
Рисунок 2 - Схема вычисления румбов
Вычисление горизонтальных проложений линий.

Горизонтальные проложения d вычисляются по формуле:

d = D× cos ν

где D - среднее значение измеренной длины линии,

ν – угол наклона.

Для стороны теодолитного хода D_1-2 = 140,39м; ν = 2^о34^/.
d = D_1-2 × cos 2^о34^/ = 140,39 × 0,998997 = 140,2м
Вычисленные горизонтальные проложения записываются в колонку 6 ведомости.

Определение приращений координат. Приращения координат Δx и Δy определяют по формулам:

Δx = d × cos α

Δy = d × sin α

При наличии вычислительной техники, позволяющей находить значения тригонометрических функций, вычисление румбов не обязательны. При традиционном способе вычисления производят по формулам:

Δx = d × cos r

Δy = d × sin r

Знаки приращения координат определяют в соответствии с четвертью дирекционного угла согласно схеме (рисунок 3), значения cos r и sin r определяют по калькулятору.


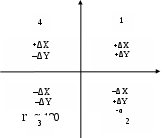
Рисунок 3 - Схема определения знаков приращений координат
Приращения Δx и Δy находят для каждой стороны хода, округляют до сантиметров и записывают со своим знаком в колонки 8 и 9. Например:

d _42-1

---

= 122,02м;

r = 55^о00^/30^//;

α =124⁰59^/30^//

Для стороны 42-1:

∆x = d× cos r = 122,02 × cos(55^о00^/30^//˚)= 122,02 × 0,573457 = –69,97м

Δy = d × sin r = 122,02м × sin(55^о00^/30^//) = 122,02 × 0,819235 = +99,96м
Уравнивание приращений координат. Линейные невязки теодолитного хода ƒ_х и ƒ_y рассчитываются по формулам:
ƒ_х = Σ _{ΔX практ} - Σ _{ΔX теор};

ƒ_y = Σ _{ΔY практ} - Σ _{ΔY теор.}
где Σ _{ΔX практ} – сумма всех вычисленных Δx;

Σ _{ΔY практ} – сумма вех вычисленных Δy.

В рассматриваемом варианте: Σ _{ΔX практ} = 120,39м

Σ _{ΔY практ} = 319,8 м.
Σ _{ΔX теор} = x_кон – x_нач = x₄₆ – x₄₂ = 251,86 – 131,71 = 120,15м

Σ _{ΔY теор} = y_кон – y_нач = y₄₆ – y₄₂ = 381,84 – 61,93 = 319,91м.

Следовательно:

ƒ_х = + 0,24м

ƒ_y = - 0,04м.
Абсолютная линейная невязка ƒ_абс находится по формуле:
ƒ_абс = ±
ƒ_абс = ± = + 0,25м.
Вычисление относительной невязки хода. Относительная невязка теодолитного хода ƒ_отн определяется как частное от деления абсолютной невязки хода ƒ_абс на длину хода Р, где Р= Σ d.

Например:

Р = 491,97м;
ƒ_отн = = = =

Невязка записывается в виде аликвотной дроби (дробь, в числителе которой единица).

Для теодолитных ходов величина допустимой относительной невязки установлена 1/1000. Сравниваем полученную относительную навязку с допустимой. При этом должно выполняться следующее неравенство;

ƒ_отн ≤ ; т.е. ≤

Для рассматриваемого примера неравенство выполняется, значит, можно распределять линейные невязки по осям координат. В случае, если относительная ошибка превышает установленный допуск, следует тщательно проверять вычисления приращений координат Δx и Δy , их знаки, значения тригонометрических функций румбов, горизонтальных проложений. Если ошибки в вычислениях не обнаружены, то на практике повторяют измерения линий, а обучающийся должен обратиться в таком случае к преподавателю.

---

Линейные невязки ƒ_х и ƒ_y распределяются с обратным знаком прямо пропорционально горизонтальному проложению линии. В каждое приращение координат вычисляют поправку:

υ_ΔX = ; υ_Δy =

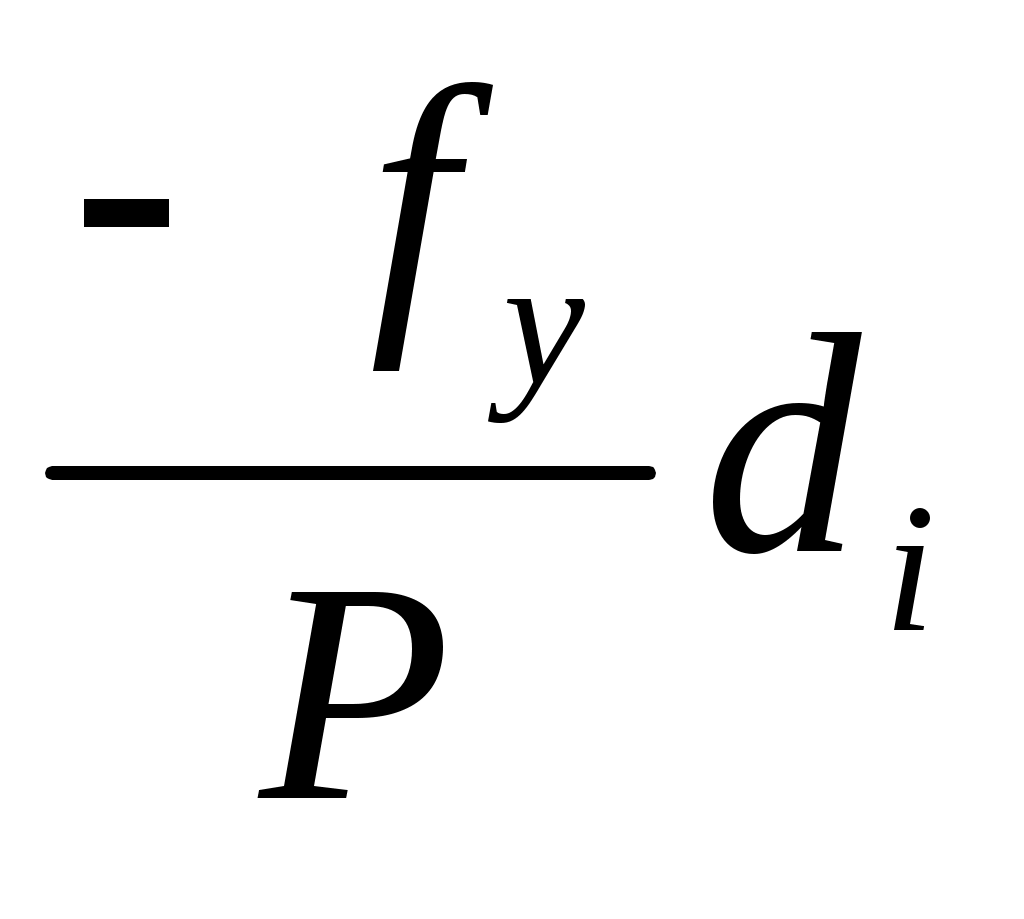
Для удобства вычислений Р и d округляют до целых сотен метров. В рассматриваемом варианте:

Р₁₀₀ = 4,92; d₁₀₀ = 1,22
тогда υ_ΔX = = - 0,06м; υ_Δy = = 0,01м

Контролем вычисления поправок является равенство сумм поправок по соответствующей оси и невязки с обратным знаком

Συ _ΔX = -ƒ_х ; Συ _Δy = - ƒ_y.

Вычисленные поправки записываются в сантиметрах в колонки 10 и 11 ведомости координат красным цветом над соответствующими приращениями.

Исправленные приращения вычисляются по формулам:
Δx_испр = Δx_выч + υ_ΔX = -69,97 + (-0,06) = - 70,03 м

Δy_испр = Δy_выч +υ _Δy = 99,96 + 0,01 = 99,97 м

где Δx_выч и Δy_выч - вычисленные приращения.

Контролем распределения линейных невязок служит равенство суммы исправленных приращений по осям X и Y и теоретических сумм приращения координат:
Σ Δx_испр = ΣΔx_теор или 120,15м = 120,15м,

Σ Δy_испр = ΣΔy_теор или 319,91м =319,91м.

Все вычисления по определению величин невязок, их допустимых значений записываются в колонке 15 ведомости.

Вычисления координат точек теодолитного хода.

Координаты исходных пунктов полигонометрии пп42 и пп46 выписываются красным цветом из табл. 4 в колонку 12 и 13 ведомости.

Координаты точек теодолитного хода вычисляются по формулам:

X_n+1 = X_n + ΔX_испр,

Y_n+1 = Y_n + ΔY_испр,
где X_n+1; Y_n+1 - координаты последующей точки хода соответственно по осям X иY;

X_n; Y_n - координаты предыдущей точки хода соответственно по осям Х и Y.

Вычисления координат производится в следующем порядке:

X₁ = X₄₂ + Δx_42-1 = 131,71+ (-70,03) = 61,68м

X₂ = X₁ + Δx_1-2 = 61,68 + 10,04 = 51,64 м

X₃ = X₂ + Δx_2-3 = 51,64 + 130,21 = 181,85 м

X₄₆ = X₃ + Δx_3-46 = 181,85 + 70,01 = 251,86м

---

Смотрите также файлы

• "Сравнение рабочих характеристик асинхронного двигателя в трехфазном и однофазном режимах".docx

• Стадийность разработки нефтяных месторождений.docx

• 8. Eduardo C. Muoz Journal Electroanalytical Chemistry. 2007. Vol. 611P. 3542.docx

• Контрольная работа Итоговое тестирование за курс 9 класса по информатике в рамках промежуточной аттестации.docx

• Должность) (подпись) (дата) (Фамилия И. О.docx