Задача 2.

В цепи постоянного тока заданы ЭДС 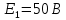и сопротивления резисторов 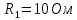, 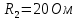. Положения рубильников и остальные данные указаны в таблице 2.

1. 
   Начертить схему своего варианта и показать на ней условные направления токов в ветвях.
   
2. 
   Составить по законам Кирхгофа систему уравнений, необходимых для определения токов (решать систему не требуется).
   
3. 
   Определить токи ветвей методом контурных токов.
   
4. 
   Проверить решение методом узлового напряжения.
   
5. 
   По результатам расчетов нанести на схеме (пунктиром) действительные направления токов.
   

Решение

Дано:

1. 
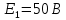
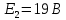
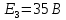
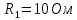
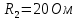
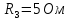
   После замыкания рубильников получаем следующую расчетную схему. Нанесем на нее условные направления токов.
   

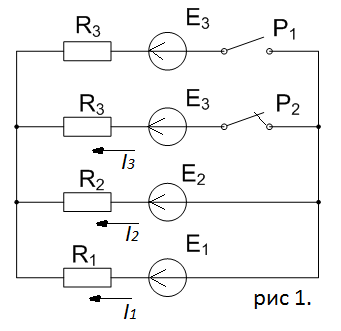
Заменим представленную расчетную схему - упрощенной эквивалентной ей. Нанесем на эквивалентную схему условные обозначения узлов и ветвей.

2. 
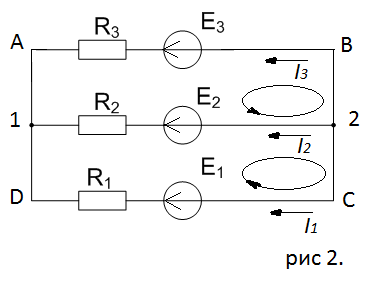
   Составим систему уравнений по законам Кирхгофа.
   

Для расчета электрической цепи постоянного тока по законам Кирхгофа необходимо составить в общем
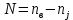– число уравнений (1)
Где 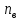– общее число ветвей электрической цепи, 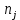- число ветвей содержащих источники тока
По первому закону Кирхгофа максимальное число независимых уравнений равно:
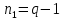(2)
Где

---

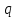
- число узлов электрической цепи

По второму закону Кирхгофа максимальное число независимых уравнений равно:
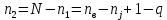(3)
Из рис 2. Определяем:

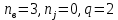
Таким образом, общее число уравнений по законам Кирхгофа равно:


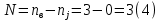
Число уравнений по первому закону Кирхгофа определяем из (2):

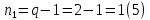
Число уравнений по второму закону Кирхгофа определяем из (3):

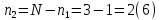
Таким образом, по первому закону Кирхгофа максимальное число независимых уравнений равно 1, по второму закону Кирхгофа максимальное число независимых уравнений равно 2.
По первому закону Кирхгофа составим уравнение для узла 2 (рис 2.)

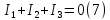
По второму закону Кирхгофа составим уравнения для контуров (A-B-2-1) и (C-D-1-2). Условные направления положительного обхода контуров показаны на (рис 2.).


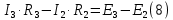
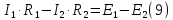
Уравнения (7),(8),(9) следует объединить в систему:

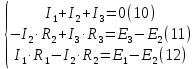
Подставляя, в полученную систему числовые значения получим:

3. 
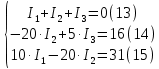
   Определим токи ветвей методом контурных токов. Введем контурные токи и покажем направления положительного обхода контуров (рис 3.).
   

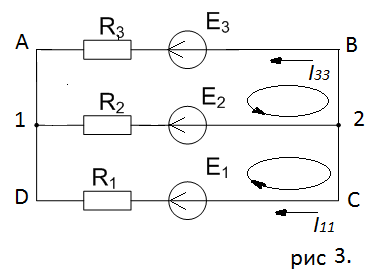
Для контуров (C-D-1-2), (A-B-2-1) составляем уравнения по второму закону Кирхгофа.

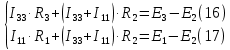
Подставляя, в систему числовые значения получим:

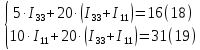
Решая, эту систему получим:


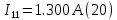
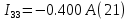
Теперь определим токи ветвей :
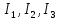Из рис 2. и рис 3. видно что:

---

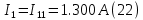
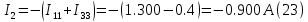
Знак минус указывает на то, что истинное направление тока 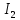противоположно показанному на рис 2.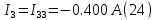

4. 
   Проверим решение методом узлового напряжения.
   

Принимаем потенциал узла (1) равным нулю т.е. 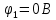, а для узла (2) составляем уравнение по первому закону Кирхгофа (рис 2.).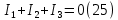

Выразим токи ветвей через потенциалы узлов:



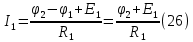
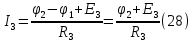
Уравнения (25),(26),(27),(28) следует объединить в систему:

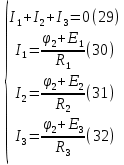
Складывая (30),(31),(32) и учитывая (29) получим:

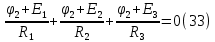
Перепишем уравнение (33) в следующем виде:

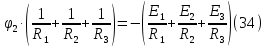
Далее преобразуем уравнение (34) учитывая что:

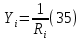
Где 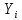– проводимость 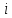– ой ветви в результате получим. В результате уравнение (34) преобразуется к виду: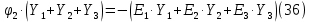

Выражая из (36) 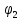получим: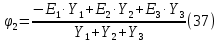

Найдем числовые значения проводимостей ветвей:



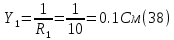
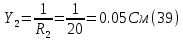
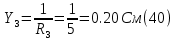
Подставляя числовые значения в (37) находим потенциал :

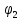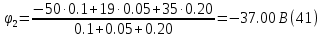
Далее из (30) следует:

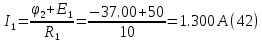
Из (31) следует:

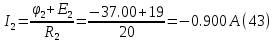
Из (32) следует:

---

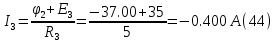
Результаты расчетов токов ветвей по методам контурных токов и узлового напряжения совпадают.
Задача 4. В трехфазную цепь с линейным напряжением 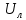включена трехфазная симметричная нагрузка в звезду или треугольник. В каждой фазе нагрузки последовательно соединены резистор 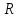и катушка 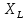(или конденсатор ).

1. 
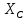   Начертить электрическую схему и нанести условные положительные направления напряжений и токов.
   
2. 
   Определить линейные и фазные токи, коэффициент мощности, активную, реактивную и полную мощности.
   
3. 
   Построить в масштабе векторную диаграмму напряжений и токов.
   

Решение

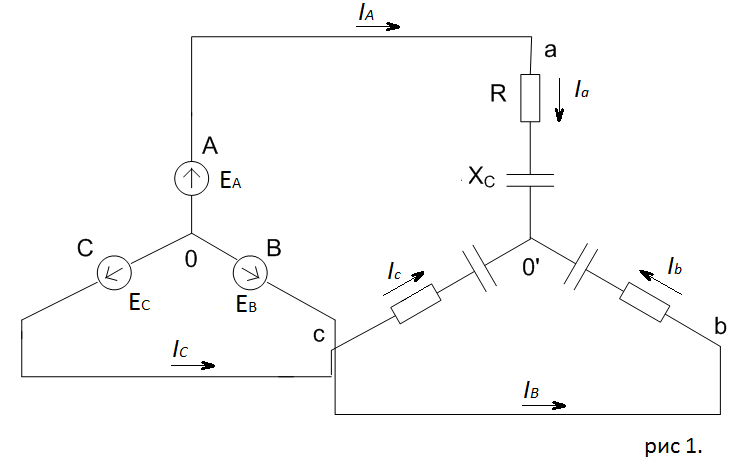
Дано:

1. 
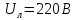
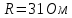
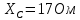
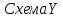
   Чертим схему трехфазной цепи и наносим условные положительные направления напряжений и токов.
   

2. 
   Определим линейные и фазные токи, коэффициент мощности, активную, реактивную и полную мощности.
   

Определяем модуль действующих значений фазных ЭДС. В данном случае нагрузка соединена звездой поэтому имеем:

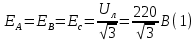
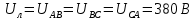– действующее напряжение между линейными проводами.
Определяем комплексы действующих фазных ЭДС:



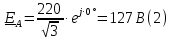
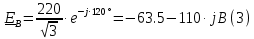
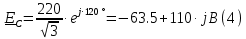
Определяем комплексы фаз нагрузки:

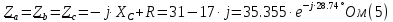
Преобразуем исходную цепь.



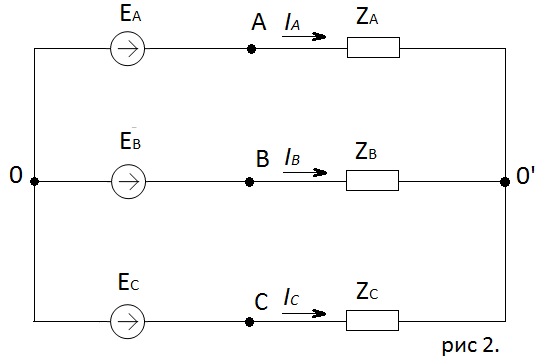
Для полученной схемы имеем:

---

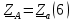
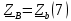
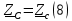
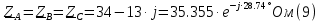
Для цепи с симметричной нагрузкой напряжение смещения нуля нагрузки


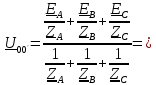
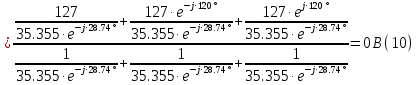
Действующие линейные токи и токи фаз нагрузки равны:





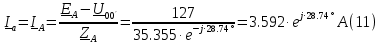
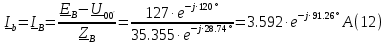
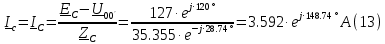
Находим мощность трехфазной системы. Комплекс полной мощности системы равен:




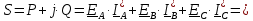
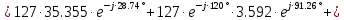
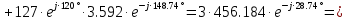
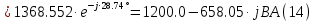
Активная мощность системы равна:

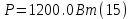
Реактивная мощность системы равна:

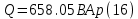
Полная мощность системы равна:

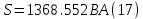
Коэффициент мощности системы:

3. 
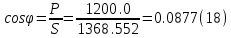
   Строим в масштабе векторную диаграмму напряжений и токов.
   

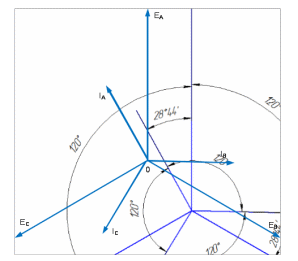
Задача 5.

Трехфазный силовой трансформатор имеет следующие паспортные данные: номинальная мощность 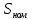, номинальные линейные напряжения первичной и вторичной обмоток 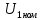, и 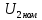, мощность потерь короткого замыкания 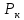, напряжение короткого замыкания 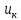. Известна также схема соединения обмоток.

1. 
   Начертить электрическую схему трансформатора.
   
2. 
   Определить номинальные линейные токи, токи в обмотках и фазные напряжения; активные сопротивления обмоток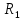 и 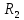; КПД при заданном коэффициенте мощности и коэффициентах нагрузки .
   
3. 
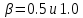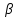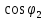   Определить при тех же значениях и вторичное напряжение 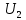и построить внешнюю характеристику .
   

---

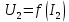Смотрите также файлы

• Таратылан параметрлі тізбектер тоэ2 дріс.pptx

• 1 Анализ способов обработки глубоких отверстий, конструкций инструментов для глубокого сверления, сил, действующих на сверло, факторов, оказывающих влияние на силы, моделей контакта при трении.docx

• Курсовая по психологии по подготовки 44. 03. 01 образование, профилю Начальное поб17036064.docx

• Лабораторная работа 8 Получение изопропилового спирта сернокислотной гидратацией пропилена.docx

• 5 Ценностносмысловая позиция учителя.docx