Файл: Курсовой проект по дисциплине Математическое моделирование процессов чрезвычайных ситуаций Тема проекта.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 80
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
загрязненной жидкости извлекают ценные вещества, попавшие в воду в процессе производства.
2 Физическая постановка задачи
Рассмотрим нестационарную двумерную задачу переноса загрязняющей примеси от заданного источника в русле реки. В рассматриваемой области в начальный момент времени t=0 задано распределение концентрации загрязняющей примеси Сe=0. Считается, что скорость течения реки на прямолинейном участке постоянная в заданной области. Задан постоянно действующий источник выброса загрязнения внутри расчетной области. Необходимо найти распределение концентрации в заданной области течения реки в различные моменты времени для различных значений параметров (Рисунок 1).
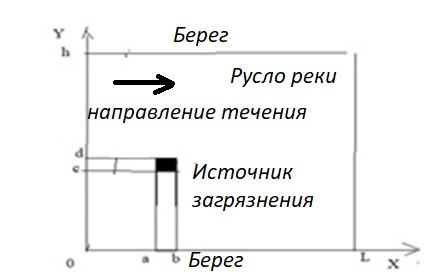
Рисунок 1 – Схема расчетной области
3 Математическая постановка задачи
В связи с тем, что протяженность реки в горизонтальном направлении значительно превышает вертикальные размеры, математически процесс переноса загрязняющего вещества с течением времени в данной области описывается с помощью следующей системы дифференциальных уравнений (уравнений неразрывности, движения и диффузии) в горизонтальной плоскости с соответствующими начальными и граничными условиями:
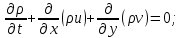 (1)
(1)
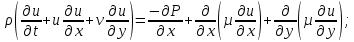 (2)
(2)
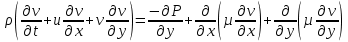 ; (3)
; (3)
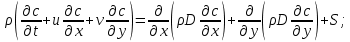 (4)
(4)
Начальные и граничные условия имеют следующий вид:
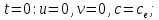 (5)
(5)
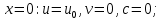 (6)
(6)
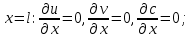 (7)
(7)
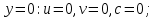 (8)
(8)
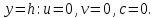 (9)
(9)
Где t – время, u, v – проекции вектора скорости на оси x, y, Р – давление, С – концентрациязагрязняющей примеси; ρ – плотность, µ, D – коэффициенты вязкости и диффузии для воды; h – ширина реки, L – длина участка реки. Источник S задан по формуле:
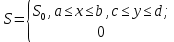
S0= (3, 6, 8) кг/(м3 с), a=6 м, b=7 м, c=2 м, d=2.5 м, u0=0.2 м/c, l=40 м, h=10 м
4 Численный метод решения
Расчётную область разбиваем на некоторое число контрольных объёмов. Затем исходную систему уравнений интегрируем по каждому контрольному объёму. В результате получается алгебраическая система нелинейных уравнений.
Для численного интегрирования исходной системы уравнений используется метод контрольного объёма (Рисунок 2)
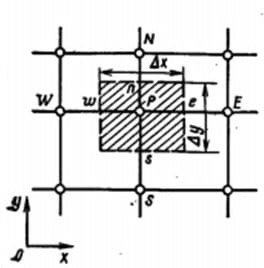
Рисунок 2 – Контрольный объём
Вид двухмерного дискретного аналога можно записать как:
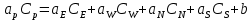
где
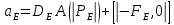
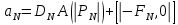
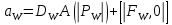
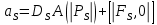
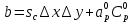
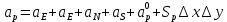
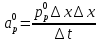
Здесь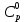 и
и 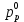 обозначают известные значения для времени t, а все другие величины (CР, CЕ, CW, CN, CS) представляют собой неизвестные величины для времени t+Δt. Соответствующие проводимости представим в виде:
обозначают известные значения для времени t, а все другие величины (CР, CЕ, CW, CN, CS) представляют собой неизвестные величины для времени t+Δt. Соответствующие проводимости представим в виде:
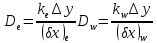
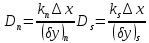
а числа Пекле:
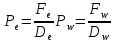
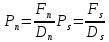
Коэффициенты в соседних точках аE, аW, аN и аS учитывают влияние конвекции и диффузии для четырех граней контрольного объема, которые зависят проводимости D. Член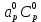 характеризует известную величину для контрольного объема (для времени t), отнесенную к шагу по времени.
характеризует известную величину для контрольного объема (для времени t), отнесенную к шагу по времени.
Проход по горизонтальным линиям:
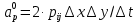
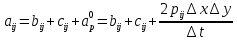
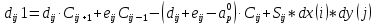
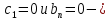 на границе области
на границе области
Осуществляем расчёт по горизонтальной линии, применяя метод TDMA:
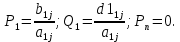
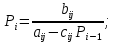
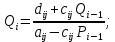
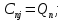
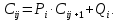
Проход по вертикальным линиям:
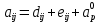
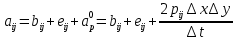
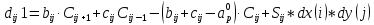
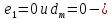 на границе области
на границе области
Вычислим коэффициенты:
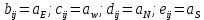
Далее осуществляем расчёт по вертикальной линии, применяя метод TDMA:
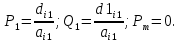
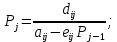
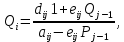
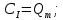
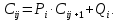
5 Результаты и их анализ
На рис.3 представлено распределение концентрации в момент времени 1 с и источником загрязнения равным 3 кг/(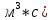
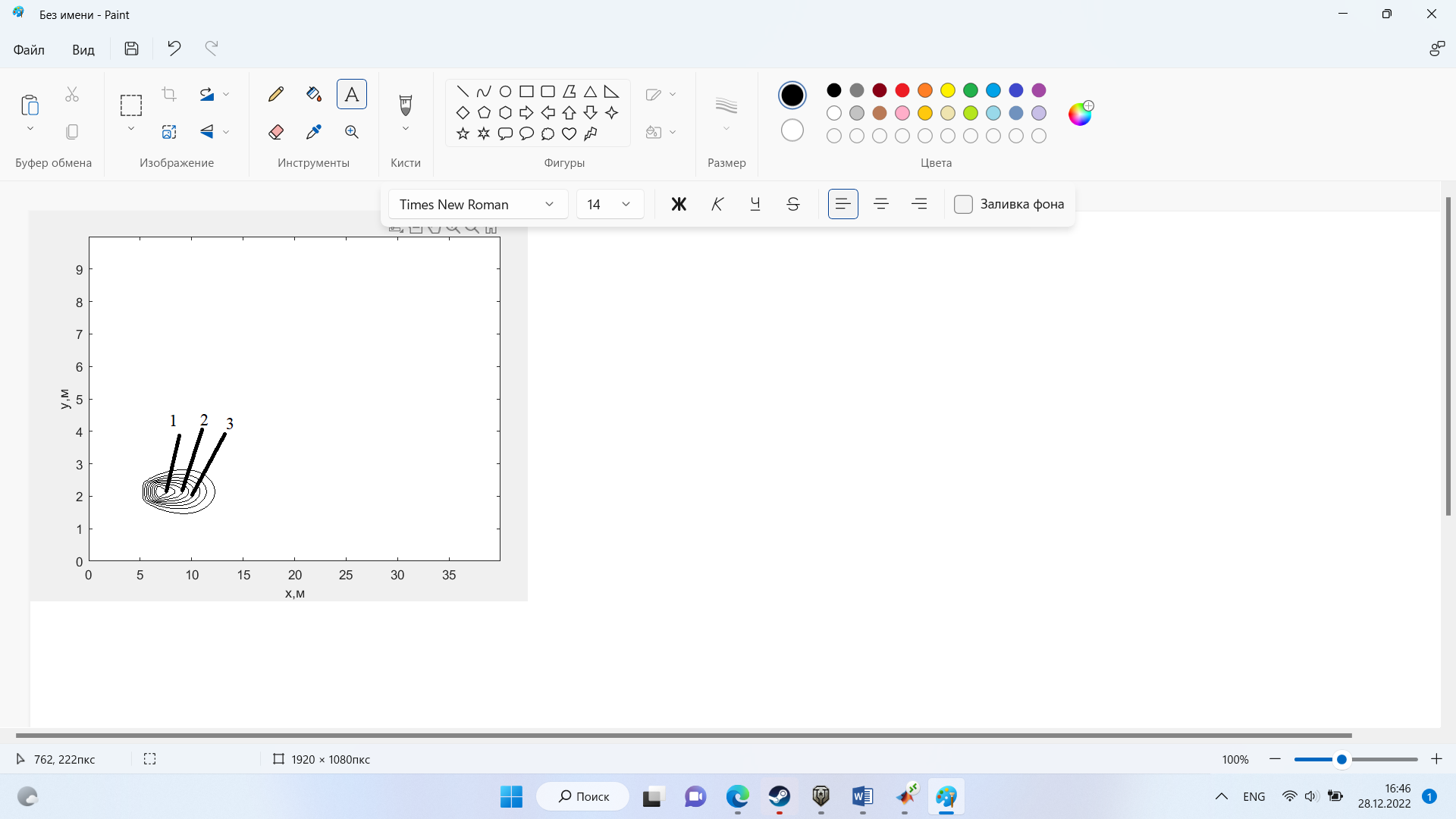
Рисунок 3 – график в момент времени 1с.
На рис.4 представлено распределение концентрации в момент времени 5 с и источником загрязнения равным 3 кг/(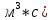
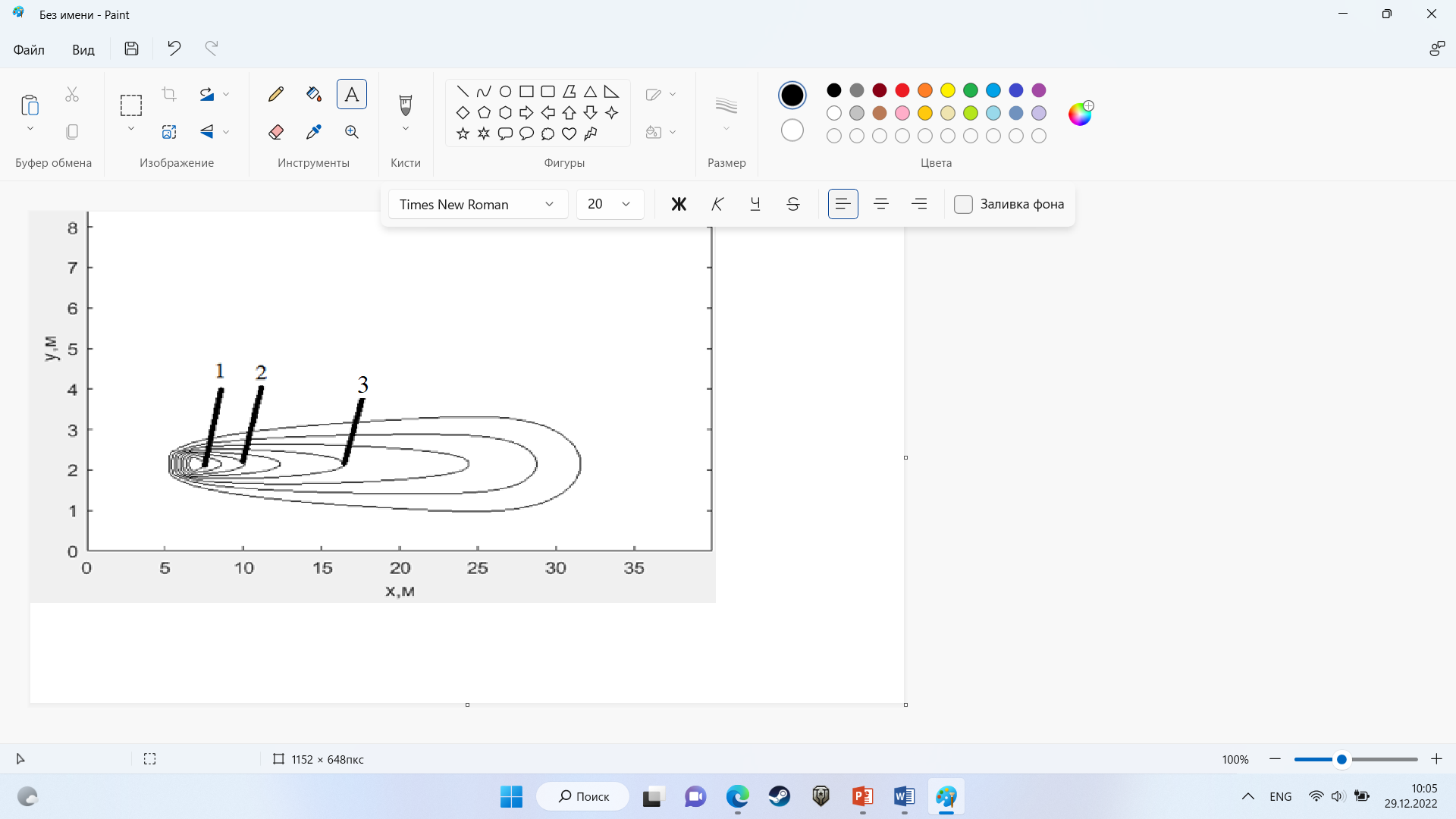
Рисунок 4 – график в момент времени 5с.
На рис.5 представлено распределение концентрации в момент времени 10 с и источником загрязнения равным 3 кг/(
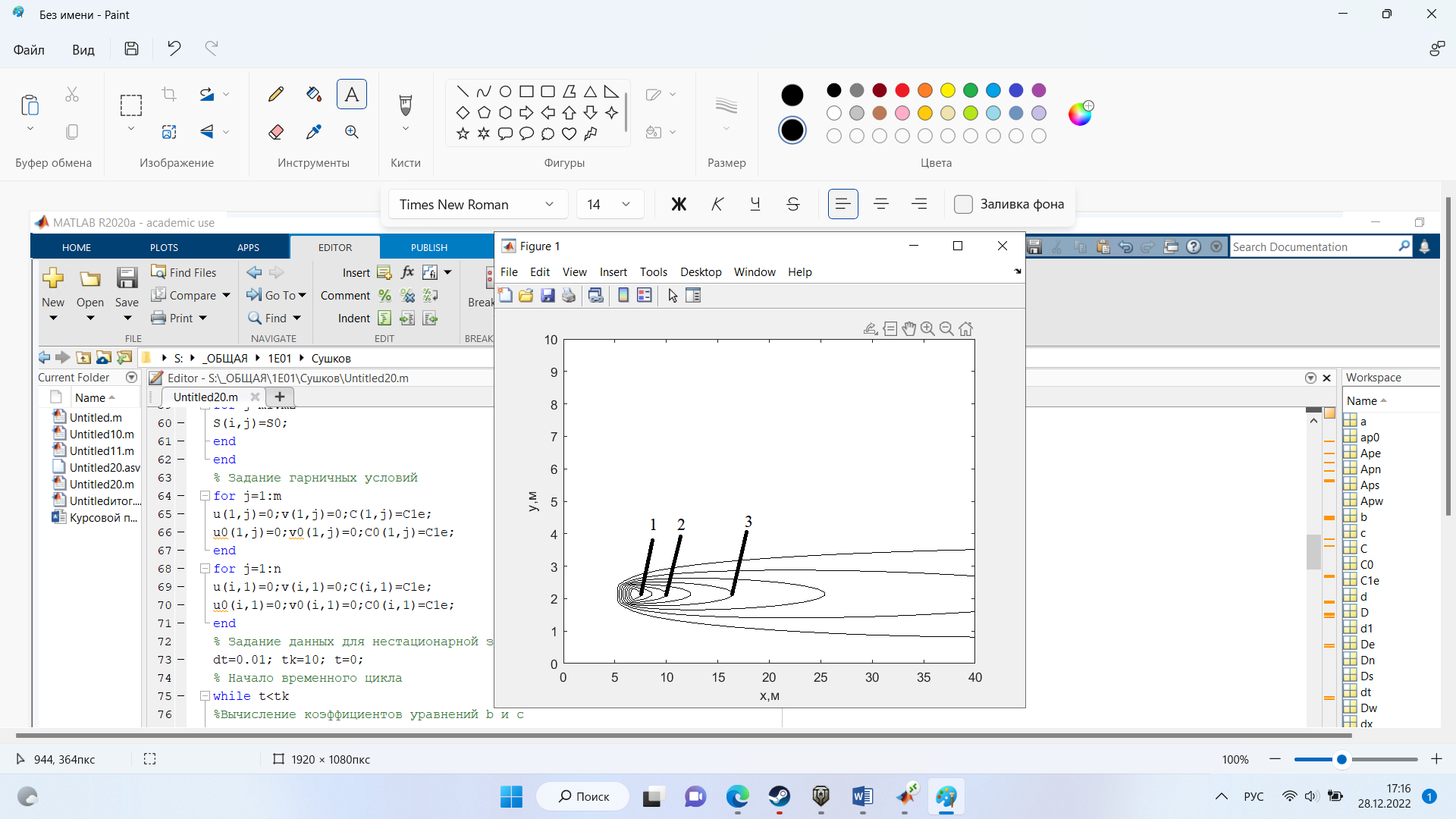
Рисунок 5 – график в момент времени 10с.
На рис.6 представлено распределение концентрации в момент времени 10 с и источником загрязнения равным 6 кг/(
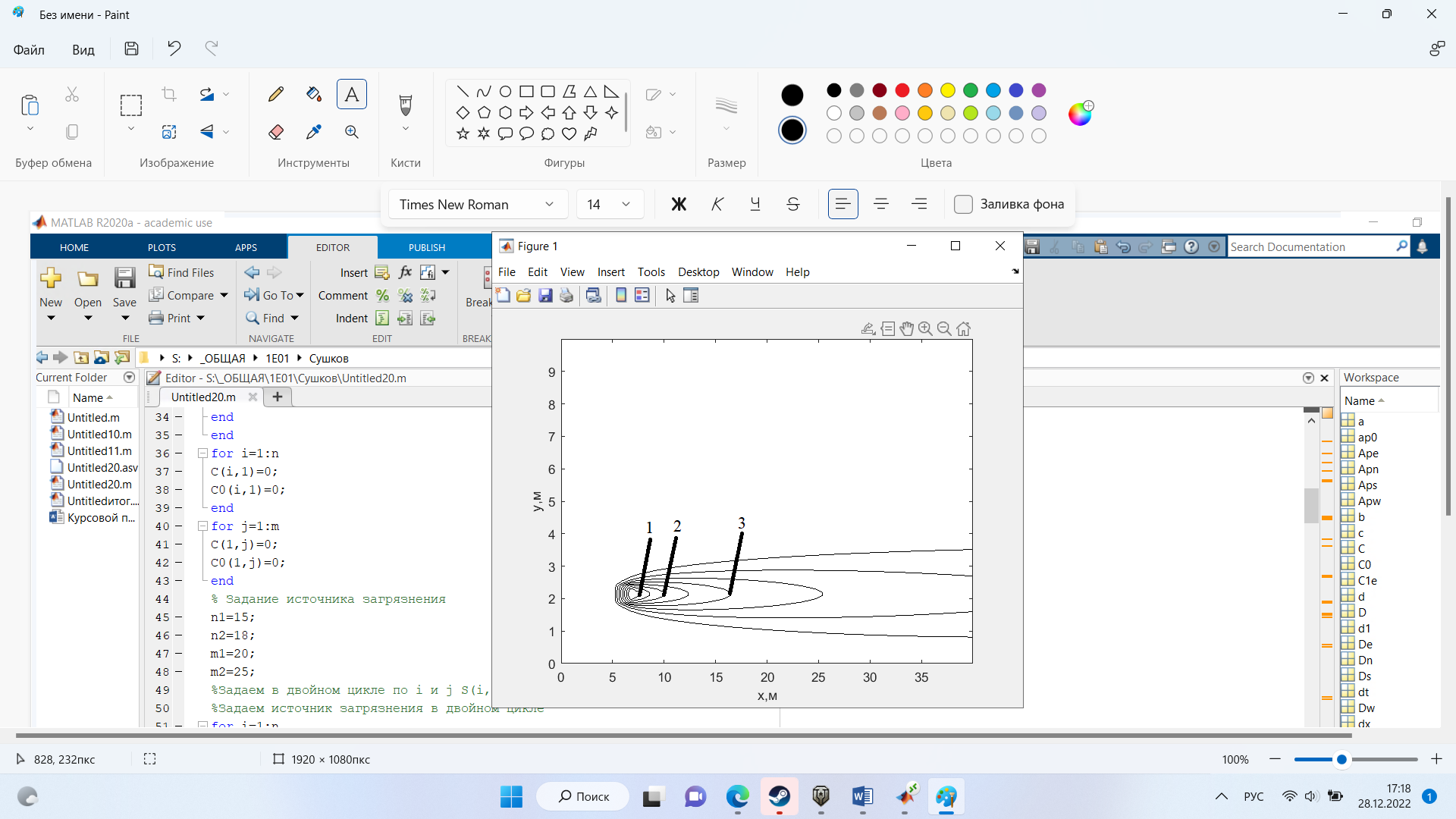
Рисунок 6 – график в момент времени 10с.
На рис.7 представлено распределение концентрации в момент времени 5 с и источником загрязнения равным 6 кг/(
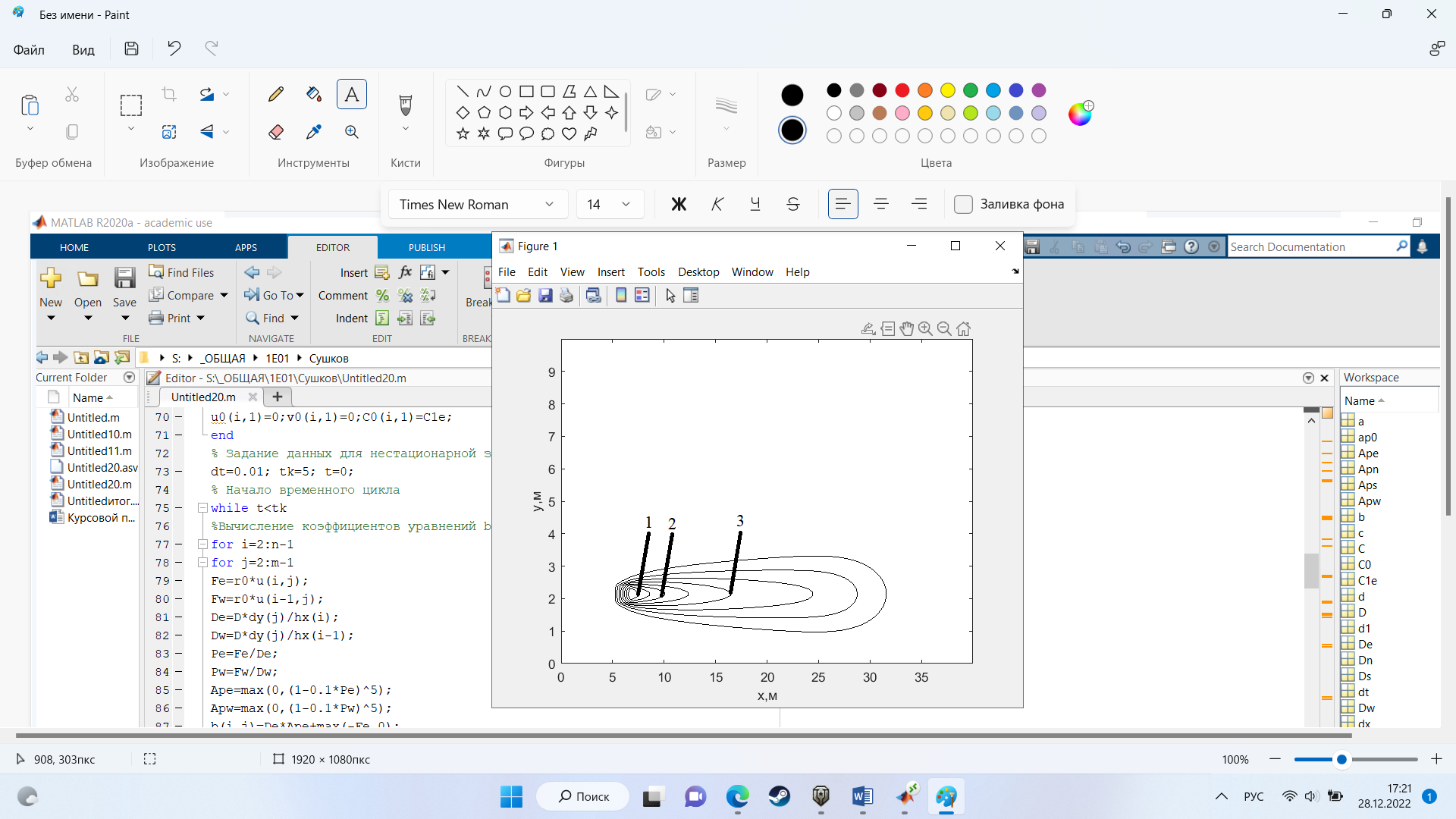
Рисунок 7 – график в момент времени 5с.
На рис.8 представлено распределение концентрации в момент времени 1 с и источником загрязнения равным 6 кг/(
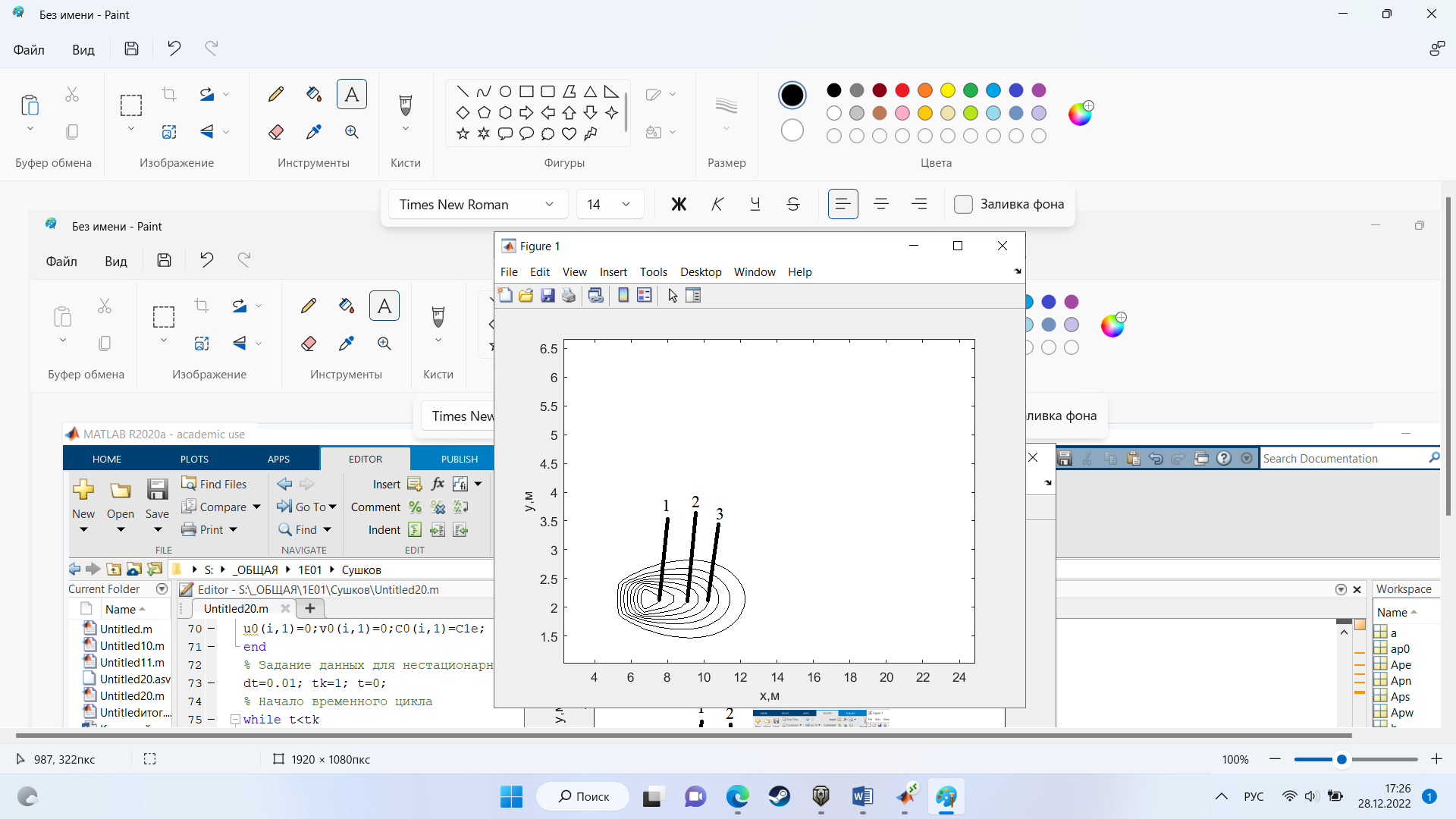
Рисунок 8 – график в момент времени 1с.
На рис.9 представлено распределение концентрации в момент времени 1 с и источником загрязнения равным 9 кг/(
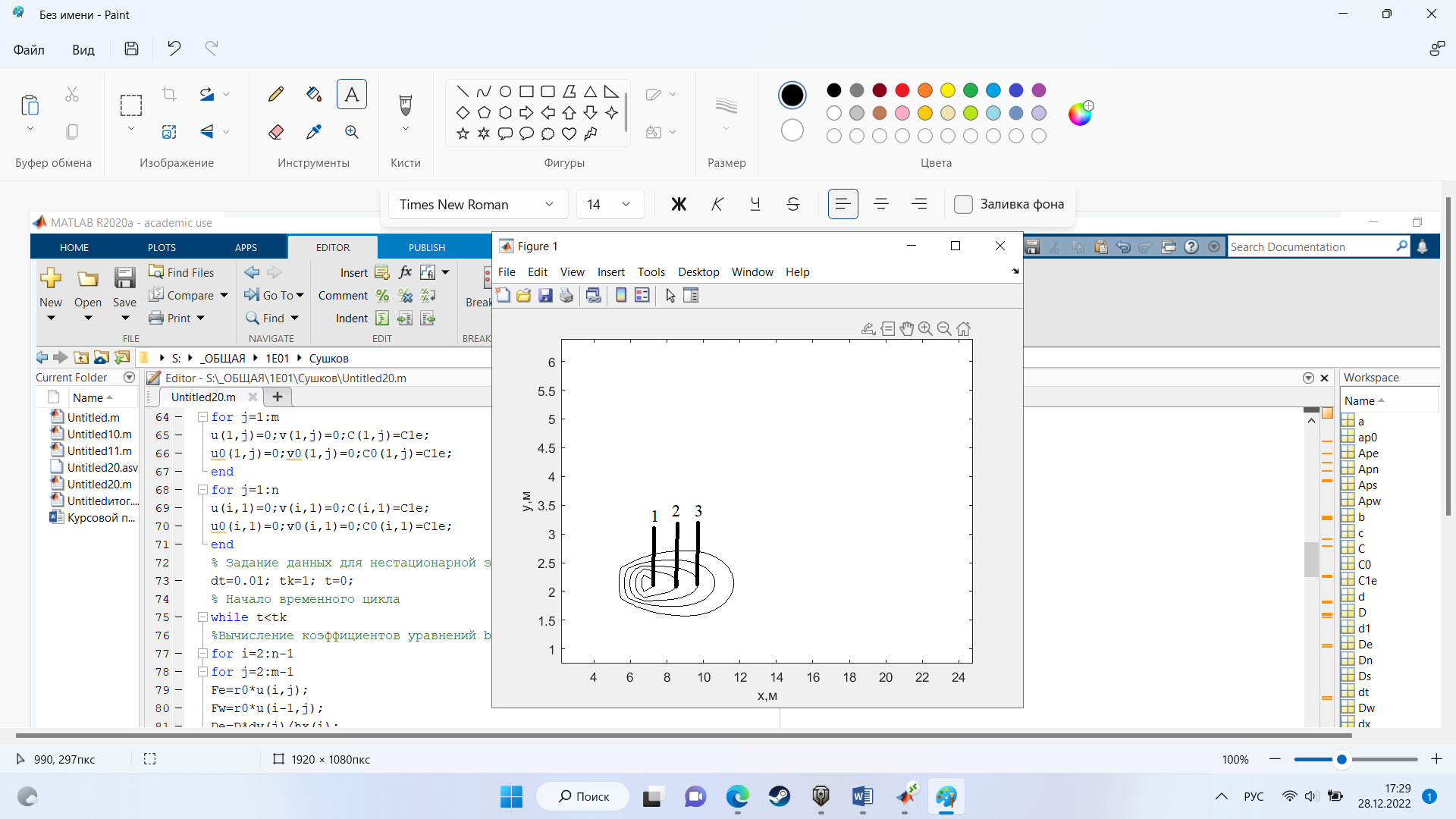
Рисунок 9 – график в момент времени 1с.
На рис.10 представлено распределение концентрации в момент времени 5 с и источником загрязнения равным 9 кг/(
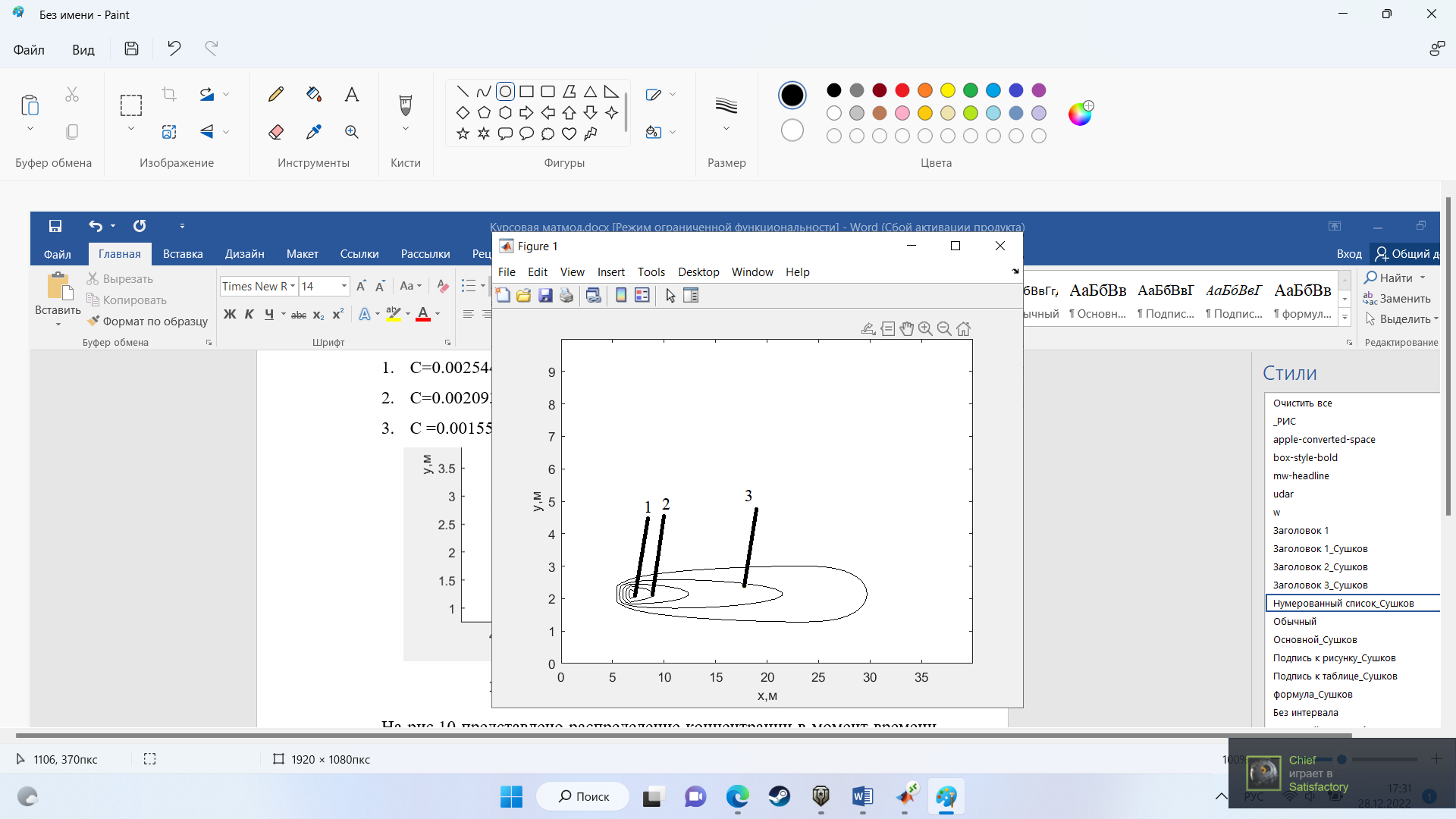
Рисунок 10 – график в момент времени 5с.
На рис.11 представлено распределение концентрации в момент времени 10 с и источником загрязнения равным 9 кг/(
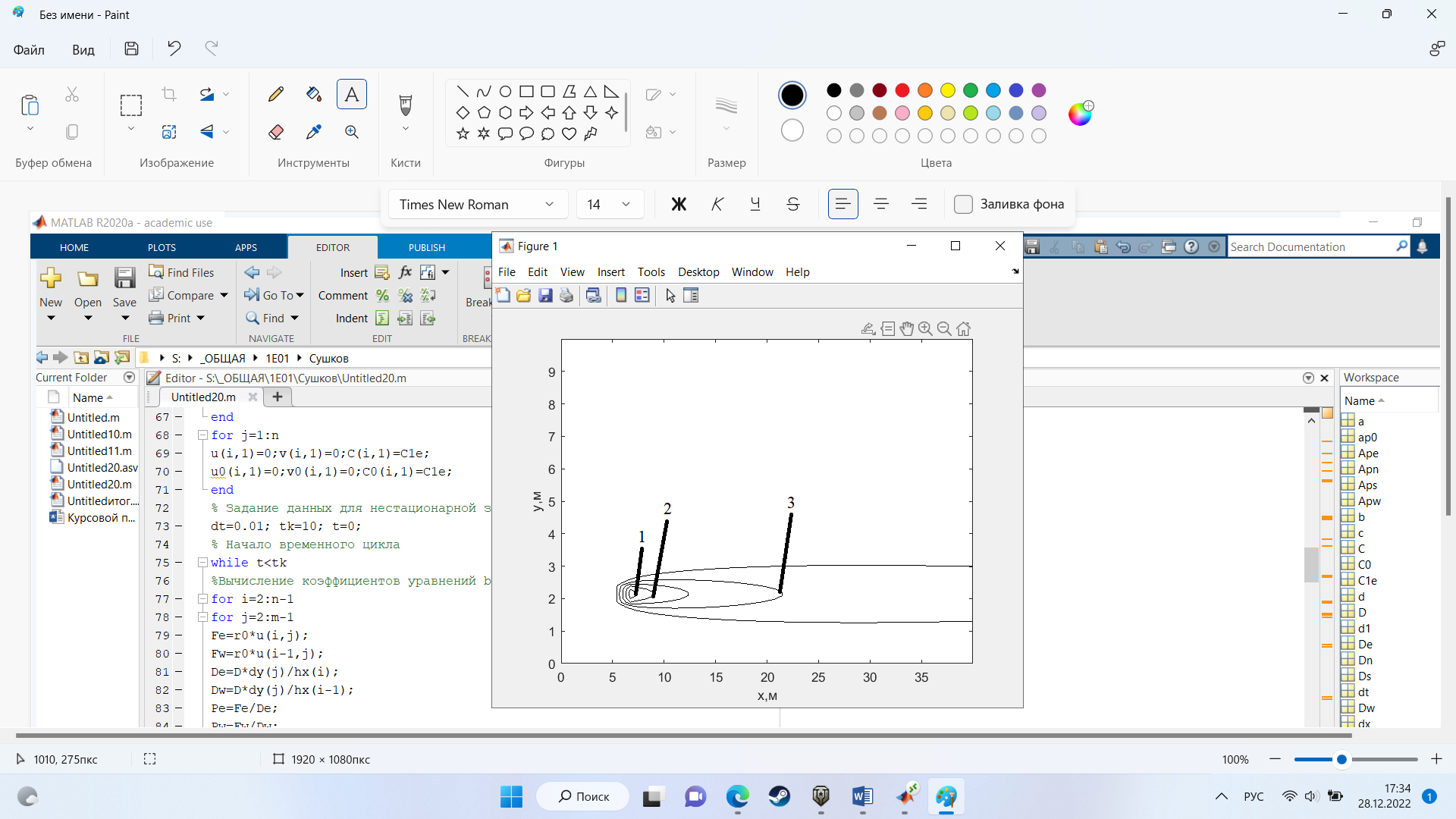
Рисунок 11 – график в момент времени 10с.
6 Выводы
В результате проделанной работы можно сделать несколько вывод зависимости распределения загрязнения в водной среде от изменения параметров среды для данной задачи:
7 Литература
8 Приложение
% Задание исходных данных
L=40;h=10;u0=0.5;r0=1000.2;S0=9;D=80;C1e=0;n=100;m=100;
% Задание размеров шагов по направлениям
dx(1)=0; dx(n)=0;
% Задание размеров шагов по направлениям x y:
for i=2:n-1
dx(i)=L/(n-2);
end
for i=1:n-1
hx(i)=(dx(i)+dx(i+1))/2;
end
dy(1)=0 ;dy(m)=0;
for j=2:m-1
dy(j)=h/(m-2);
end
for j=1:m-1
hy(j)=(dy(j)+dy(j+1))/2;
end
%Задание размеров шагов по направлениям
x(1)=0;
for i=1:n-1
x(i+1)=hx(i)+x(i);
end
% В цикле по j
y(1)=0;
for j=1:m-1
y(j+1)=hy(j)+y(j);
end
% Задание начальных условий
for i=2:n
for j=2:m
C0(i,j)=0;
C(i,j)=0;
end
end
for i=1:n
C(i,1)=0;
C0(i,1)=0;
end
for j=1:m
C(1,j)=0;
C0(1,j)=0;
end
% Задание источника загрязнения
n1=15;
n2=18;
m1=20;
m2=25;
%Задаем в двойном цикле по i и j S(i,j)=0
%Задаем источник загрязнения в двойном цикле
for i=1:n
for j=1:m
S(i,j)=0;
u(i,j)=0.5;
v(i,j)=0;
end
end
for i=n1:n2
for j=m1:m2
2 Физическая постановка задачи
Рассмотрим нестационарную двумерную задачу переноса загрязняющей примеси от заданного источника в русле реки. В рассматриваемой области в начальный момент времени t=0 задано распределение концентрации загрязняющей примеси Сe=0. Считается, что скорость течения реки на прямолинейном участке постоянная в заданной области. Задан постоянно действующий источник выброса загрязнения внутри расчетной области. Необходимо найти распределение концентрации в заданной области течения реки в различные моменты времени для различных значений параметров (Рисунок 1).

Рисунок 1 – Схема расчетной области
3 Математическая постановка задачи
В связи с тем, что протяженность реки в горизонтальном направлении значительно превышает вертикальные размеры, математически процесс переноса загрязняющего вещества с течением времени в данной области описывается с помощью следующей системы дифференциальных уравнений (уравнений неразрывности, движения и диффузии) в горизонтальной плоскости с соответствующими начальными и граничными условиями:
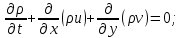 (1)
(1)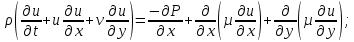 (2)
(2)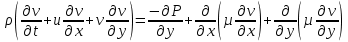 ; (3)
; (3)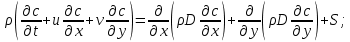 (4)
(4)Начальные и граничные условия имеют следующий вид:
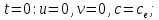 (5)
(5)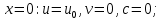 (6)
(6)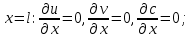 (7)
(7)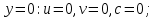 (8)
(8)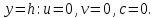 (9)
(9)Где t – время, u, v – проекции вектора скорости на оси x, y, Р – давление, С – концентрациязагрязняющей примеси; ρ – плотность, µ, D – коэффициенты вязкости и диффузии для воды; h – ширина реки, L – длина участка реки. Источник S задан по формуле:
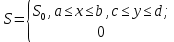
S0= (3, 6, 8) кг/(м3 с), a=6 м, b=7 м, c=2 м, d=2.5 м, u0=0.2 м/c, l=40 м, h=10 м
4 Численный метод решения
Расчётную область разбиваем на некоторое число контрольных объёмов. Затем исходную систему уравнений интегрируем по каждому контрольному объёму. В результате получается алгебраическая система нелинейных уравнений.
Для численного интегрирования исходной системы уравнений используется метод контрольного объёма (Рисунок 2)

Рисунок 2 – Контрольный объём
Вид двухмерного дискретного аналога можно записать как:
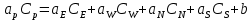
где
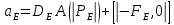
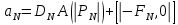
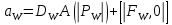
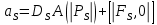
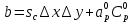
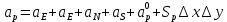
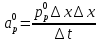
Здесь
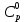 и
и 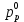 обозначают известные значения для времени t, а все другие величины (CР, CЕ, CW, CN, CS) представляют собой неизвестные величины для времени t+Δt. Соответствующие проводимости представим в виде:
обозначают известные значения для времени t, а все другие величины (CР, CЕ, CW, CN, CS) представляют собой неизвестные величины для времени t+Δt. Соответствующие проводимости представим в виде: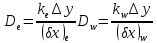
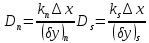
а числа Пекле:
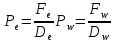
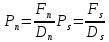
Коэффициенты в соседних точках аE, аW, аN и аS учитывают влияние конвекции и диффузии для четырех граней контрольного объема, которые зависят проводимости D. Член
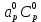 характеризует известную величину для контрольного объема (для времени t), отнесенную к шагу по времени.
характеризует известную величину для контрольного объема (для времени t), отнесенную к шагу по времени.Проход по горизонтальным линиям:
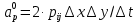
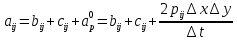
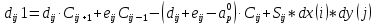
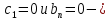 на границе области
на границе областиОсуществляем расчёт по горизонтальной линии, применяя метод TDMA:
-
Вычисленные коэффициенты уравнений используем для вычисления P1 и Q1
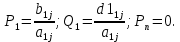
-
Используем рекуррентные соотношения
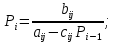
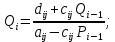
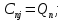
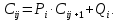
Проход по вертикальным линиям:
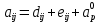
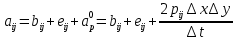
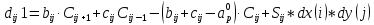
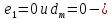 на границе области
на границе областиВычислим коэффициенты:
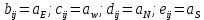
Далее осуществляем расчёт по вертикальной линии, применяя метод TDMA:
-
Вычисленные коэффициенты уравнений используем для вычисления P1 и Q1
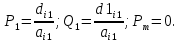
-
Используем рекуррентные соотношения
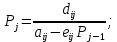
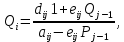
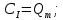
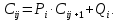
5 Результаты и их анализ
На рис.3 представлено распределение концентрации в момент времени 1 с и источником загрязнения равным 3 кг/(
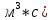
-
С=0.0007979
-
С=0.0005839 -
С =0.0004113

Рисунок 3 – график в момент времени 1с.
На рис.4 представлено распределение концентрации в момент времени 5 с и источником загрязнения равным 3 кг/(
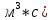
-
С=0.000802
-
С=0.0006011 -
С =0.0003986

Рисунок 4 – график в момент времени 5с.
На рис.5 представлено распределение концентрации в момент времени 10 с и источником загрязнения равным 3 кг/(

-
С=0.000802
-
С=0.0006257 -
С =0.0003986

Рисунок 5 – график в момент времени 10с.
На рис.6 представлено распределение концентрации в момент времени 10 с и источником загрязнения равным 6 кг/(

-
С=0.001604
-
С=0.001125 -
С =0.0007745

Рисунок 6 – график в момент времени 10с.
На рис.7 представлено распределение концентрации в момент времени 5 с и источником загрязнения равным 6 кг/(

-
С=0.001604
-
С=0.001202 -
С =0.0007877

Рисунок 7 – график в момент времени 5с.
На рис.8 представлено распределение концентрации в момент времени 1 с и источником загрязнения равным 6 кг/(

-
С=0.001596
-
С=0.001168 -
С =0.0008293

Рисунок 8 – график в момент времени 1с.
На рис.9 представлено распределение концентрации в момент времени 1 с и источником загрязнения равным 9 кг/(

-
С=0.002544
-
С=0.002093 -
С =0.001553

Рисунок 9 – график в момент времени 1с.
На рис.10 представлено распределение концентрации в момент времени 5 с и источником загрязнения равным 9 кг/(

-
С=0.002321
-
С=0.00196 -
С =0.001001

Рисунок 10 – график в момент времени 5с.
На рис.11 представлено распределение концентрации в момент времени 10 с и источником загрязнения равным 9 кг/(

-
С=0.002321
-
С=0.002053 -
С =0.0009938

Рисунок 11 – график в момент времени 10с.
6 Выводы
В результате проделанной работы можно сделать несколько вывод зависимости распределения загрязнения в водной среде от изменения параметров среды для данной задачи:
-
С увеличением времени, распределение загрязнения в водной среде изменяется – увеличивается область концентраций; -
С увлечением мощности источника загрязнения, область концентраций также увеличивается.
-
В пределах источника концентрация самая большая, а дальше идет на уменьшение
7 Литература
-
Кичигин В.И. Водоотводящие системы промышленных предприятий: Учебное пособие. – М.: Издательство АСВ, 2011. – 656 с. -
Селина А.А. Проблемы очистки сточных вод / Селина А.А. // Промышленные страницы Сибири. – 2018. - № 130. – С. 30-32. -
Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. – М.: Энергоатомиздат, 1984. – 152 с. -
Дьяконов В.П. MATLAB. Полный самоучитель. – М.: ДМК Пресс, 2012.
-
Загрязнение воды: пути решения экологической проблемы [Электронный ресурс]. – режим доступа: https://bezotxodov.ru
8 Приложение
% Задание исходных данных
L=40;h=10;u0=0.5;r0=1000.2;S0=9;D=80;C1e=0;n=100;m=100;
% Задание размеров шагов по направлениям
dx(1)=0; dx(n)=0;
% Задание размеров шагов по направлениям x y:
for i=2:n-1
dx(i)=L/(n-2);
end
for i=1:n-1
hx(i)=(dx(i)+dx(i+1))/2;
end
dy(1)=0 ;dy(m)=0;
for j=2:m-1
dy(j)=h/(m-2);
end
for j=1:m-1
hy(j)=(dy(j)+dy(j+1))/2;
end
%Задание размеров шагов по направлениям
x(1)=0;
for i=1:n-1
x(i+1)=hx(i)+x(i);
end
% В цикле по j
y(1)=0;
for j=1:m-1
y(j+1)=hy(j)+y(j);
end
% Задание начальных условий
for i=2:n
for j=2:m
C0(i,j)=0;
C(i,j)=0;
end
end
for i=1:n
C(i,1)=0;
C0(i,1)=0;
end
for j=1:m
C(1,j)=0;
C0(1,j)=0;
end
% Задание источника загрязнения
n1=15;
n2=18;
m1=20;
m2=25;
%Задаем в двойном цикле по i и j S(i,j)=0
%Задаем источник загрязнения в двойном цикле
for i=1:n
for j=1:m
S(i,j)=0;
u(i,j)=0.5;
v(i,j)=0;
end
end
for i=n1:n2
for j=m1:m2