ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 23
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Урок алгебры в 10 классе
Тема: «Логарифмическая функция, её свойства и график»
Цели:
-
Образовательная: Ввести понятие логарифмической функции с применением прошлого опыта, дать определение. Изучить основные свойства логарифмической функции. Сформировать умение выполнять построение графика логарифмической функции. -
Развивающая: Выработать умение выделять главное, сравнивать, обобщать. Формировать графическую культуру учащихся. -
Воспитательная: Показать взаимосвязь математики с окружающей действительностью. Формировать навыки общения, диалога, умение работать в коллективе.
Тип урока: Комбинированный
Методы обучения: Частично-поисковый, диалоговый.
Ход урока.
1.Актуализация прошлого опыта:
Учащимся предлагаются устные упражнения с использованием определения логарифма, его свойств, формул перехода к новому основанию, решения простейших логарифмических и показательных уравнений, примеров на нахождение области допустимых значений под логарифмических выражений
Устные упражнения Устная работа.
1) Вычислить, пользуясь определением логарифма: log28; log416;
; 
; 
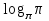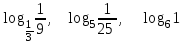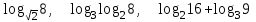.2) Вычислить, используя основное логарифмическое тождество:
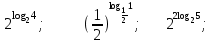
.3) Решите уравнение, используя определение:
4) Выясните, при каких значениях x имеет смысл выражение:
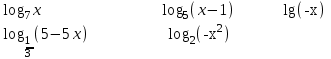
5) Найдите значение выражения, используя свойства логарифмов:
2. Изучение темы. Учащимся предлагается решить показательные уравнения: 2х=у; (
)х =у. с помощью выражения переменной х через переменную у. В результате этой работы получаются формулы, которые задают функции, незнакомые учащимся. 
,
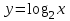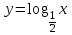.Вопрос : «Как бы вы назвали эту функции?» учащиеся говорят, что она логарифмическая, так как переменная стоит под знаком логарифма: 
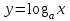. Вопрос. Дайте определение функции. Определение: Функцию, заданную формулой у=logax называют логарифмической с основанием а (а>0, а
1)III. Исследование функции y=logax
Совсем недавно мы ввели понятие логарифма положительного числа по положительному и отличному от 1 основанию а. Для любого положительного числа можно найти логарифм по заданному основанию. Но тогда следует подумать и о функции вида у=logax,
и о ее графике и свойствах. Функцию, заданную формулой у=logax называют логарифмической с основанием а (а>0, а 1)Основные свойства логарифмической функции:
1. Областью определения логарифмической функции будет являться все множество положительных действительных чисел. Для краткости его еще обозначают R+. Очевидное свойство, так как каждое положительное число имеет логарифм по основанию а.D(f)=R+
2. Областью значения логарифмической функции будет являться все множество действительных чисел.E(f)= (-∞; +∞)
3. График логарифмической функции всегда проходит через точку (1;0).
4.Ллогарифмическая функция возрастает при а>1, и убывает при 0<х<1.
5. Функция не является четной или нечетной. Логарифмическая функция – функция общего вида.
6. Функция не имеет точек максимума и минимума, в области определения непрерывна.
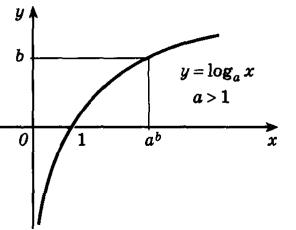
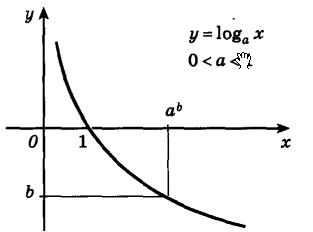
На следующем рисунке представлен график убывающей логарифмической функции - (0
Если построить в одной оси координат показательную и логарифмическую функции с одинаковыми основаниями, то графики этих функций будут симметричны относительно прямой y = x. Данное утверждение показано на следующем рисунке.
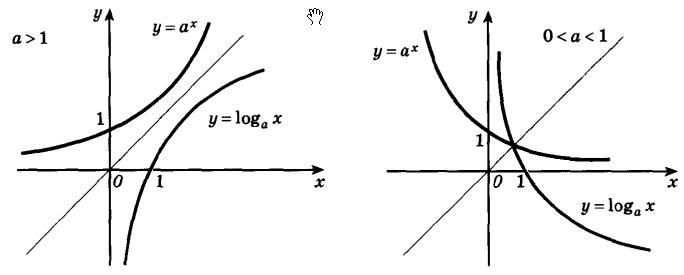
Изложенное выше утверждение будет справедливо, как для возрастающих, так и для убывающих логарифмических и показательных функций.
Рассмотрим пример: найти область определения логарифмической функции f(x) = log8(4 - 5x).
Исходя из свойств логарифмической функции, областью определения является все множество положительных действительных чисел R+. Тогда заданная функция будет определена для таких х, при которых 4 - 5x>0. Решаем это неравенство и получаем x<0.8. Таким образом, получается, что областью определения функции f(x) = log8(4 - 5*x) будет являться промежуток (-∞;0.8)
Графики логарифмической функции в программе GeoGebra
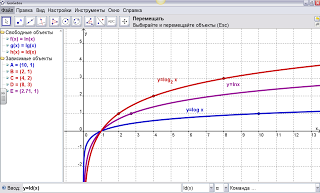
Графики логарифмической функции
1) натуральный логарифм y = ln (x)
2) десятичный логарифм y = lg (x)
3) логарифм по основанию 2 y = ld (x)
V. Закрепление темы
Применяя полученные свойства логарифмической функции решим следующие задания:
1. Найти область определения функции: у=log8(4-5x);у= log0,5(2х+8);.
3. Схематично построить графики функций:у=log2(х+2) -3 у= log2(х) +2
Подводятся итоги урока: Рефлексия в форме диалога:
«На уроке я работал активно / пассивно»
«Совей работой на уроке я доволен / не доволен»
«Урок мне показался коротким / длинным»
«Я не достиг хорошего результата потому, что …»
«Материал урока мне был понятен / не понятен»
«Моё настроение стало лучше / хуже».
Вопросы диктанта
Логарифмическая функция у = logax определена при любом х. (^)
-
Функция у = logax логарифмическая при а>0, а ≠ 1, х>0. ( _ ) -
Областью определения логарифмической функции является множество действительных чисел. (^) -
Областью значений логарифмической функции является множество действительных чисел. ( _ ) -
Логарифмическая функция – четная. (^) -
Логарифмическая функция – нечетная. (^) -
Функция у = logax (при основании большем 1) – возрастающая.( _ ) -
Функция у = logax при положительном, но меньшем единицы основании, - возрастающая. (^) -
Логарифмическая функция имеет экстемум в точке (1; 0). (^) -
График функции у = logax пересекается с осью Ох. ( _ ) -
График логарифмической функции находится в верхней полуплоскости. (^) -
График логарифмической функции симметричен относительно Ох. (^) -
График логарифмической функции всегда находится в I и IV четвертях. ( _ ) -
График логарифмической функции всегда пересекает Ох в точке (1; 0). ( _ ) -
Существует логарифм отрицательного числа. (^) -
Существует логарифм дробного положительного числа.( _ ) -
График логарифмической функции проходит через точку (0; 0). (^)
2. На каком из рисунков изображен график функции
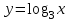. Укажите этот рисунок.
| 1) | 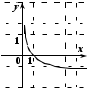 | 2) |  |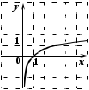
| 3) | 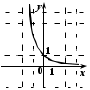 | 4) |  |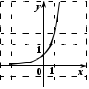
| | |
| | |