Файл: Практическая работа 2 по дисциплине (учебному курсу) Электротехника и электроника.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 36
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М
 ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение
высшего образования
«Тольяттинский государственный университет»
Институт машиностроения
(наименование института полностью)
Кафедра /департамент /центр1 15.03.05 Конструкторскотехнологическое обеспечение машиностроительных производств
(наименование кафедры/департамента/центра полностью)
практическая РАБОТА №2
-
по дисциплине (учебному курсу) «Электротехника и электроника»
(наименование дисциплины (учебного курса)
Вариант ____ (при наличии)
| Студент | Мареськин Сергей Викторович | |
| Группа | ТМбд-2001а | |
| Преподаватель | Тарасов Никита Константинович (И.О. Фамилия) | |
Тольятти 2023
Практическое задание 1
Цель работы – практическое освоение методов расчета электрических цепей постоянного и переменного тока.
Вариант первой задачи определяется двумя цифрами.
Первая цифра соответствует номеру строки в таблице 2.
Вторая цифра соответствует номеру строки исходных данных в таблице 3.
Таблица 1 Формирование варианта задач студента
Таблица 2 Конфигурация расчетной электрической цепи постоянного тока
| № | Расчетная электрическая цепь | ||
| Пункт задания 1.1 | Пункт задания 1.2 | ||
| 1 |  | 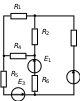 | R3 E2 |
Таблица 3 Параметры электрической цепи постоянного тока
| № | 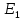 , , В | Е2, В | Е3, В | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом |
| 9 | 180 | 170 | 190 | 220 | 240 | 120 | 130 | 170 | 250 |
1.1. Преобразование цепи
Найти величину эквивалентного сопротивления цепи, преобразовав электрическую цепь, заданную первой цифрой варианта (табл. 2). Величины сопротивлений резисторов – согласно таблице 3.
Решение

Данную электрическую цепь можно преобразовать:
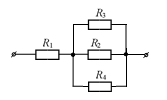
Эквивалентное сопротивление цепи
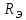 находится по формуле:
находится по формуле: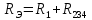
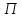 ри этом, общее сопротивление паралельно соединённых сопротивлений
ри этом, общее сопротивление паралельно соединённых сопротивлений 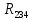 находится по формуле:
находится по формуле: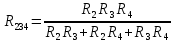
Тогда:
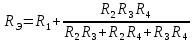
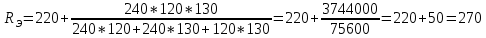 (Ом)
(Ом) Ответ
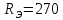 (Ом)
(Ом) 1.2. Расчет неизвестных токов по законам Кирхгофа
В этом пункте необходимо составить систему уравнений по I и II законам Кирхгофа для электрической цепи
, заданной первой цифрой варианта (табл.
2). Рассчитать токи любым известным вам способом.
Составить уравнение баланса мощностей. Удостовериться в правильности расчета токов ветвей. Определить погрешность баланса мощностей.
Рассчитать потенциалы точек для внешнего контура (табл. 2) и построить потенциальную диаграмму.
Решение
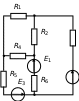 | R3 E2 |
Метод узловых и контурных уравнений основан на применении первого и второго законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчета любой цепи.
При расчете данным методом произвольно задаем направление токов в ветвях.
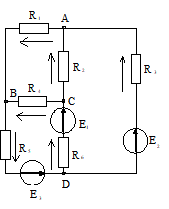
Составляем систему уравнений. В системе должно быть столько уравнений, сколько в цепи ветвей (неизвестных токов).
В заданной цепи 6 ветвей, значит, в системе должно быть 6 уравнений (т = 6). Сначала составляем уравнения для узлов по первому закону Кирхгофа. Для цепи с п узлами можно составить (n-1) независимых уравнений. В нашей цепи 4 узла (А, В, С, D), значит, число уравнений: n-1=4-1=3. Составляем 3 уравнения для любых 3-х узлов, например, для узлов А, В, C.
Задаемся обходом каждого контура и составляем уравнения по второму закону Кирхгофа.
А: I1=I2+ I3
B: I5=I1+ I4
C: I6=I2+ I4
Контур АВCА – обход против часовой стрелки
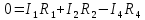
Контур BDCB - обход против часовой стрелки
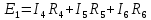
Контур DACD - обход против часовой стрелки
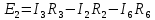
Мы получили систему из 6 уравнений с 6 неизвестными:
I1=I2+ I3
I5=I1+ I4
I6=I2+ I4
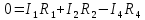
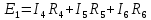
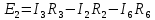
Подставляем в уравнение численные значения
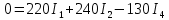
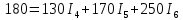
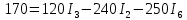
Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на n-1.
Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока — контурного тока, являющегося расчетной величиной.
В заданной можно рассмотреть три контура-ячейки (ABCA, BDCB, DACD) и ввести для них контурные токи Ik1, Ik2, Ik3.
Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.
При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура.
На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим:
стрелками указываем выбранные направления контурных токов Ik1, Ik2, Ik3 в контурах-ячейках. Направление обхода контуров принимаем таким же;
составляем уравнения и решаем систему уравнений или методом
подстановки, или с помощью определителей.
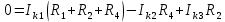
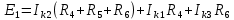
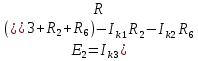
Подставляем в уравнение численные значения ЭДС и сопротивлений.
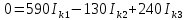
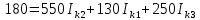
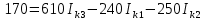
Решим систему с помощью определителей. Вычислим определитель системы ∆ и частные определители ∆1, ∆2, ∆3
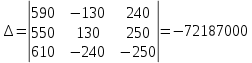
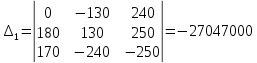
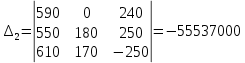
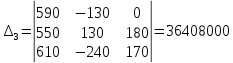
Вычисляем контурные токи:
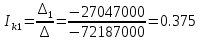 (A)
(A)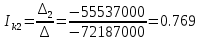 (A)
(A)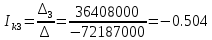 (A)
(A)Действительные токи ветвей:
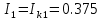 (A)
(A)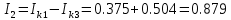 (A)
(A)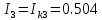 (A)
(A)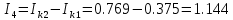 (A)
(A)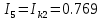 (A)
(A)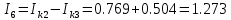 (A)
(A)По методу наложения ток в любом участке цепи рассматривается как алгебраическая сумма частных токов, созданных каждой ЭДС в отдельности.
а) Определяем частные токи от ЭДС Е1 при отсутствии ЭДС Е2 и Е3 т. е. рассчитываем цепь по
Показываем направление частных токов от ЭДС E1 и обозначаем буквой I с одним штрихом (I'). Решаем задачу методом "свертывания"
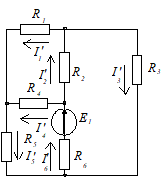
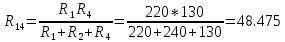 (Ом)
(Ом)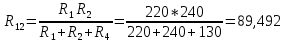 (Ом)
(Ом)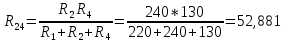 (Ом)
(Ом)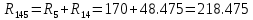 (Ом)
(Ом)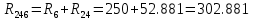 (Ом)
(Ом)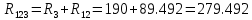 (Ом)
(Ом)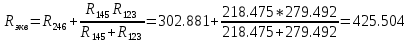 (Ом)
(Ом)Ток источника
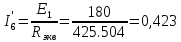 (А)
(А)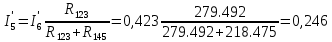 (A)
(A)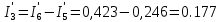 (A)
(A)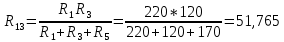 (Ом)
(Ом) 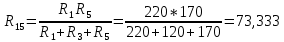 (Ом)
(Ом) 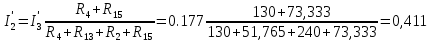 (A)
(A)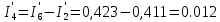 (A)
(A)