Файл: Основные теоретические сведения. Движением называется преобразование, при котором сохраняются расстояния между точками.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 45
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое занятие. Движение в пространстве
Виды симметрий в пространстве. Симметрия многогранников.
Цель работы: Рассмотреть виды симметрий в пространстве и многогранников; выполнить задания практической работы.
Основные теоретические сведения.
Движением называется преобразование, при котором сохраняются расстояния между точками.
Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что|AB|=|A1B1|.
При движении в пространстве
- прямые переходят в прямые,
- полупрямые — в полупрямые,
- отрезки — в отрезки,
- сохраняются углы между прямыми.
Виды движения в пространстве
| 1. Центральная симметрия (симметрия относительно точки): 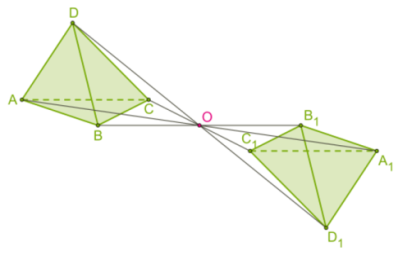 | 2. Осевая симметрия (симметрия относительно прямой): 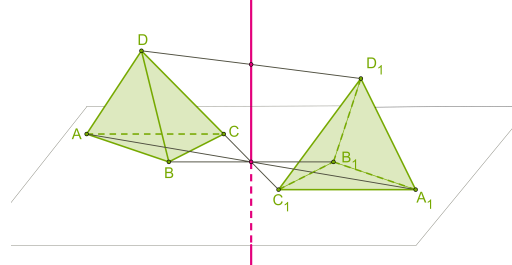 |
| 3. Зеркальная симметрия (симметрия относительно плоскости): 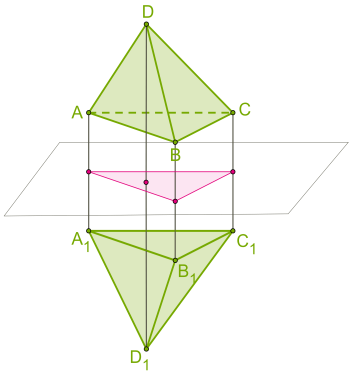 | 4. Параллельный перенос (точки переносятся на данный вектор): 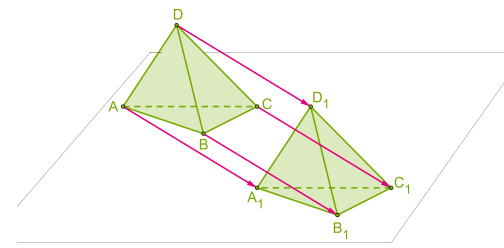 |
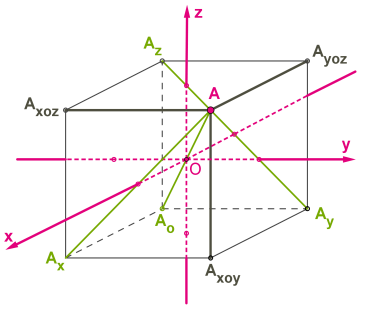 | Пример 1.Если в этой координатной системе дана точка A(1;8;10), то в… 1. …центральной симметрии относительно начала координат точка A переходит в точку A0(−1;−8;−10). 2. …осевой симметрии относительно оси Ox точка A переходит в точку Ax(1;−8;−10). оси Oy точка A переходит в точку Ay(−1;8;−10). оси Oz точка A переходит в точку Az(−1;−8;10). 3. …в зеркальной симметрии относительно координатной плоскости (xOy) точка A переходит в точку Axoy(1;8;−10). координатной плоскости (yOz) точка A переходит в точку Ayoz(−1;8;10). координатной плоскости (xOz) точка A переходит в точку Axoz(1;−8;10). |
Симметрия – это закономерная повторяемость элементов (или частей) фигуры или какого-либо тела, при которой фигура совмещается сама с собой при некоторых преобразованиях (вращение вокруг оси, отражение в плоскости).
Понятие симметрии включает в себя такие понятия, как: ось симметрии, центр симметрии и плоскость симметрии.
1) Ось симметрии - воображаемая ось, при повороте вокруг которой на некоторый угол, фигура совмещается сама с собой в пространстве (
2) Центр симметрии - это точка внутри многогранника, в которой пересекаются и делятся пополам прямые, соединяющие одинаковые элементы многогранника (грани, рёбра, углы) (С).
3) Плоскость симметрии делит многогранник на 2 зеркально равные части (Р).
Симметрия в кубе.
| а) Центр симметрии (центр куба) - точка пресечения диагоналей куба. | 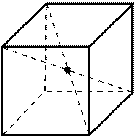 |
| б) Плоскости симметрии (9): 1) 3 плоскости симметрии, проходящие через середины параллельных ребер; 2) 6 плоскостей симметрии, проходящие через противолежащие ребра. | 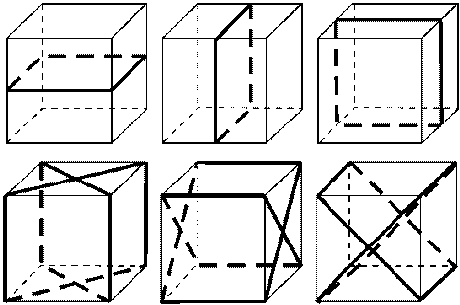 |
| в) Оси симметрии (13): 1)3 оси, проходящие через центры противолежащих граней; 2) 4 оси симметрии, проходящие через противолежащие вершины; 3) 6 осей, проходящие через середины противолежащих рёбер. | 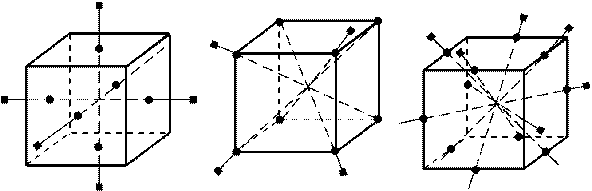 |
Симметрия в параллелепипеде.
| а) Центр симметрии - точка пересечения диагоналей прямоугольного параллелепипеда. | 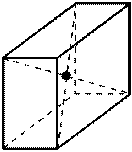 |
| б) Плоскость симметрии. 3 плоскости симметрии, проходящие через середины параллельных рёбер. | 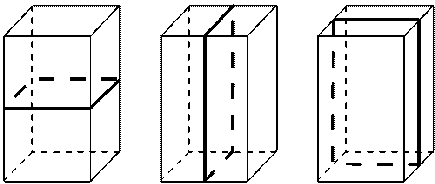 |
| в) Оси симметрии. 3 оси симметрии, проходящие через точки пересечения диагоналей противолежащих граней | 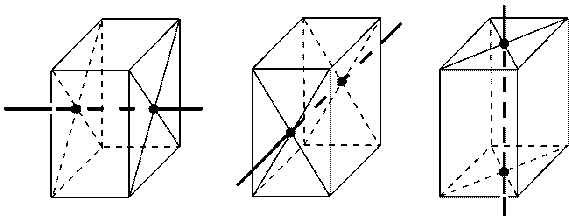 |
Симметрия в призме
| 1) Симметрия прямой призмы. Одна плоскость симметрии, проходящая через середины боковых рёбер. | 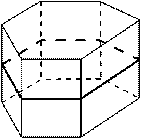 |
| 2) Симметрия правильной призмы. а) Центр симметрии. При чётном числе сторон основания центр симметрии - это точка пересечения диагоналей правильной призмы. | 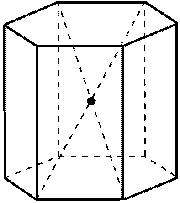 |
| б) Плоскости симметрии: 1) плоскость, проходящая через середины боковых рёбер; 2) при чётном числе сторон основания - плоскости, проходящие через противолежащие рёбра. | 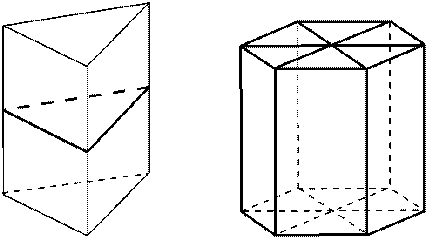 |
| в) Ось симметрии: а) при чётном числе сторон основания - ось симметрии проходит через центры оснований; б) оси симметрии, проходящие через точки пресечения диагоналей противолежащих боковых граней. | 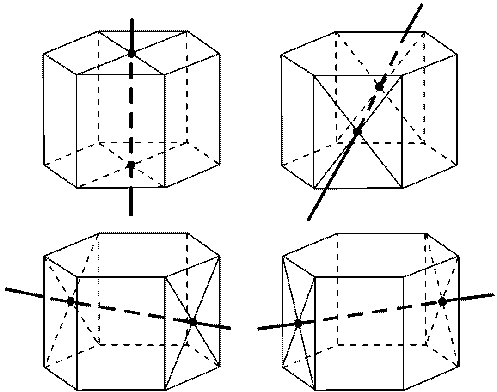  |
Симметрия в пирамиде
| а) Плоскости симметрии: при четном числе сторон основания — а) плоскости, проходящие через противолежащие боковые ребра, и б) плоскости, проходящие через медианы, проведенные к основанию противолежащих боковых граней. | 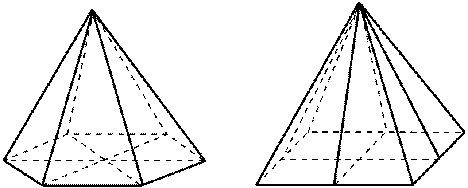 |
| б) Ось симметрии: при четном числе сторон основания — ось симметрии проходит через вершину правильной пирамиды и центр основания. | 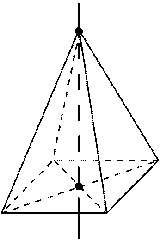 |
Задания для выполнения по вариантам
ВНИМАНИЕ. ТЕКСТ ЗАДАНИЯ И ПОДРОБНОЕ РЕШЕНИЕ ПИШЕМ В ТЕТРАДЬ
| Вариант 1 | Вариант 2 | |
| I.В координатной системе дана точка A(2;11;16). Определи координаты точек, в которые переходит точка A в… 1. …центральной симметрии относительно начала координат:  ; ; ; ; 2. …осевой симметрии относительно оси Ox:  ; ; ; ; оси Oy:  ; ; ; ; оси Oz:  ; ; ; ; 3 …в зеркальной симметрии относительно координатной плоскости (xOy):  ; ; ; ; координатной плоскости (yOz):  ; ; ; ; координатной плоскости (xOz):  ; ; ; ; | I.В координатной системе дана точка A(11;4;4). Определи координаты точек, в которые переходит точка A в… 1. …центральной симметрии относительно начала координат:  ; ; ; ; 2. …осевой симметрии относительно оси Ox:  ; ; ; ; оси Oy:  ; ; ; ; оси Oz:  ; ; ; ; 3 …в зеркальной симметрии относительно координатной плоскости (xOy):  ; ; ; ; координатной плоскости (yOz):  ; ; ; ; координатной плоскости (xOz):  ; ; ; ; | |
| II.Дан куб ABCDA1B1C1D1. 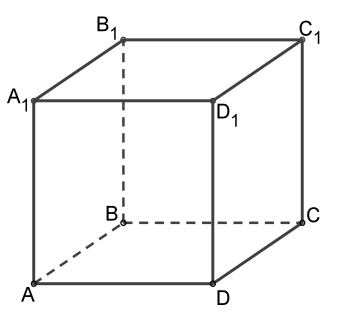 1. С помощью каких движений вершиныB,B1,C1,C переходят соответственно в вершины A,A1,D1,D?
2. С помощью каких движений вершиныA1,B1,C1,D1 переходят соответственно в вершины C,D,A,B?
3. С помощью каких движений вершиныA,B,C,D переходят соответственно в вершины C,B,A,D?
| II.Дан куб ABCDA1B1C1D1.  1. С помощью каких движений вершиныB,B1,C1,C переходят соответственно в вершины A,A1,D1,D?
2. С помощью каких движений вершиныA,A1,B1,B переходят соответственно в вершины C1,C,D,D1?
3. С помощью каких движений вершиныD,D1,C1,C переходят соответственно в вершины C1,D1,D,C?
| |
| Начало формы III.Дан правильный тетраэдр DABC.  1. С помощью каких движений вершины (ABD) переходят соответственно в вершины A,C,B,D?
2. С помощью каких движений все точки грани (ABD) переходят в точки этой же грани (грань отображается на себя)?
| III.Дан правильный тетраэдр DABC.  1. С помощью каких движений вершины (ACD) переходят соответственно в вершины A,C,B,D?
2. С помощью каких движений все точки грани (ACD) переходят в точки этой же грани (грань отображается на себя)?
| |
| Начало формы IV.Точка A(−3;−8;−8) в центральной симметрии относительно центра C переходит в точку B(1;4;1). Определи координаты точки C . Ответ: C(  ; ; ; ; )Конец формы )Конец формы | IV.Точка A(−2;9;1) в центральной симметрии относительно центра C переходит в точку B(1;−3;−1). Определи координаты точки C . Ответ: C(  ; ; ; ; ) ) | |
| 2. Сколько плоскостей симметрии имеет октаэдр?  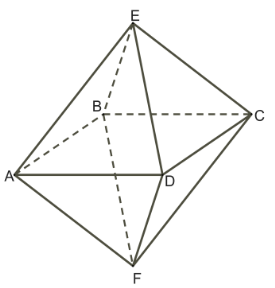 | 2. Сколько плоскостей симметрии имеет правильная четырёхугольная призма?  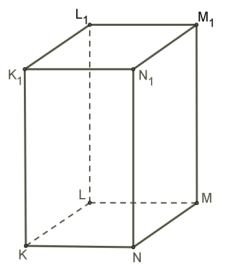 | |
| 1. При каких движениях октаэдр отображается на себя (все точки многогранника переходят в точки этого же многогранника)? 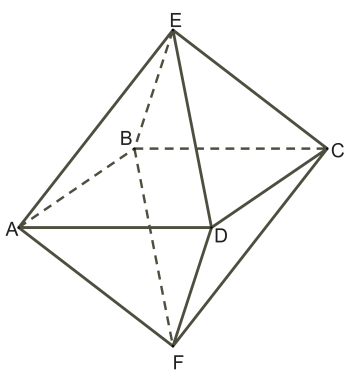
| 2. Сколько плоскостей симметрии имеет правильная четырёхугольная пирамида?  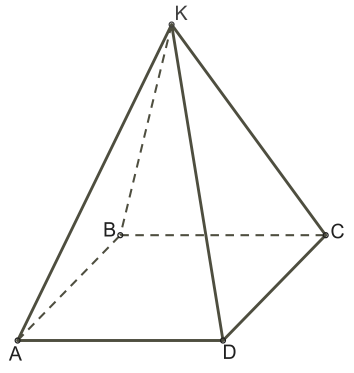 | |
 симметрия относительно оси
симметрия относительно оси все названные движения
все названные движения