Файл: Потери давления в трубопроводе при турбулентном течении неустойчивых эмульсий.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 47
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лекция 2
ПОТЕРИ ДАВЛЕНИЯ В ТРУБОПРОВОДЕ ПРИ
ТУРБУЛЕНТНОМ ТЕЧЕНИИ НЕУСТОЙЧИВЫХ ЭМУЛЬСИЙ
Известно, что на нефтяных месторождениях страны широкое распространение получила внутритрубопроводная деэмульсация нефти, которая оказалась эффективным методом промысловой подготовки нефти, в ряде случаев полностью заменяющим подготовку ее на специальных установках
При введении деэмульгатора в турбулентный поток обводненной нефти в трубопроводе происходят интенсивное разрушение бронирующих оболочек на глобулах пластовой воды и укрупнение незащищенных глобул в десятки и сотни раз. В результате этого в трубопроводе появляется неустойчивая макроэмульсия, которая существует под действием турбулентных пульсаций одной жидкости на другую и легко расслаивается на нефть и воду при ламинарном режиме течения или в отстойных резервуарах.
Транспортировка неустойчивых эмульсий осуществляется зачастую на значительные расстояния, достигающие 100 км. При расчете трубопроводов, транспортирующих нефтяные эмульсии ,коэффициент гидравлического сопротивления определяется обычно по формуле Блазиуса с подстановкой в число Рейнольдса плотности эмульсии и ее эффективной вязкости .
Для неустойчивых грубодисперсных эмульсий такой подход не учитывает влияния глобул дисперсной фазы на интенсивность турбулентности дисперсионной среды, что приводит к существенному завышению расчетных коэффициентов гидравлического сопротивления и к росту капитальных затрат при строительстве трубопроводов .
Ранее авторами были получены расчетные формулы для определения коэффициента гидравлического сопротивления при турбулентном течении разбавленных эмульсий* в зоне гладкостенного сопротивления. При выводе этих зависимостей диаметр глобул эмульсии определяли по формуле А.Н. Колмогорова. Однако, это допущение применимо лишь в первом приближении, так как указанная формула устанавливает зависимость критического (максимального) диаметра глобул от основных параметров потока. Под разбавленной эмульсией понимается такая, в которой глобулы дисперсной фазы могут свободно перемещаться относительно друг друга и с содержанием дисперсной фазы <0,524.
Формулы для определения коэффициента гидравлического сопротивления э при турбулентном течении неустойчивых эмульсий принимают следующий вид:
 (1)
(1)Где -средняя скорость течения эмульсий в трубопороводе, э и с –динамическая вязкость эмульсии и дисперсионной среды, э, с, ф –плотность эмульсии, дисперсионной среды и дисперсной фазы, -межфазное натяжение, -объемная доля дисперсной фазы, D-внутренний диаметр трубы, 0- безразмерная толщина ламинарного подслоя
Динамическая вязкость неустойчивой эмульсии определяется по уравнению Бринкмана
mэ=mс(1-b)-2,5 (2)
На основании реологических исследований показана применимость уравнения (2) при скоростях сдвига Vc<100 /с. В реальных промысловых трубопроводах скорость сдвига не бывает выше указанного предела. В этих условиях деформация глобул дисперсной фазы незначительна и не приводит к возникновению дополнительного напряжения сдвига и проявлению неньютоновского поведения неустойчивых эмульсий .
Глобулы диспергированной жидкости оказывают влияние на турбулентную кинематическую вязкость, что проявляется в уменьшении участка смешения по сравнению с турбулентным течением однофазной жидкости. Это обусловливается прежде всего уменьшением объема, в котором происходит диссипация турбулентной энергии, поскольку пленка поверхностно-активных веществ, адсорбируемых на поверхности раздела жидкостей, препятствует проникновению пульсационных движений внутрь глобул. Кроме того, вследствие превышения размеров капелек изучаемых эмульсий внутреннего масштаба турбулентности дисперсионной среды происходит гашение турбулентных пульсаций дисперсионной среды на поверхности капелек.
ствует проникновению пульсационных движений внутрь глобул. Кроме того, вследствие превышения размеров капелек изучаемых эмульсий внутреннего масштаба турбулентности дисперсионной среды происходит гашение турбулентных пульсаций дисперсионной среды на поверхности капелек.
Влияние этих двух факторов на величину коэффициента гидравлического сопротивления растет с увеличением содержания дисперсной фазы и степени дисперсности эмульсии. В результате этого при развитом турбулентном режиме течения по трубопроводу неустойчивых эмульсий имеет место снижение удельных потерь давления при возрастании содержания дисперсной фазы, несмотря на рост коэффициента динамической вязкости эмульсии по сравнению с вязкостью нефти.
Полученные с учетом этого явления формулы Медведева В.Д., Гужова А.И., Медведева Л.П. дают существенно меньшие значения э нежели расчет по Блазиусу
lэ = 0,3164/Reэ 0,25 (3)
который рекомендуется в некоторых работах для определения гидравлических сопротивлений при течении эмульсий в трубах.
На рис. 1 приведена зависимость удельных потерь давления от содержания дисперсной фазы. Опытные точки сопоставляются с расчетными по формулам (1 и 3). Видно, что расчет потерь давления с определением э, по Блазиусу существенно превышает опытные значения удельных потерь давления (при = 0,40,5 расхождение достигает 45%). В то же время отклонение опытных точек от расчетной кривой с определением э по (1) не превышает ± 6%. Это позволяет рекомендовать формулы для гидравлического расчета трубопроводов, транспортирующих неустойчивые эмульсии при внутритрубной деэмульсации нефти.

Рис. 1. Зависимость удельных потерь давления от содержания дисперсной фазы
при см равных 1,7(1) и 1,3 м/с (2)
Расчетные 3 - по формуле (1); 4 - по Блазиусу.
Компьютерное моделирование процесса расслоения эмульсии в трубопроводе
При проектировании систем нефтегазосбора с применением внутритрубной деэмульсации правильно подобранный диаметр трубопровода (в дальнейшем называемый рациональным) должен обеспечивать разрушение бронирующих оболочек и укрупнение капель до размера, при котором будет эффективно работать отстойная аппаратура. В тоже время этот диаметр должен быть таким, чтобы в трубопроводе, когда это нежелательно, не возникало расслоения потока. Формально выбор рационального диаметра трубопровода мог бы быть осуществлен с помощью диаграмм структур потока, полученных для лабораторных условий. Однако, области значений чисел Рейнольдса, Вебера и Фруда, соответствующих лабораторным и промысловым условиям, не перекрываются и перенос результатов оказывается проблематичным.
В работах [198, 200] для монодисперсных эмульсий предложен метод расчета труб из условия, что расслоение потока возникает в тех случаях, когда скорость седиментации капель оказывается равной или выше среднеквадратичной пульсационной скорости. Метод дает приемлемые значения диаметра трубопровода и применяется на нефтяных промыслах
, где подготовка продукции скважин ведется по совмещенной технологии с использованием трубной деэмульсации. Однако этот метод не учитывает полидисперсности и степени обводненности эмульсии. Кроме того, как это будет показано, даже статические условия возникновения расслоения эмульсии не совсем верно отвечают реальной динамической картине формирования структуры потока, в том числе перехода его из эмульсионного в расслоенное состояние. Метод отражает картину только предельных состояний, исключая промежуточные: движение в трубе жидкости в виде эмульсии или же полностью расслоенного потока. В дальнейшем метод был модифицирован в работе [200], где концентрация дисперсной фазы была учтена косвенным образом через коэффициент гидравлического сопротивления. Поскольку допущения и основа метода расчета остались неизменными, то результаты и в этом случае остаются не адекватны реальным.
В работе изложены результаты компьютерного моделирования процесса расслоения в трубопроводе. Для этого была построена динамическая модель движения эмульсии, которая с учетом полидисперсности описывает изменение распределения капель дисперсной фазы но размерам (РКР), обусловленное процессами турбулентной диффузии и седиментации. Процессы дробления и коалесценции учтены путем задания исходного эмпирического РКР.
Модель седиментационно-турбулентного равновесия. Диффузионные процессы являются выравнивающими. Гравитационный эффект относится к разделяющим. Совместное действие столь противоположных по конечному результату механизмов приводит к известному явлению изменения числа частиц в объеме по высоте.
Для количественного описания явления целесообразно использовать методологию работы , разработанную для коллоидных систем.
Согласно первому закону Фика, диффузионный поток частиц дисперсной фазы, принадлежащих к i-й фракции (интервал размеров i и i-
где: DТ- коэффициент турбулентной диффузии; n- число частиц i-й фракции в единице объема; у - ось, направленная вверх для случая более тяжелой дисперсной фазы и вниз, если она легче сплошной фазы.
Тогда седиментационный поток частиц может быть отражен выражением (2):
где: v i - скорость седиментации частиц i-й фракции.
Условие динамического равновесия наступает тогда, когда J d i =JsiЭто позволяет придти к обыкновенному дифференциальному уравнению первого порядка (3)
Предполагая в 1-м приближении, что величины vi, Diне зависят от у, после интегрирования получим следующее выражение для численной концентрации i-й фракции (4):

Если принять, что до начала установления седиментационно-турбулентного равновесия распределение частиц от высоты не зависит и, обозначив через ni исходную численную концентрацию для i-й фракции, а через Н - размер области, занятой дисперсной системой по оси у, получим уравнение баланса по дисперсной фазе до и после установления равновесия для столба эмульсии высотой Н и единичного сечения в виде [5].
Учитывая (4), связь неизвестной величины пi (0) с исходной численной концентрацией ni определяется выражением (6)
Переход к расслоенному течению произойдет, если величина концентрации дисперсной фазы на дне сосуда или трубопровода, т.е. при у = 0, достигнет критического значения W*. Поскольку объемная концентрация связана с численным соотношением (7)
где: 32i - саутеровский диаметр для частиц i-й фракции, то, суммируя (6) по фракциям с учетом (7), оказывается справедливым следующее выражение для условий перехода к расслоенному течению (8):
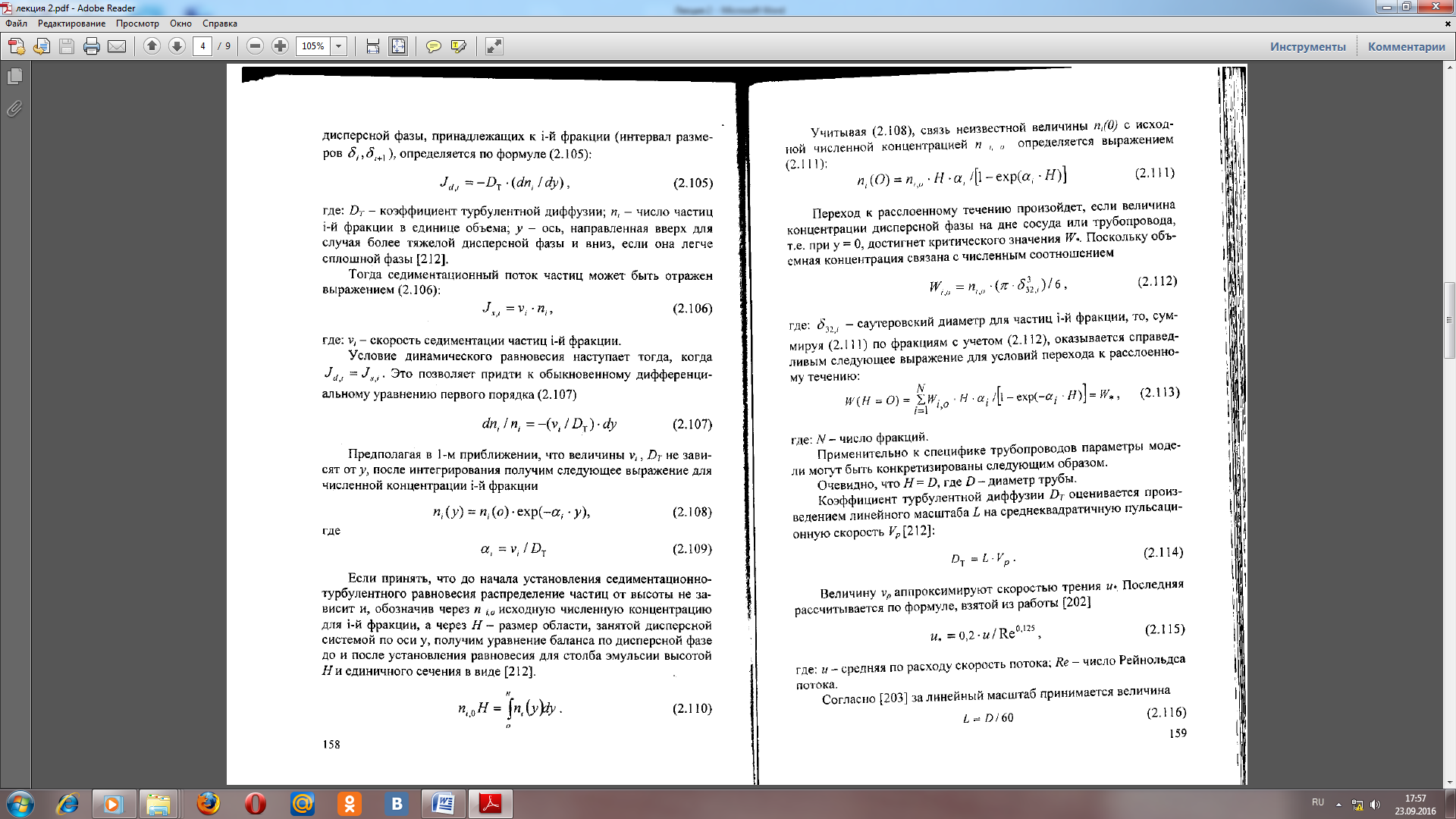
где: N - число фракций.
Применительно к специфике трубопроводов параметры модели могут быть конкретизированы следующим образом.
Очевидно, что Н= D, где D - диаметр трубы.
Коэффициент турбулентной диффузии DTоценивается произведением линейного масштаба L на среднеквадратичную пульсационную скорость Vp(9):
DT = LVp
Величину vp аппроксимируют скоростью трения и