Файл: Потери давления в трубопроводе при турбулентном течении неустойчивых эмульсий.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 48
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.

где: и - средняя по расходу скорость потока; Re - число Рейнольдса потока.
За линейный масштаб принимается величина L = D/60
Скорость седиментации определяется по формуле Стокса (11)
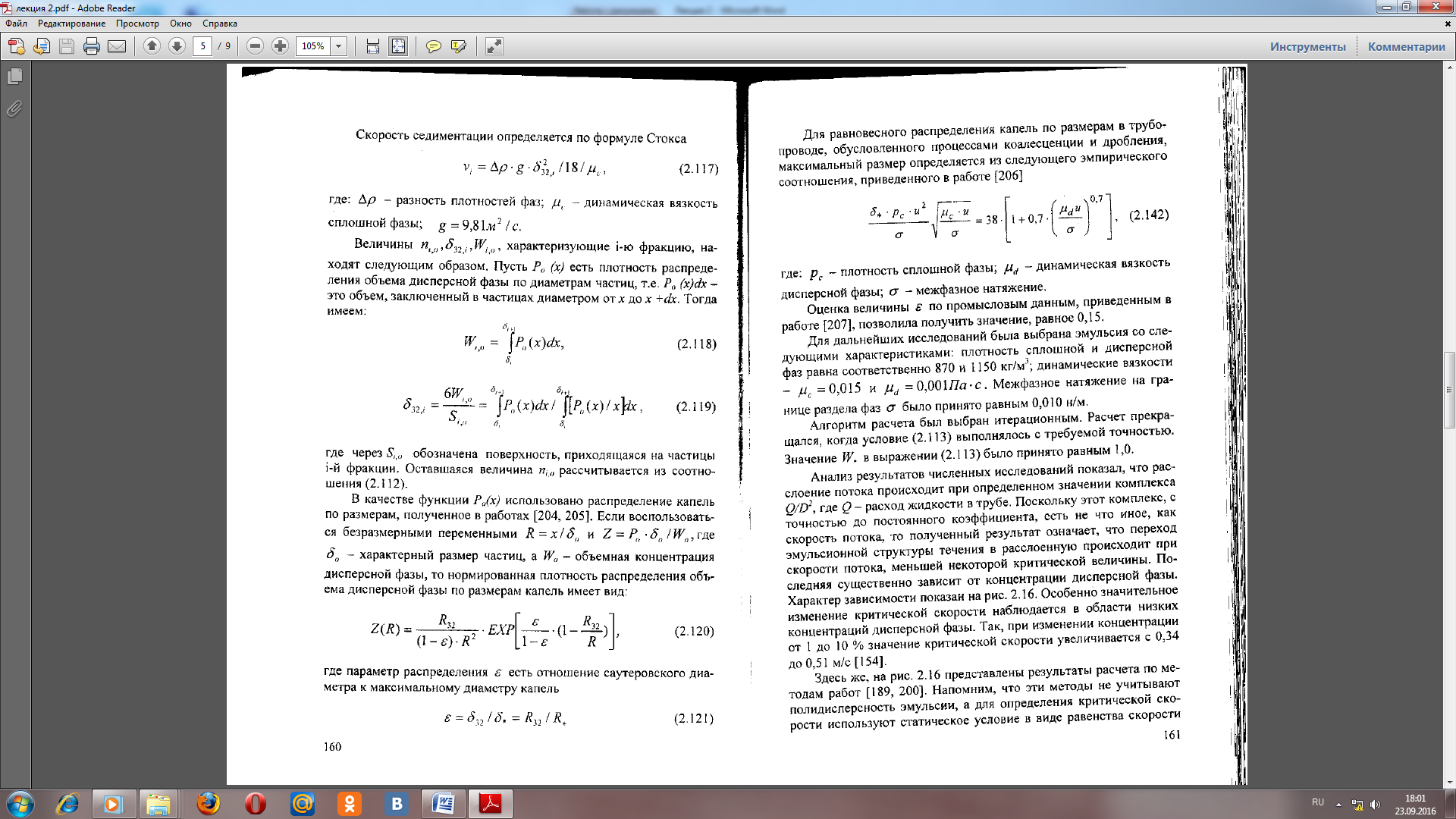
где: - разность плотностей фаз; - динамическая вязкость сплошной фазы
Величины ni,32i, Wi характеризующие i-ю фракцию, находят следующим образом. Пусть
Р0 (х) есть плотность распределения объема дисперсной фазы по диаметрам частиц, т.е.
Р0 (x)dx -это объем, заключенный в частицах диаметром от х до х +dx. Тогда имеем (12):

где через Si0обозначена поверхность, приходящаяся на частицы i-й фракции. Оставшаяся величина рассчитывается из соотношения (7).
В качестве функции Р0(х) использовано распределение капель по размерам. Если воспользоваться безразмерными переменными R = x/0и Z =P00/W0, где0 - характерный размер частиц, a W0- объемная концентрация дисперсной фазы, то нормированная плотность распределения объема дисперсной фазы по размерам капель имеет вид (13):

где параметр распределения есть отношение саутеровского диаметра к максимальному диаметру капель (14):

Для равновесного распределения капель по размерам в трубопроводе, обусловленного процессами коалесценции и дробления, максимальный размер определяется из следующего эмпирического соотношения:

с-плотность сплошной фазы; - динамическая вязкость дисперсной фазы; - межфазное натяжение.
Оценка величины по промысловым данным позволила получить значение, равное 0,15.
Для дальнейших исследований была выбрана эмульсия со следующими характеристиками: плотность сплошной и дисперсной фаз равна соответственно 870 и 1150 кг/м3; динамические вязкости 0,015 и 0,00 мПас. Межфазное натяжение на границе раздела фаз было принято равным 0,010 н/м.
Алгоритм расчета был выбран итерационным. Расчет прекращался, когда условие (8) выполнялось с требуемой точностью. Значение W, в выражении (8) было принято равным 1,0.
Анализ результатов численных исследований показал, что расслоение потока происходит при определенном значении комплекса Q/D2, где Q - расход жидкости в трубе.
Поскольку этот комплекс, с точностью до постоянного коэффициента, есть не что иное, как скорость потока, то полученный результат означает, что переход эмульсионной структуры течения в расслоенную происходит при скорости потока, меньшей некоторой критической величины. Последняя существенно зависит от концентрации дисперсной фазы.
Характер зависимости показан на рис. 1. Особенно значительное изменение критической скорости наблюдается в области низких концентраций дисперсной фазы. Так, при изменении концентрации от 1 до 10 % значение критической скорости увеличивается с 0,34 до 0,51 м/с .
Здесь же, на рис. 1 представлены результаты расчета по методам работ [189, 200]. Напомним, что эти методы не учитывают полидисперсность эмульсии, а для определения критической скорости используют статическое условие в виде равенства скорости седиментации капель среднеквадратичной скорости турбулентных пульсаций.
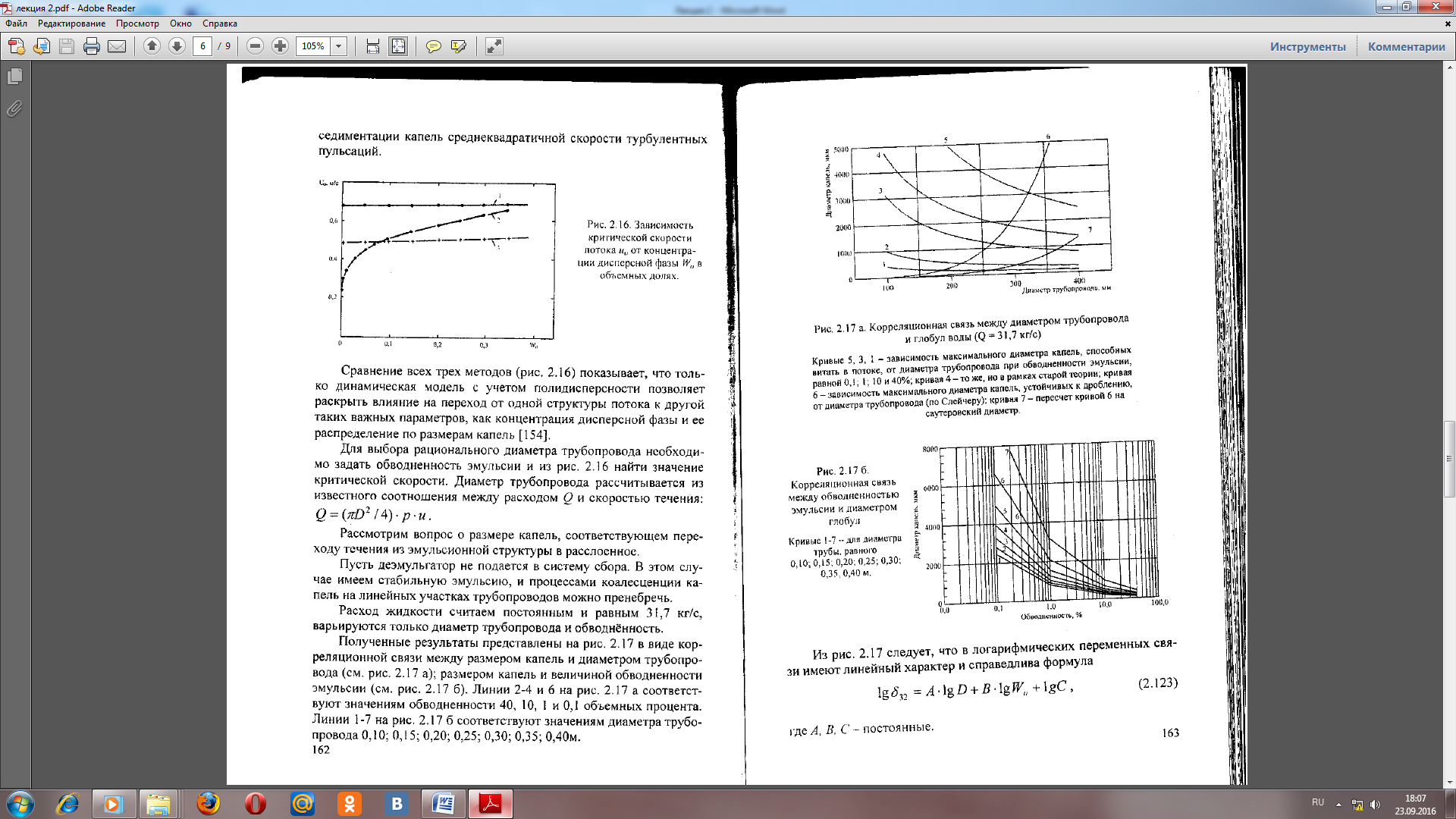
Рис. 1. Зависимость критической скорости потока иоот концентрации дисперсной фазы W0 в
объемных единицах
Динамическая модель с учетом полидисперсности позволяет раскрыть влияние на переход от одной структуры потока к другой таких важных параметров, как концентрация дисперсной фазы и ее распределение по размерам капель.
Для выбора рационального диаметра трубопровода необходимо задать обводненность эмульсии и из рис. 1 найти значение критической скорости. Диаметр трубопровода рассчитывается из известного соотношения между расходом Q и скоростью течения:

Рассмотрим вопрос о размере капель, соответствующем переходу течения из эмульсионной структуры в расслоенное.
Пусть деэмульгатор не подается в систему сбора. В этом случае имеем стабильную эмульсию, и процессами коалесценции капель на линейных участках трубопроводов можно пренебречь. Расход жидкости считаем постоянным и равным 31,7 кг/с, варьируются только диаметр трубопровода и обводнённость. Полученные результаты представлены на рис. 2 в виде корреляционной связи между размером капель и диаметром трубопровода (см. рис. 2 а); размером капель и величиной обводненности эмульсии (см. рис. 2 б). Линии 2-4 и 6 на рис. 3а соответствуют значениям обводненности 40, 10, 1 и 0,1 объемных процента.
Линии 1-7 на рис. 3 б соответствуют значениям диаметра трубопровода 0,10; 0,15; 0,20; 0,25; 0,30; 0,35; 0,40.

Рис. 3 а. Корреляционная связь между диаметром трубопровода и глобул воды (Q = 31,7 кг/с)
Кривые 5, 3, 1 - зависимость максимального диаметра капель, способных витать в потоке, от диаметра трубопровода при обводненности эмульсии, равной 0,1; 1; 10 и 40%; кривая 4 - т о же, но в рамках старой теории; кривая 6 - зависимость максимального диаметра капель, устойчивых к дроблению, от диаметра трубопровода (по Слейчеру): кривая 7 - пересчет кривой 6 на саутеровский диаметр.

Рис. 3 б. Корреляционная связь между обводненностью эмульсии и диаметром глобул
Кривые 1-7 - для диаметра трубы, равного 0,10; 0,15; 0,20; 0,25; 0,30;0,35, 0,40 м.
Из рис. 3 следует, что в логарифмических переменных связи имеют линейный характер и справедлива формула (15)
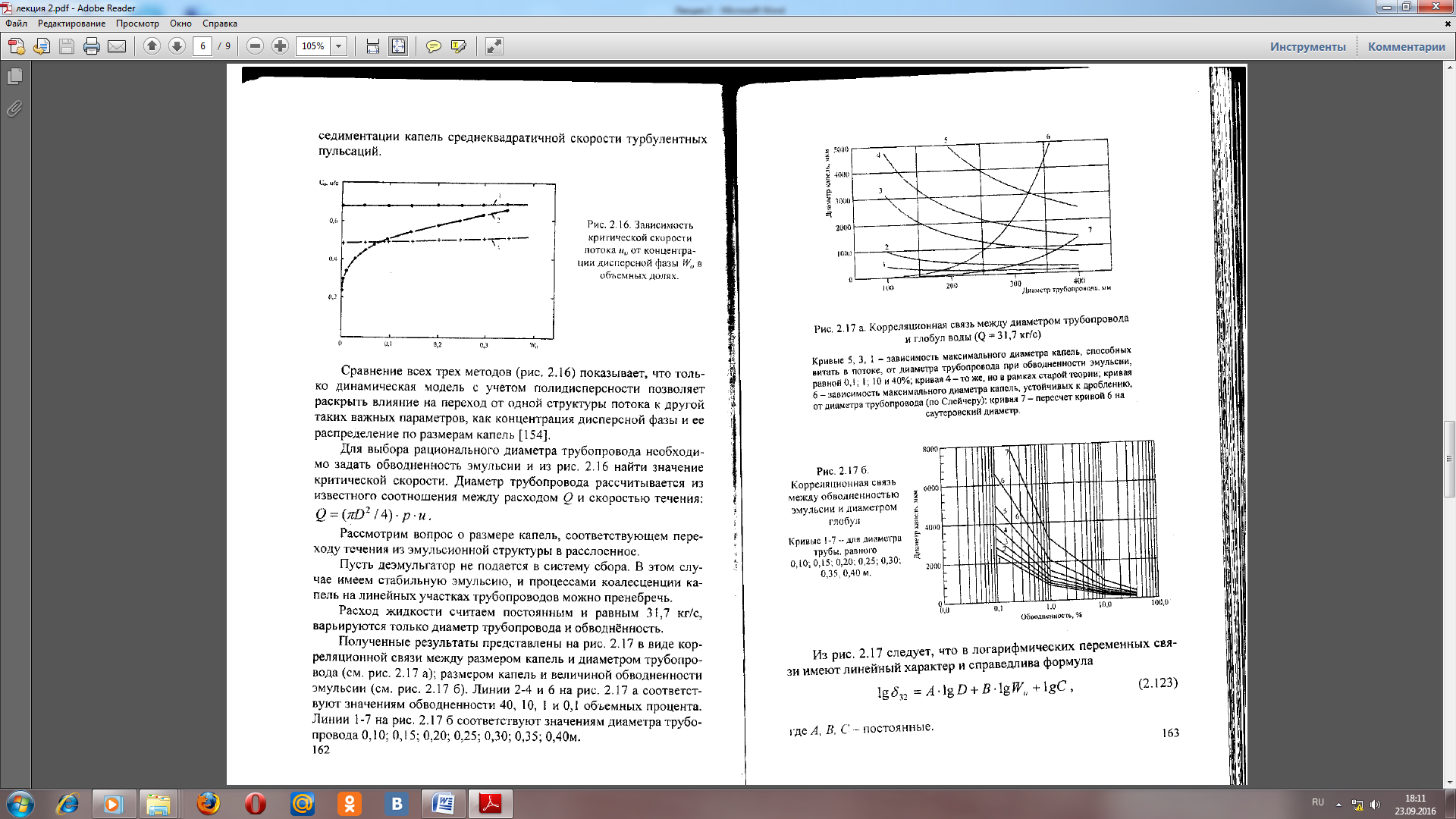
где А, В, С-постоянные.
При А = -1 и В = -0,5 формула приводится к виду (16)
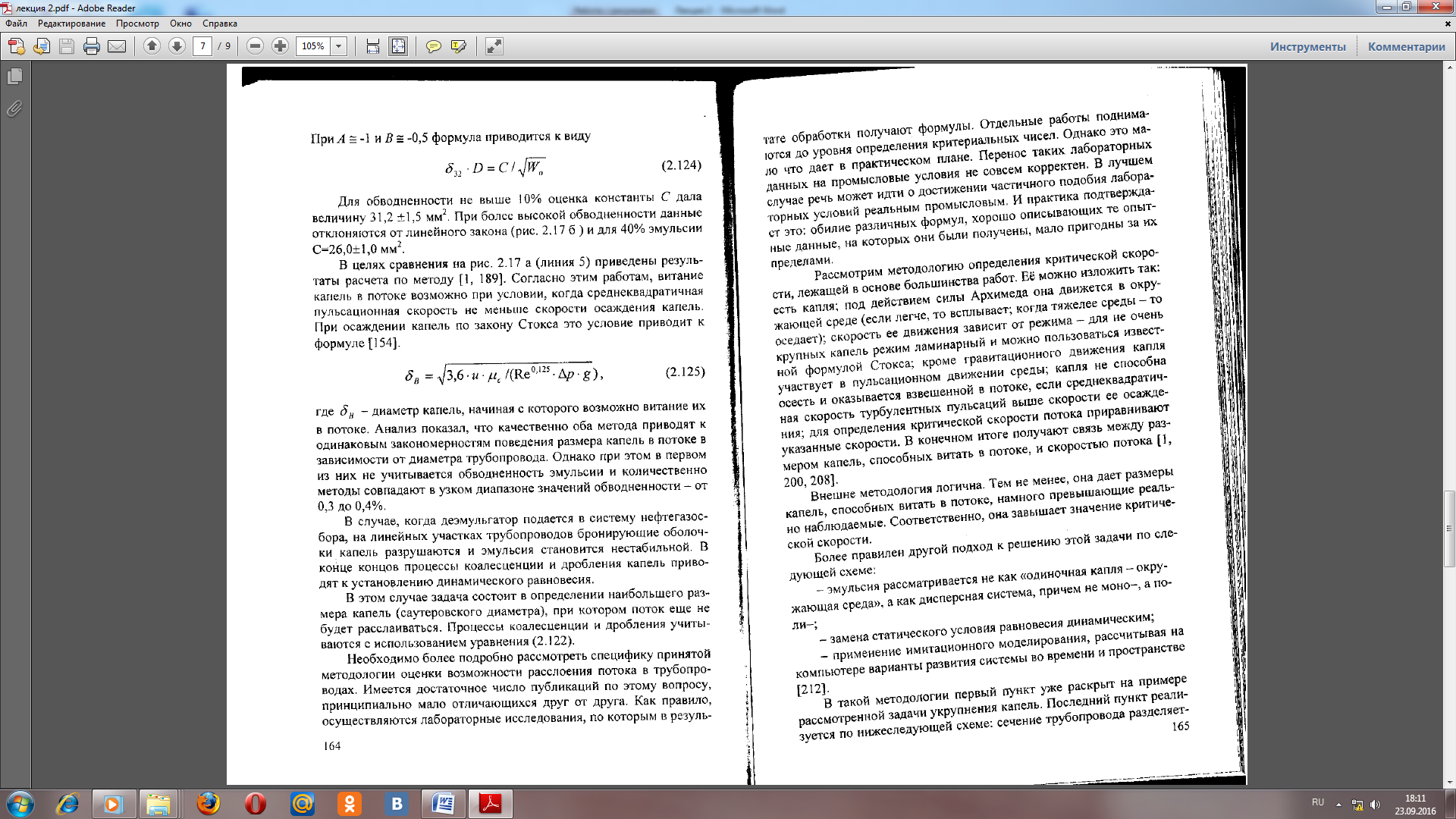
Для обводненности не выше 10% оценка константы С дала величину 31,2 ±1,5 мм2. При более высокой обводненности данные отклоняются от линейного закона (рис. 3 б ) и для 40% эмульсии С=26,0±1,0 мм2.
В случае, когда деэмульгатор подается в систему нефтегазосбора, на линейных участках трубопроводов бронирующие оболочки капель разрушаются и эмульсия становится нестабильной. В конце концов процессы коалесценции и дробления капель приводят к установлению динамического равновесия.
В этом случае задача состоит в определении наибольшего размера капель (саутеровского диаметра), при котором поток еще не будет расслаиваться. Процессы коалесценции и дробления учитываются с использованием уравнения (13).
Необходимо более подробно рассмотреть специфику принятой методологии оценки возможности расслоения потока в трубопроводах. Имеется достаточное число публикаций по этому вопросу, принципиально мало отличающихся друг от друга. Как правило, осуществляются лабораторные исследования, по которым в результате обработки получают формулы. Отдельные работы поднимаются до уровня определения критериальных чисел. Однако это мало что дает в практическом плане. Перенос таких лабораторных данных на промысловые условия не совсем корректен. В лучшем случае речь может идти о достижении частичного подобия лабораторных условий реальным промысловым. И практика подтверждает это: обилие различных формул, хорошо описывающих те опытные данные, на которых они были получены, мало пригодны за их пределами.
Рассмотрим методологию определения критической скорости, лежащей в основе большинства работ. Её можно изложить так: есть капля; под действием силы Архимеда она движется в окружающей среде (если легче, то всплывает; когда тяжелее среды – то оседает); скорость ее движения зависит от режима - для не очень крупных капель режим ламинарный и можно пользоваться известной формулой Стокса; кроме гравитационного движения капля участвует в пульсационном движении среды; капля не способна осесть и оказывается взвешенной в потоке, если среднеквадратичная скорость турбулентных пульсаций выше скорости ее осаждения; для определения критической скорости потока приравнивают указанные скорости. В конечном итоге получают связь между размером капель, способных витать в потоке, и скоростью потока.
Внешне методология логична. Тем не менее, она дает размеры капель, способных витать в потоке, намного превышающие реально наблюдаемые. Соответственно, она завышает значение критической скорости. скорости.
Более правилен другой подход к решению этой задачи по следующей схеме:
- эмульсия рассматривается не как «одиночная капля - окружающая среда», а как дисперсная система, причем не моно-, а поли-;
- замена статического условия равновесия динамическим;
- применение имитационного моделирования, рассчитывая на компьютере варианты развития системы во времени и пространстве.
В такой методологии первый пункт уже раскрыт на примере рассмотренной задачи укрупнения капель. Последний пункт реализуется по нижеследующей схеме: сечение трубопровода разделяется горизонтальными плоскостями от нижней образующей (дно трубы) до верхней на несколько слоев. Их число должно быть достаточно большим, но не настолько, чтобы нарушалось понятие физически малого (элементарного) объема. Под последним имеется ввиду то, что понимал Ландау, с той лишь разницей, что роль молекул в нашей схеме выполняют капли. Для каждого слоя составляется уравнение баланса числа капель. Смысл его состоит в том, что, если известно число капель в слоях в какой-то момент времени, то за малое приращение времени произойдет фиксируемое изменение числа капель в каждом из слоев в связи с поступлением в него капель, осаждающихся из вышележащего слоя и ухода капель по той же причине в нижележащий слой. Кроме того, на границе слоев, имеющих различную концентрацию капель, будут существовать диффузионные потоки. Поэтому в уравнение баланса войдут члены, описывающие изменение числа капель в слое за счет диффузионного обмена с соседними слоями. Шаг за шагом во времени или, что эквивалентно, по длине трубопровода, прослеживается изменение профиля концентрации по высоте трубы. По достижению определенного времени, соответствующей некоторой длине трубопровода, профиль перестает меняться. Устанавливается динамическое равновесие - на каждом уровне по высоте трубы число оседающих капель оказывается равным числу капель, выносимых диффузионными токами.
Что касается второго пункта этой методологии, то очевидно, что расслоение возникает тогда, когда объемная концентрация воды на нижнем уровне трубопровода достигает критического значения при отсутствии на глобулах бронирующих оболочек. Минимальная скорость потока, при которой это может произойти, и принимается за критическую скорость.
Результаты компьютерного моделирования движения девонской эмульсии по трубопроводу показали, что в начале трубопровода капли воды распределены равномерно, т.е. эмульсия однородна по сечению трубопровода.
Во всех случаях обводненность нефти изменялась в широких пределах. Первый вариант моделировал группу скважин, подключенных к общему трубопроводу. Расход жидкости при этом изменялся за счет числа работающих скважин или в связи с изменением дебитов некоторых из них. Второй вариант связан с решением задач предварительного сброса воды с помощью КДФ в местах, максимально приближенных к объектам закачки воды в продуктивные пласты.

где: и - средняя по расходу скорость потока; Re - число Рейнольдса потока.
За линейный масштаб принимается величина L = D/60
Скорость седиментации определяется по формуле Стокса (11)
где: - разность плотностей фаз; - динамическая вязкость сплошной фазы
Величины ni,32i, Wi характеризующие i-ю фракцию, находят следующим образом. Пусть
Р0 (х) есть плотность распределения объема дисперсной фазы по диаметрам частиц, т.е.
Р0 (x)dx -это объем, заключенный в частицах диаметром от х до х +dx. Тогда имеем (12):

где через Si0обозначена поверхность, приходящаяся на частицы i-й фракции. Оставшаяся величина рассчитывается из соотношения (7).
В качестве функции Р0(х) использовано распределение капель по размерам. Если воспользоваться безразмерными переменными R = x/0и Z =P00/W0, где0 - характерный размер частиц, a W0- объемная концентрация дисперсной фазы, то нормированная плотность распределения объема дисперсной фазы по размерам капель имеет вид (13):

где параметр распределения есть отношение саутеровского диаметра к максимальному диаметру капель (14):

Для равновесного распределения капель по размерам в трубопроводе, обусловленного процессами коалесценции и дробления, максимальный размер определяется из следующего эмпирического соотношения:
с-плотность сплошной фазы; - динамическая вязкость дисперсной фазы; - межфазное натяжение.
Оценка величины по промысловым данным позволила получить значение, равное 0,15.
Для дальнейших исследований была выбрана эмульсия со следующими характеристиками: плотность сплошной и дисперсной фаз равна соответственно 870 и 1150 кг/м3; динамические вязкости 0,015 и 0,00 мПас. Межфазное натяжение на границе раздела фаз было принято равным 0,010 н/м.
Алгоритм расчета был выбран итерационным. Расчет прекращался, когда условие (8) выполнялось с требуемой точностью. Значение W, в выражении (8) было принято равным 1,0.
Анализ результатов численных исследований показал, что расслоение потока происходит при определенном значении комплекса Q/D2, где Q - расход жидкости в трубе.
Поскольку этот комплекс, с точностью до постоянного коэффициента, есть не что иное, как скорость потока, то полученный результат означает, что переход эмульсионной структуры течения в расслоенную происходит при скорости потока, меньшей некоторой критической величины. Последняя существенно зависит от концентрации дисперсной фазы.
Характер зависимости показан на рис. 1. Особенно значительное изменение критической скорости наблюдается в области низких концентраций дисперсной фазы. Так, при изменении концентрации от 1 до 10 % значение критической скорости увеличивается с 0,34 до 0,51 м/с .
Здесь же, на рис. 1 представлены результаты расчета по методам работ [189, 200]. Напомним, что эти методы не учитывают полидисперсность эмульсии, а для определения критической скорости используют статическое условие в виде равенства скорости седиментации капель среднеквадратичной скорости турбулентных пульсаций.

Рис. 1. Зависимость критической скорости потока иоот концентрации дисперсной фазы W0 в
объемных единицах
Динамическая модель с учетом полидисперсности позволяет раскрыть влияние на переход от одной структуры потока к другой таких важных параметров, как концентрация дисперсной фазы и ее распределение по размерам капель.
Для выбора рационального диаметра трубопровода необходимо задать обводненность эмульсии и из рис. 1 найти значение критической скорости. Диаметр трубопровода рассчитывается из известного соотношения между расходом Q и скоростью течения:
Рассмотрим вопрос о размере капель, соответствующем переходу течения из эмульсионной структуры в расслоенное.
Пусть деэмульгатор не подается в систему сбора. В этом случае имеем стабильную эмульсию, и процессами коалесценции капель на линейных участках трубопроводов можно пренебречь. Расход жидкости считаем постоянным и равным 31,7 кг/с, варьируются только диаметр трубопровода и обводнённость. Полученные результаты представлены на рис. 2 в виде корреляционной связи между размером капель и диаметром трубопровода (см. рис. 2 а); размером капель и величиной обводненности эмульсии (см. рис. 2 б). Линии 2-4 и 6 на рис. 3а соответствуют значениям обводненности 40, 10, 1 и 0,1 объемных процента.
Линии 1-7 на рис. 3 б соответствуют значениям диаметра трубопровода 0,10; 0,15; 0,20; 0,25; 0,30; 0,35; 0,40.

Рис. 3 а. Корреляционная связь между диаметром трубопровода и глобул воды (Q = 31,7 кг/с)
Кривые 5, 3, 1 - зависимость максимального диаметра капель, способных витать в потоке, от диаметра трубопровода при обводненности эмульсии, равной 0,1; 1; 10 и 40%; кривая 4 - т о же, но в рамках старой теории; кривая 6 - зависимость максимального диаметра капель, устойчивых к дроблению, от диаметра трубопровода (по Слейчеру): кривая 7 - пересчет кривой 6 на саутеровский диаметр.

Рис. 3 б. Корреляционная связь между обводненностью эмульсии и диаметром глобул
Кривые 1-7 - для диаметра трубы, равного 0,10; 0,15; 0,20; 0,25; 0,30;0,35, 0,40 м.
Из рис. 3 следует, что в логарифмических переменных связи имеют линейный характер и справедлива формула (15)
где А, В, С-постоянные.
При А = -1 и В = -0,5 формула приводится к виду (16)

Для обводненности не выше 10% оценка константы С дала величину 31,2 ±1,5 мм2. При более высокой обводненности данные отклоняются от линейного закона (рис. 3 б ) и для 40% эмульсии С=26,0±1,0 мм2.
В случае, когда деэмульгатор подается в систему нефтегазосбора, на линейных участках трубопроводов бронирующие оболочки капель разрушаются и эмульсия становится нестабильной. В конце концов процессы коалесценции и дробления капель приводят к установлению динамического равновесия.
В этом случае задача состоит в определении наибольшего размера капель (саутеровского диаметра), при котором поток еще не будет расслаиваться. Процессы коалесценции и дробления учитываются с использованием уравнения (13).
Необходимо более подробно рассмотреть специфику принятой методологии оценки возможности расслоения потока в трубопроводах. Имеется достаточное число публикаций по этому вопросу, принципиально мало отличающихся друг от друга. Как правило, осуществляются лабораторные исследования, по которым в результате обработки получают формулы. Отдельные работы поднимаются до уровня определения критериальных чисел. Однако это мало что дает в практическом плане. Перенос таких лабораторных данных на промысловые условия не совсем корректен. В лучшем случае речь может идти о достижении частичного подобия лабораторных условий реальным промысловым. И практика подтверждает это: обилие различных формул, хорошо описывающих те опытные данные, на которых они были получены, мало пригодны за их пределами.
Рассмотрим методологию определения критической скорости, лежащей в основе большинства работ. Её можно изложить так: есть капля; под действием силы Архимеда она движется в окружающей среде (если легче, то всплывает; когда тяжелее среды – то оседает); скорость ее движения зависит от режима - для не очень крупных капель режим ламинарный и можно пользоваться известной формулой Стокса; кроме гравитационного движения капля участвует в пульсационном движении среды; капля не способна осесть и оказывается взвешенной в потоке, если среднеквадратичная скорость турбулентных пульсаций выше скорости ее осаждения; для определения критической скорости потока приравнивают указанные скорости. В конечном итоге получают связь между размером капель, способных витать в потоке, и скоростью потока.
Внешне методология логична. Тем не менее, она дает размеры капель, способных витать в потоке, намного превышающие реально наблюдаемые. Соответственно, она завышает значение критической скорости. скорости.
Более правилен другой подход к решению этой задачи по следующей схеме:
- эмульсия рассматривается не как «одиночная капля - окружающая среда», а как дисперсная система, причем не моно-, а поли-;
- замена статического условия равновесия динамическим;
- применение имитационного моделирования, рассчитывая на компьютере варианты развития системы во времени и пространстве.
В такой методологии первый пункт уже раскрыт на примере рассмотренной задачи укрупнения капель. Последний пункт реализуется по нижеследующей схеме: сечение трубопровода разделяется горизонтальными плоскостями от нижней образующей (дно трубы) до верхней на несколько слоев. Их число должно быть достаточно большим, но не настолько, чтобы нарушалось понятие физически малого (элементарного) объема. Под последним имеется ввиду то, что понимал Ландау, с той лишь разницей, что роль молекул в нашей схеме выполняют капли. Для каждого слоя составляется уравнение баланса числа капель. Смысл его состоит в том, что, если известно число капель в слоях в какой-то момент времени, то за малое приращение времени произойдет фиксируемое изменение числа капель в каждом из слоев в связи с поступлением в него капель, осаждающихся из вышележащего слоя и ухода капель по той же причине в нижележащий слой. Кроме того, на границе слоев, имеющих различную концентрацию капель, будут существовать диффузионные потоки. Поэтому в уравнение баланса войдут члены, описывающие изменение числа капель в слое за счет диффузионного обмена с соседними слоями. Шаг за шагом во времени или, что эквивалентно, по длине трубопровода, прослеживается изменение профиля концентрации по высоте трубы. По достижению определенного времени, соответствующей некоторой длине трубопровода, профиль перестает меняться. Устанавливается динамическое равновесие - на каждом уровне по высоте трубы число оседающих капель оказывается равным числу капель, выносимых диффузионными токами.
Что касается второго пункта этой методологии, то очевидно, что расслоение возникает тогда, когда объемная концентрация воды на нижнем уровне трубопровода достигает критического значения при отсутствии на глобулах бронирующих оболочек. Минимальная скорость потока, при которой это может произойти, и принимается за критическую скорость.
Результаты компьютерного моделирования движения девонской эмульсии по трубопроводу показали, что в начале трубопровода капли воды распределены равномерно, т.е. эмульсия однородна по сечению трубопровода.
Во всех случаях обводненность нефти изменялась в широких пределах. Первый вариант моделировал группу скважин, подключенных к общему трубопроводу. Расход жидкости при этом изменялся за счет числа работающих скважин или в связи с изменением дебитов некоторых из них. Второй вариант связан с решением задач предварительного сброса воды с помощью КДФ в местах, максимально приближенных к объектам закачки воды в продуктивные пласты.