2.017. Два точечных заряда q₁ = -50 нКл и q₂ = 100нКл находятся на расстоянии d =20 см друг от друга. Определить силу F, действующую q₃=-10нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.

Дано:

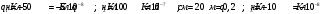
Найти:

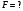
Решение:



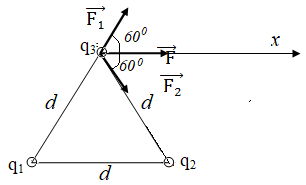
Точечные заряды находятся в вершинах равностороннего треугольника.

Согласно принципа суперпозиции:



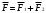
В проекциях на выбранную ось х:



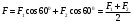
На основе закона Кулона:



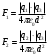
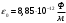- электрическая постоянная.

Получаем:



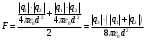
Подставляем числовые значения:



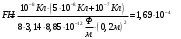
Ответ:

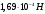
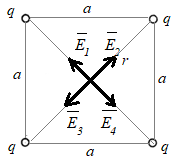
2.027. В вершинах квадрата со стороной а=10 см находятся заряды q₁ = q₂ = q₃ = q₄ = 10мкКл. Определить напряжённость Е и потенциал поля, создаваемого этими зарядами в центре квадрата.

Дано:

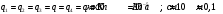
Найти:

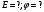
Решение:



Потенциал в центре квадрата равен алгебраической сумме потенциалов, создаваемых всеми зарядами в этой точке:



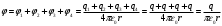
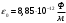- электрическая постоянная.

r - расстояние от центра квадрата до вершины



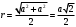
Получаем:



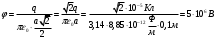
Напряженность поля в центре квадрата является векторной суммой напряженностей, создаваемых каждым зарядом в этой точке:

---

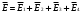
Модули этих напряженностей



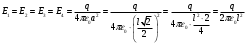
Удобно сначала сложить попарно векторы, направленные по одной диагонали (рис.): 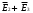 и 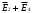 . При данных зарядах сумма 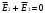, 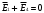. Поэтому результирующая напряженность: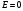


Ответ:
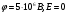
2.037. Шаровой слой, равномерно заряженный по объему с постоянной объемной плотностью ρ=1нКл/м³, имеет внутренний радиус R₁ = 3 см и внешний R₂ = 5см. Определить напряженность Е электрического поля в точках, отстоящих от центра шарового слоя на расстояниях r₁ = 2 см, r₂ = 4см и r₃ = 6см. Построить график зависимости напряженности Е от r.

Дано:



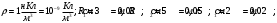
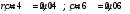
Найти:

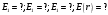
Решение:



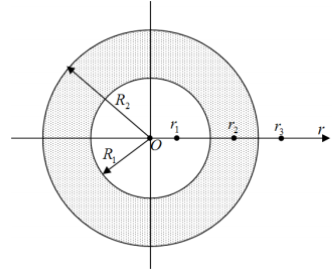
Так как заряд шара распределён в пространстве симметрично относительно центра шара О, то и электрическое поле симметрично относительно этой точки. Это позволяет применить для решения задачи метод Гаусса. Из симметрии задачи следует, что вектор 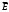направлен вдоль 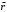и зависит только от расстояния до центра шара r. Выберем гауссову поверхность в виде сферы, переменного радиуса r с центром в точке О. Учтем, что модуль напряжённости поля шара одинаков во всех точках этой поверхности и 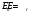. Так как шар диэлектрический, следует применить теорему Гаусса для вектора электрического смешения D. Тогда поток вектора смешения сквозь гауссову поверхность: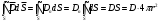



Где S - площадь гауссовой поверхности, r - сё радиус.

---

Всё пространство можно разбить на 3 области:

1. 
   ая: 01 < R₁,
   
2. 
   ая: R₁< r₂ < R₂.
   
3. 
   ья: r₃> R₂.
   

Применим теорему Гаусса для каждой области.

Для области : 0<r₁ < R₁.

Величина свободного заряда, охватываемого поверхностью интегрирования в пределах первой области, равна нулю. Следовательно, поток вектора смешения также равен нулю, а так как площадь поверхности не нулевая, то смещение и напряжённость поля в пределах первой области равны нулю:



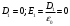
- электрическая постоянная.

Для области R₁< r₂ < R₂.



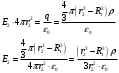
Подставляем числовые значения:



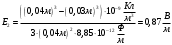
Для области r₃> R₂



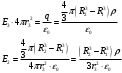
Подставляем числовые значения:



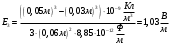
Запишем функцию зависимости напряженности Е от r:



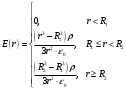
Cтроим график зависимости напряженности Е от r :


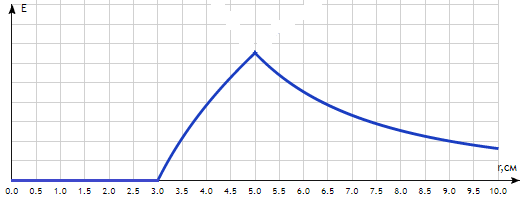
Ответ:

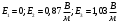
2047. Электрическое поле создано двумя одинаковыми положительными зарядами q_l и q₂. Определить работу А сил поля по перемещению заряда q = 10 нКл из точки 1 с потенциалом φ₁ =300 В в точку 2.

Дано:

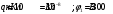
Найти:

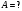
Решение:



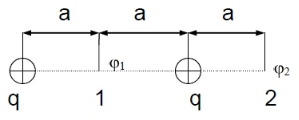
Работа сил электростатического поля по перемещению заряда из точки с потенциалом в точку с потенциалом равна:



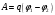
Согласно принципу суперпозиции потенциалы поля в точках 1 и 2 складываются из потенциалов полей

---

, связанных зарядами А и В, то есть:



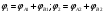
Потенциал поля точечного заряда q:



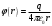
Тогда:



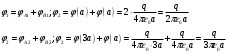
Выразим неизвестный заряд через φ₁ и подставим φ₂:



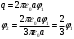
Тогда:


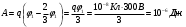
Ответ:
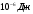
2.057. Плоский конденсатор заполнен диэлектрикам и на его пластины подана некоторая разность потенциалов. Энергия конденсатора в этом случае равна W = 20мкДж. После того, как конденсатор отключили от источника напряжения, диэлектрик вынули из конденсатора. Работа, которую надо было совершить против сил электрического поля, чтобы вынуть диэлектрик, А=70мкДж. Определить диэлектрическую проницаемость ε диэлектрика.

Дано:

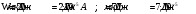
Найти: 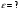ε - ?

Решение:

Емкость плоского конденсатора

А) с диэлектриком:

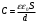
Б) без диэлектрика:

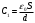
Энергия заряженного конденсатора



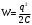
После того как вынули диэлектрик емкость конденсатора уменьшилась в ε раз, заряд остался прежним, а энергия приняла значение



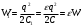
Изменение энергии равно работе внешних сил


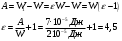
Ответ: 4,5


2.067. К батарее аккумуляторов, ЭДС которой равна 2В и внутреннее сопротивление r=0,5Ом, присоединен проводник. Определить: 1) сопротивление R проводника, при котором мощность, выделяемая в нем, максимальна; 2) мощность Р, которая при этом выделяется в проводнике

Дано: ε = 2 В; r = 0,5 Ом

Найти: R = ?; P_max

---

= ?

Решение:



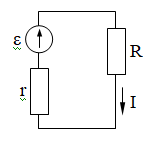
Сила тока в цепи

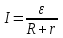
Мощность, выделяющаяся в проводнике:



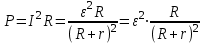
Исследуем функцию P(R) на экстремум:





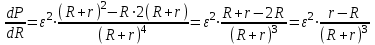
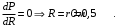
При таком сопротивлении проводов мощность, выделяющаяся в проводах, будет максимальной.




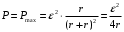
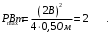
Ответ:


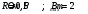
2.077. ЭДС батареи ε =120 В, сопротивления R₃ =20Ом и R₄ =25 Ом. Падение напряжения на сопротивлении R₁ равно U₁ =40B. Амперметр показывает ток I =2А. Определить сопротивление R₂

Дано:

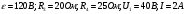
Найти:

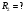
Решение:



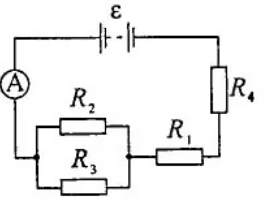
Падение напряжения на параллельно соединенных сопротивлениях:

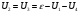(1)

Учитывая, что



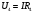
уравнение (1) запишется:



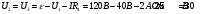
Сумма токов, протекающих через сопротивления R₂ и R₃ равна току, который показывает амперметр:



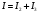
Согласно закона Ома:



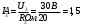
Тогда



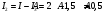
Согласно закона Ома:



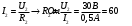
Ответ: 60Ом

---

Смотрите также файлы

• Масленица в гости к нам пришла.docx

• .docx

• Внезапная головная больнарушение координациинарушение зрения.pdf

• Если гражданин нашел работу за пределами территории Российской Федерации и заключил с иностранным работодателем договор (контракт), он подчиняется требованиям трудового законодательства страны работодателя.docx

• Тема курсовой работы Расчет экономической эффективности от закачки горячей нефти Камасев Д. А.pptx