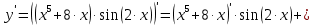Файл: Решение с помощью формул Крамера 2 записать систему в матричной форме и решить ее средствами матричного исчисления.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 18
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задания №_5. Дана система линейных уравнений с тремя неизвестными. Требуется: 1) найти ее решение с помощью формул Крамера; 2) записать систему в матричной форме и решить ее средствами матричного исчисления.
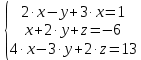
Решение:
1) найти ее решение с помощью формул Крамера;
запишем определитель системы:
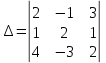
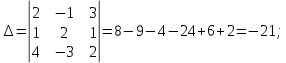
Заменим в
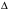 столбец коэффициентов при
столбец коэффициентов при  на столбец правых частей
на столбец правых частей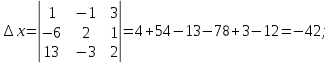
Заменим в
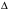 столбец коэффициентов при
столбец коэффициентов при 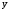 на столбец правых частей
на столбец правых частей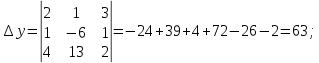
Заменим в
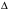 столбец коэффициентов при
столбец коэффициентов при  на столбец правых частей
на столбец правых частей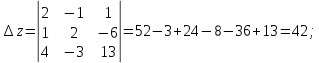
По формулам Крамера получаем решение :
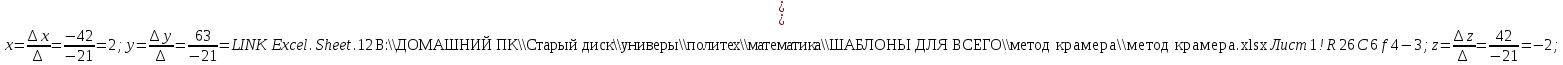
2) записать систему в матричной форме и решить ее средствами матричного исчисления
Пусть
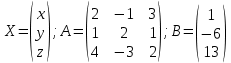 . Тогда данную систему можно записать в виде матричного уравнения . Решаем его, домножая слева на обратную матрицу:
. Тогда данную систему можно записать в виде матричного уравнения . Решаем его, домножая слева на обратную матрицу: 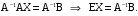 Отсюда получаем решение
Отсюда получаем решение 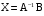 . Найдем сначала
. Найдем сначала 
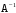 .
.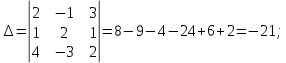
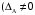 ,значит
,значит 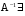 ).
).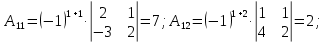
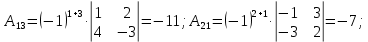
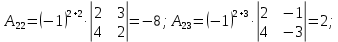
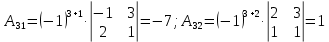
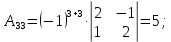
Составляем обратную матрицу
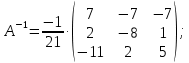
Найдем:
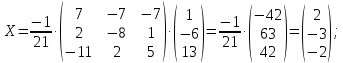
Ответ: х= 2; у= -3; z= -2.
Задания №_35. Даны координаты вершин треугольника АВС. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) угол В в радианах с точностью до двух знаков; 4)уравнение высоты CD и ее длину; 5) уравнение медианы АМ и ко-ординаты точки К пересечения этой медианы с высотой CD.
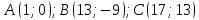
Решение:
1) длину стороны АВ:
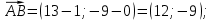
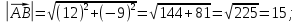
2) уравнения сторон АВ и ВС и их угловые коэффициенты:
АВ:
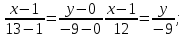
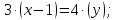
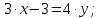
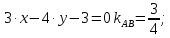
ВC:
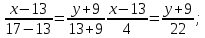
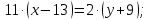
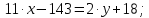
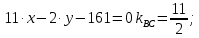
3) угол
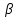 в радианах с точностью до двух знаков:
в радианах с точностью до двух знаков: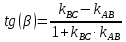
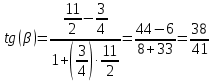
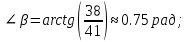
4)уравнение высоты CD и ее длину:
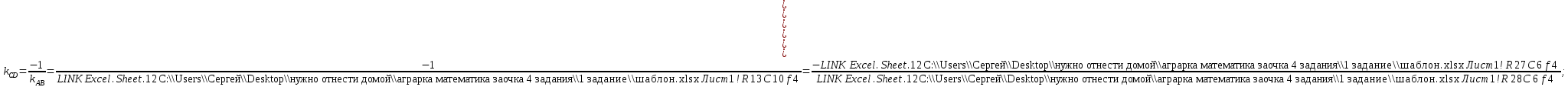
Уравнение прямой, проходящей через данную точку M1 (x
1 ; y1 ) в заданном угловым коэффициентом k направлении, имеет вид:
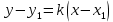
Подставив координаты точки С и
 , получим уравнение высоты CD:
, получим уравнение высоты CD:
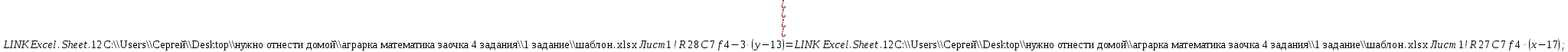
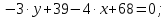
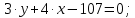
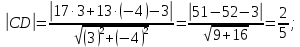
5) уравнение медианы АМ и координаты точки К пересечения этой медианы с высотой CD.
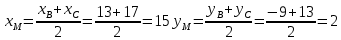
АМ:
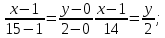
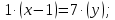
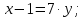
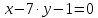
точка К:
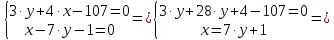
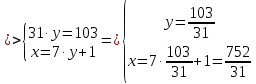
Задания №_55. Даны координаты вершин пирамиды ABCD.
Н
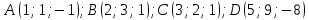
Решение:
-
координаты векторов AB , AС , AD и их длины:
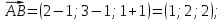
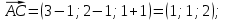
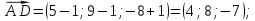
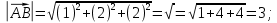
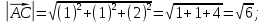
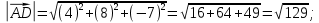
-
угол между ребрами AB и AD:
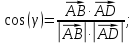
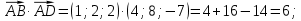
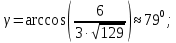
-
площадь грани ABC;
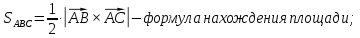
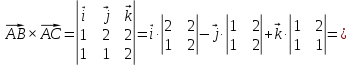
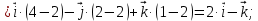
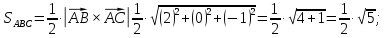
-
объем пирамиды;
Vпир.=
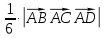 ;
;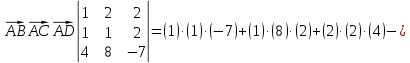
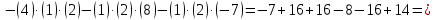
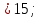
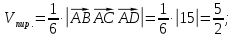
5)уравнение прямой AB:
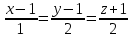
-
уравнение плоскости ABC:
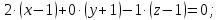
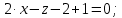
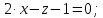
-
уравнение высоты, опущенной из вершины D на грань ABC.
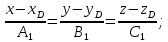
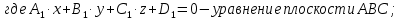
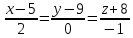
Задания №_65. Найти указанные пределы.
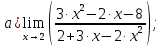
Решение:
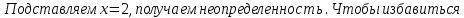
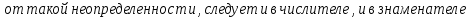
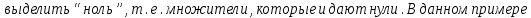
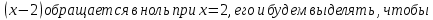
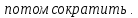
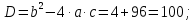
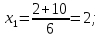
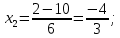
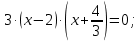
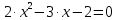
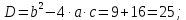
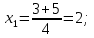
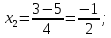
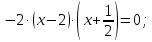
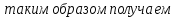 :
: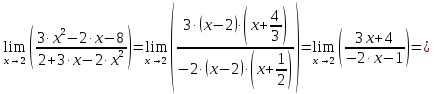
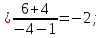
Ответ:
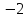 .
.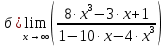
Решение:
При подстановке
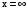 получаем неопределенность
получаем неопределенность  . Чтобы избавиться
. Чтобы избавиться от такой неопределенности, следует и в числителе, и в знаменателе вынести за скобки наивысшую степень x.
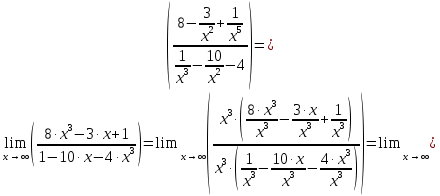
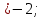
Ответ:
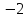 .
.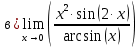
Решение:
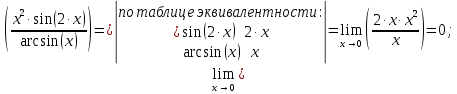
Ответ:
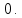
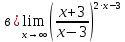
Решение:
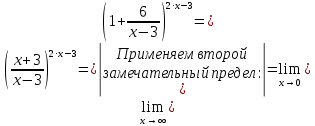
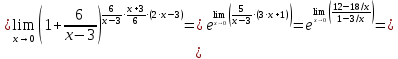
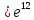
Ответ:
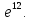
Задания №_75. Найти производные данных функций.
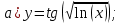
Решение:
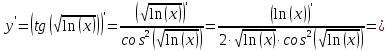
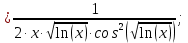
Ответ:
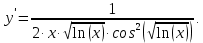
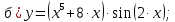
Решение: