ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 21
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое задание 6
Тема 1.11. Критерии проверки гипотез
Формулировка задания
А) Проверить параметрическую гипотезу о том, что заданное значение m0 является математическим ожиданием нормально распределенной случайной величины при 5-процентном уровне значимости для двусторонней критической области, если в результате обработки выборки объема n = 10 получено выборочное среднее
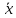 , а выборочное среднее квадратичное отклонение равно S1.
, а выборочное среднее квадратичное отклонение равно S1.Б) При уровне значимости α = 0,1 проверить статистическую гипотезу о равенстве дисперсий двух нормально распределенных случайных величин Х и Y на основе выборочных данных при альтернативной гипотезе:
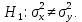
Таблица 6.1
| № вар. | а | б | |||||||
| m0 | 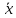 | S1 | X | Y | |||||
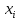 | 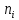 | 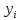 | 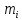 | ||||||
| 1 | 10 | 12 | 1 | 142 145 146 148 | 3 1 2 4 | 140 146 147 151 | 5 3 2 2 | ||
| 2 | 20 | 22 | 4 | 37 38 40 41 42 | 2 1 4 3 6 | 38 39 40 41 43 | 4 3 2 2 3 | ||
| 3 | 20 | 18 | 2 | 39 43 45 47 51 | 4 2 3 4 2 | 75 80 84 91 94 | 4 2 3 4 2 | ||
| 4 | 40 | 44 | 3 | 9 10 11 12 14 | 4 5 3 2 1 | 9 10 11 13 14 | 5 6 4 8 3 | ||
| 5 | 58 | 56 | 4 | 20 22 23 24 26 | 3 4 2 2 4 | 18 19 20 22 23 | 6 3 4 2 5 | ||
| 6 | 60 | 64 | 6 | 31 33 34 38 42 | 6 2 1 3 2 | 85 88 95 97 100 | 1 3 4 2 5 | ||
| 7 | 70 | 66 | 8 | 15 17 20 21 25 | 1 3 2 4 6 | 20 22 23 25 26 | 4 2 2 3 1 | ||
| 8 | 70 | 72 | 5 | 27 29 32 33 34 | 3 9 6 2 1 | 28 29 30 32 34 | 8 9 4 9 2 | ||
| 9 | 50 | 48 | 2 | 16 18 21 24 25 | 12 10 14 8 6 | 18 25 29 36 40 | 3 1 4 6 6 | ||
| 10 | 30 | 34 | 4 | 71 73 75 79 80 | 4 5 8 10 3 | 68 69 70 74 78 | 10 14 13 12 11 | ||
Рекомендации по выполнению задания
Номер варианта задания Вы можете определить, используя табл. 6.2, по первой букве Вашей фамилии. Необходимо решение расписывать как можно подробнее, обязательно описывать формулы, которыми пользуетесь во время решения. Кроме того, обязательно должны быть записаны условие задания, ответ.
Таблица 6.2
Выбор варианта задания
| Буква | А, Ф, Э | Б, М, Х | В, Ю | Г, У,Я | Д, Ч, С | Е, Н, П | Ж, О, З | И, Ц | К, Т, Ш, Щ | Л, Р |
| № вар. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Образец выполнения задания
Задание
А) Проверить параметрическую гипотезу о том, что заданное значение m0 является математическим ожиданием нормально распределенной случайной величины при 5-процентном уровне значимости для двусторонней критической области, если в результате обработки выборки объема n = 10 получено выборочное среднее
 , а выборочное среднее квадратичное отклонение равно S1.
, а выборочное среднее квадратичное отклонение равно S1.Б) При уровне значимости α = 0,1 проверить статистическую гипотезу о равенстве дисперсий двух нормально распределенных случайных величин Х и Y на основе выборочных данных при альтернативной гипотезе:

Решение
Для проверки статистической гипотезы необходимо выбрать статистику и по этой формуле вычислить ее выборочное значение, затем полученное число сравнить с критическим значением данной статистики в зависимости от вида альтернативной гипотезы. В табл. 6.3 приведены статистики и условия принятия гипотез для основных параметрических гипотез.
Таблица 6.3
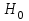 | Предположе-ния | Статистика критерия | 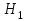 | Область принятия 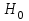 |
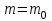 | 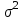 известно | 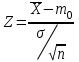  | 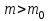 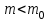 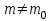 | 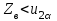 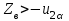 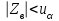 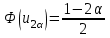 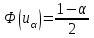 |
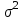 неизвестно | 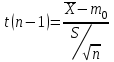 | 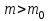 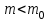 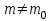 | 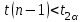 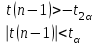 | |
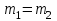 |  и и  известно | 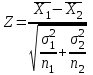 | 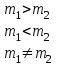 | 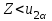 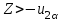 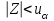 |
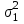 и и 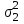 Неизвестно Причем 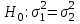 принимается принимается | 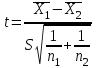 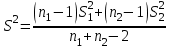 | 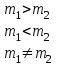 | 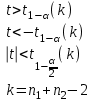 | |
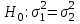 отклоняется | 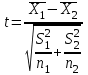 | 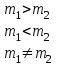 | 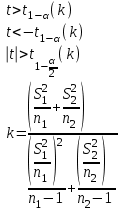 | |
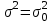 | 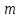 известна | 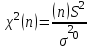 | 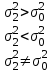 | 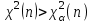 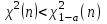 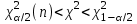 |
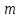 неизвестна | 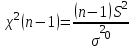 | 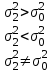 | 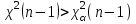 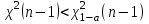 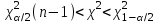 | |
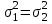 | 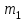 и и 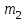 известны | 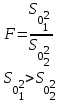 | 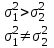 | 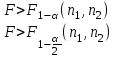 |
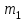 и и 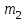 неизвестны | 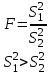 | 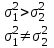 | 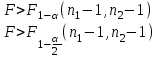 |
А) Проверяемая гипотеза H0: m= m0, при альтернативной гипотезе H1: m ≠ m0.
H0: m= 50,
H1: m≠ 50.
Так как σ неизвестна, то наша ситуация соответствует второй строке табл. 6.3, и выбираем статистику
 .
.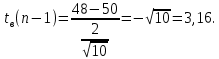
По таблице критических точек распределения Стьюдента
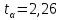 (степень свободы n – 1). Так как
(степень свободы n – 1). Так как 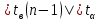 , то гипотеза H0 отклоняется и принимается гипотеза H1, т. е. математическое ожидание случайной величины не равно 50.
, то гипотеза H0 отклоняется и принимается гипотеза H1, т. е. математическое ожидание случайной величины не равно 50.Б)
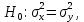

Так как математическое ожидание неизвестно, то выбираем последнюю строку в табл. 6.3.
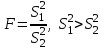 , т. е. первой будет та выборка, у которой выборочная дисперсия больше.
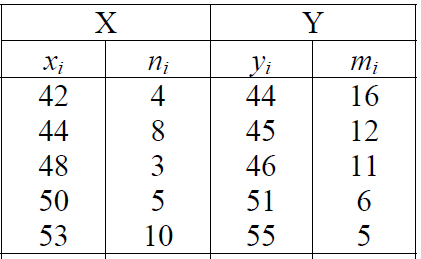
, т. е. первой будет та выборка, у которой выборочная дисперсия больше. Вычислим среднее арифметическое и выборочную дисперсию.
| xi | ni | 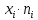 | 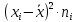 |
| 42 | 4 | 168 | 150,4711 |
| 44 | 8 | 352 | 136,6756 |
| 48 | 3 | 144 | 0,053333 |
| 50 | 5 | 250 | 17,42222 |
| 53 | 10 | 530 | 236,8444 |
| Сумма | 30 | 1444 | 541,4667 |
| |  = = | 48,13333, | |
| | 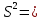 | 18,04889. | |
| yi | ni | 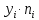 | 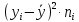 |
| 44 | 16 | 704 | 109,8304 |
| 45 | 12 | 540 | 31,4928 |
| 46 | 11 | 506 | 4,2284 |
| 51 | 6 | 306 | 115,1064 |
| 55 | 5 | 275 | 351,122 |
| Сумма | 50 | 2331 | 611,78 |
| | 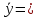 | 46,62, | |
| |  | 12,2356. | |
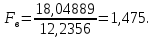 Критическое значение определяется по таблице распределения Фишера по уровню значимости α = 0,1 и степеням свободы
Критическое значение определяется по таблице распределения Фишера по уровню значимости α = 0,1 и степеням свободы 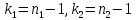 .
.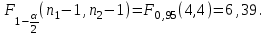
Так как 1,475 < 6,39, то нулевая гипотеза отклоняется и дисперсии выборок различны.