Автономная некоммерческая организация высшего образования

«МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра Экономики и управления

Форма обучения: Дистанционная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

Математика

Группа

Студент





МОСКВА 2023

Практические задания Задачи:
1. Выполнить деление комплексных чисел

1.1 i

????

1.2

????
2. Вычислить пределы последовательностей

2.1.

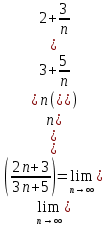
2 .2. =


????
=

.

.
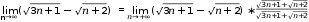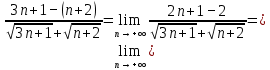
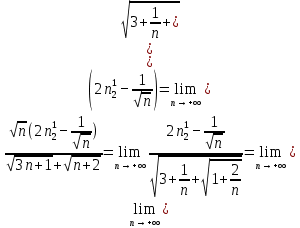
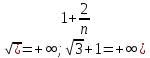
3. Используя признаки Даламбера и Коши исследовать сходимость рядов

3.1.



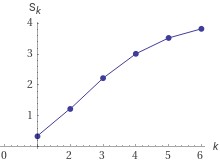
Применим сравнительный признак: α=-3.

Поскольку α меньше 1, то ряд расходится.

3.2.



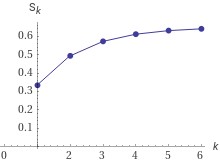
Применим радикальный признак Коши

---

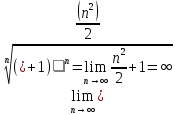
Поскольку полученное значение равно 1, то получаем неопределенность.

Признак Даламбера. , при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования).

.

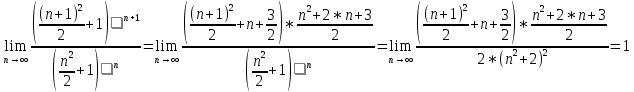
Поскольку q = 1, то получаем неопределенность.

Рассмотрим предел исходного ряда.

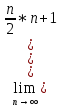
Данный предел не равен 0. Необходимое условие сходимости не выполняется, следовательно, ряд расходится.

4. 
   Найти производные сложных функций
   

4.1. y = sin (ln x) = (ln(sinx)) = 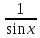* *cosx=ctgx

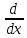4.2. = In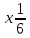 = 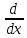In g * = =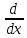
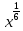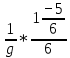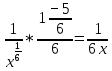
5. Вычислить неопределенный интеграл

5.1. ∫ ????³ sin 2???? ???? ????

.

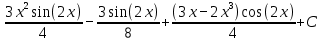
5.2. ∫ ????² 2^???? ???? ????

.
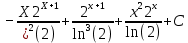
6. Найти частные производные первого и второго порядка

6.2.



7 Найти сумму матриц

7.1 A+B =

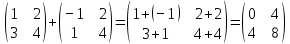
7.2 A+B =
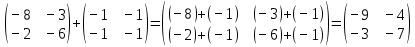
8. Найти произведение матриц

8.1. A * B =

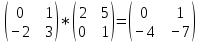
C11=0*2+1*0=0

C12=0*5+1*(-1)=-1

C21=(-2)*2+3*0=-4

C22=(-2)*5=3*(-1)=-13

---

8.2. A * B =

C11=6 · 0 + 2 · 5 = 0 + 10 = 10

C12= 6 · (-6) + 2 · 7 = (-36) + 14 = -22

C21=3 · 0 + 8 · 5 = 0 + 40 = 40 C22=3 · (-6) + 8 · 7 = (-18) + 56 = 38
9. Найти определители матриц

9.1. A =

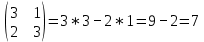
9.2. A =



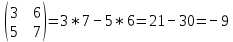
10.1
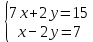
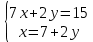
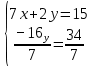
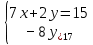
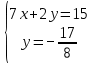
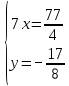
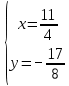
10.2

.

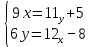
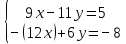
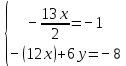
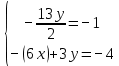
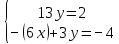
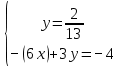
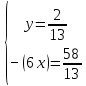
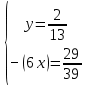
11. Для заданных векторов найти смешанное произведение [ ⃗????⃗ × ????⃗ ] ∙ ⃗????

11.1. ???? = (1; -2; 1) ????⃗ = (2; 1; -2) ???? = (1; 1; 1)

1·1·1 + (-2)·(-2)·1 + 1·2·1 - 1·1·1 - (-2)·2·1 - 1·(-2)·1 = 1 + 4 + 2 - 1 + 4 + 2 = 12

11.2. ???? = (1; 1; 2) ????⃗ = (1; -1; 3) ???? = (-2; -2; 2)

1·(-1)·2 + 1·3·(-2) + 2·1·(-2) - 2·(-1)·(-2) - 1·1·2 - 1·3·(-2) = -2 - 6 - 4 - 4 - 2 + 6 = -12

---

Смотрите также файлы

• Урок по истории России 11 класс. Учитель Агалакова Е. В. План урока.ppt

• Строгание древесины.docx

• Вебсайт часто делится на заголовки, меню, содержание и нижний колонтитул.docx

• Черная смерть.docx

• Глобализация. Глобальные проблемы современности. Цель урока.ppt