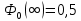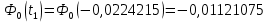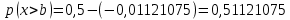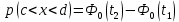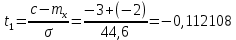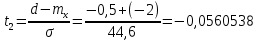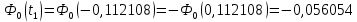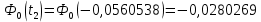ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 38
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание №3
Стационарный случайный процесс x(t) имеет одномерную функцию плотности вероятности (ФПВ) мгновенных значений W(x), график и параметры которой приведены в таблице 4.
Требуется:
1. Определить параметр h ФПВ.
2. Построить ФПВ W(x) и функцию распределения вероятностей (ФРВ) F(x) случайного процесса.
3. Определить первый m1 (математическое ожидание) и второй m2 начальные моменты, а также дисперсию D(x) случайного процесса.
| M | ФПВ W(x) | N | Параметры ФПВ | ||||
| 5 | 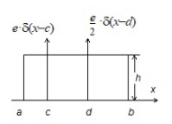 | | a | b | c | d | e |
| 6 | 3 | 10 | 5 | 7 | 0,1 | ||
Рисунок 3.1 Вид заданной функции плотности вероятности
Решение:
-
Аналитическая запись данной ФПВ имеет вид:
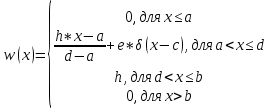(1.1)Параметр h ФПВ можно вычислить из условия нормировки:
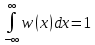(1.2)Подставив значения из (1.1) в формулу (1.2) получим:
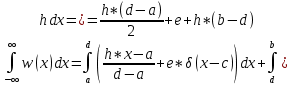
Подставим значения своего варианта посчитаемh
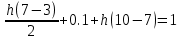
Из этого следует
-
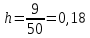
ФРВ связана с ФПС данным соотношением:
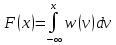(1.3)при -∞
Исходя из формул (1.1) и (1.3) можно вычислить значения функций w(x) и F(x) для отдельных участков.
Для x ≤ a = 3
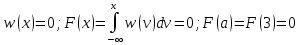
Для a < x ≤ d => 3 < x ≤ 7
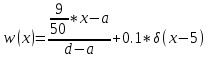
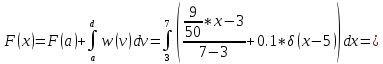
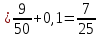(1.4)Значение вероятности в единичном скачке:
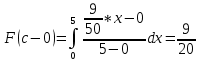
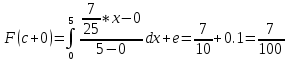
Для d < x ≤ b => 7 < x ≤ 10
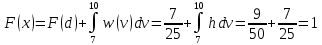
Для x > b = 10:
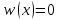
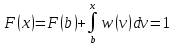
Графики ФПВ и ФРВ:
W(x)
0,3
0,2
0,1
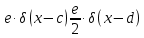
3 5 7 10 x
Рисунок 1.2 Функции плотности вероятности
F(x)
1
5/6
4/6
3/6
2/6
1/6
0 1 2 3 4 5 6 7 8 9 10 х
Рисунок 1.3 Функцию распределения вероятностей
-
Определим первый начальный момент m1 (математическое ожидание)
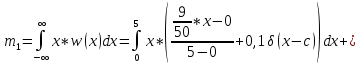
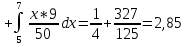
Вычисляем m2 второй начальный момент:
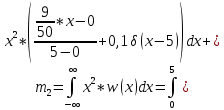
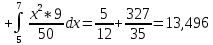
Найдем дисперсию случайного процесса:
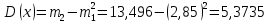
Задача №4
Энергетический спектр гауссовского стационарного случайного процесса x(t) равен G(). Среднее значение случайного процесса равно mx = m1= M{x(t)}.
Требуется :
1. Определить корреляционную функцию B() случайного процесса.
2. Рассчитать величины эффективной ширины спектра и интервала корреляции рассматриваемого процесса.
3. Изобразите графики G() и B() с указанием масштаба по осям и покажите на них эффективную ширину спектра и интервал корреляции.
4. Запишите выражение для функции плотности вероятности W(x) гауссовского стационарного случайного процесса и постройте её график.
5. Определите вероятности того, что мгновенные значения случайного процесса будут меньше ap(x<a); будут больше bp(x>b); будут находиться внутри интервала [c,d] p(c<x<d).
Исходные данные к задаче представлены в таблицах 4.1 и 4.2.
Таблица 4.1 Исходные данные
| Предпоследняя цифра номера студенческого билета | Функция энергетического спектра,  |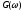
| 5 | G00при 0, G() = 0при 0. |
Таблица 4.2 Исходные данные
| Последняя цифра номера студенческого билета | 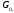 ,  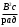|  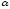 ,  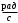| 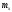 | a | b | c | d |
| 6 | 50 | 250 | -2 | -4 | 1 | -3 | -0,5 |
1.
Для нахождения корреляционной функции B() воспользуемся формулой Винера-Хинчина:
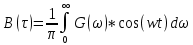
Интеграл будем брать в пределах от 0 до ∞, и заменим 0на Ω
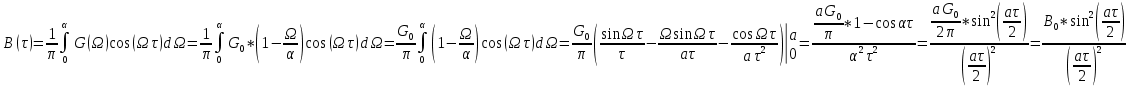
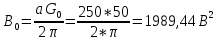
2.
Рассчитаем величину эффективной ширины спектра
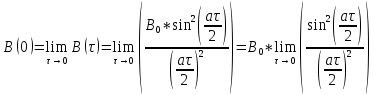
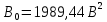
Определим эффективную ширину спектра случайного процесса:
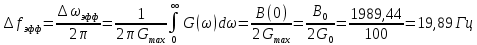
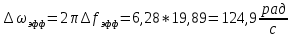
Найдем интервал корреляции данного процесса:
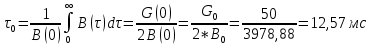
3
Графики G() и B()
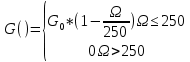
Для удобства брались значения Ω = k*a, где k = 0;0,1;0,2…1
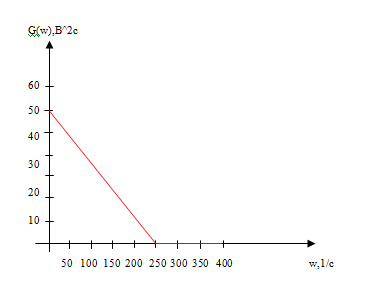
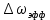
Рисунок 4.1 График функции G()
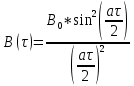
Для удобства брались значения w = k/a, где k = -20,-15,-10,-5,0,5,10,15
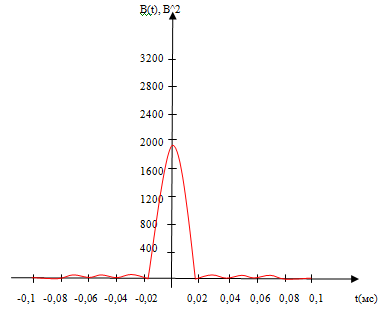
Рисунок 4.2 График функции B(t)
4
Найдем дисперсию случайного процесса
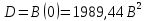
Найдем значение плотности вероятности w(x) для данного гауссовскогостационарного случайного процесса:
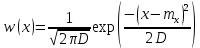
Подставим значения по варианту и простроим график полученной функции
.
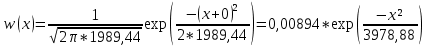
x
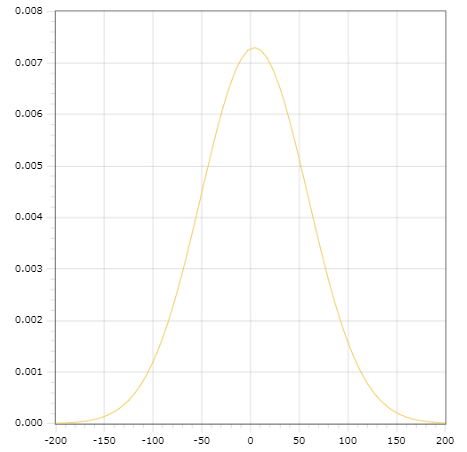
x
Рисунок 4.3 График W(x)
5
Определите вероятности того, что мгновенные значения случайного процесса будут меньше a - p(x<a); будут больше b - p(x>b); будут находиться внутри интервала [c,d] - p(c<x<d).
Выразим интервальную вероятность
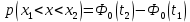
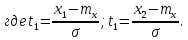
Среднее квадратичное отклонение будет равно
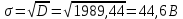
Интеграл вероятности определяется выражением
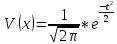
Функция ошибок Ф0(t) табуирована и имеет вид:
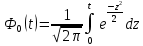
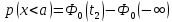
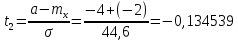
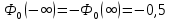
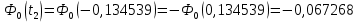
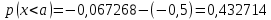
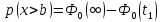
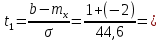-0,0224215
