Файл: Контрольная работа 1 Задача 1 Даны векторы и. Найти вектор, модуль вектора, скалярное произведение, где.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 20
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Контрольная работа №1
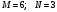
Задача 1
Даны векторы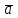 
и 
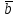. Найти вектор 
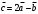, модуль вектора 
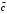, скалярное произведение 
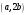, где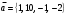 
, 
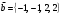
Решение
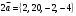
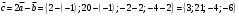
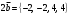
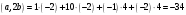
Задача 2
Даны матрица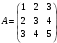 
и вектор-строка 
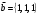. Найти произведения 
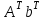и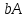 
.
Решение
Транспортирование матрицы – переход от матрицы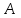 
к матрице 
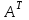, в которой строки и столбцы поменялись местами с сохранением порядка:
; 
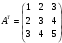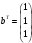
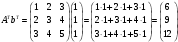
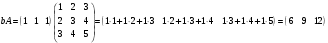
Задача 3
Даны матрицы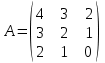 
и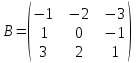 
. Проверить, коммутативны ли матрицы 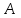и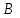 
, и найти определители матриц.
Решение
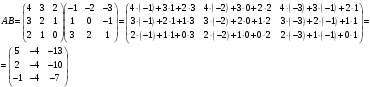
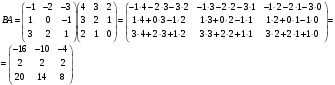
Так как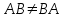 
, то матрицы и не являются коммутативными.
Воспользуемся формулой для вычисления определителя матрицы по первой строке:
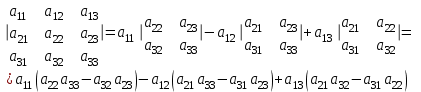
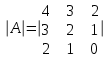
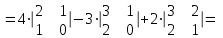
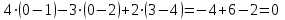
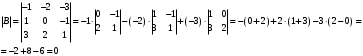
Задача 4
Решить систему из трех уравнений, пользуясь формулой Крамера и методом Гаусса:
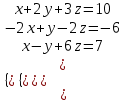
1) метод Крамера
Обозначим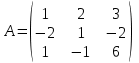 
, 
, 
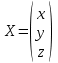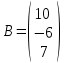
Найдем определитель системы
∆ 
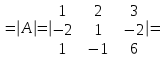
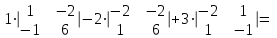
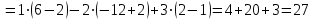
Так как ∆ 
0, то по теореме Крамера система имеет единственное решение.
Вычислим определители матриц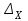 
, 
, 
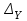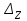, полученных из матрицы А заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:
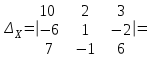
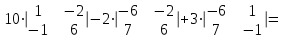
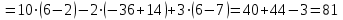
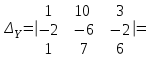
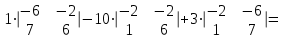
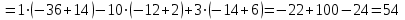
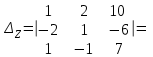
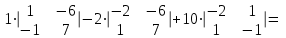
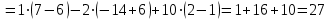
Теперь по формулам Крамера
; 
; 
,
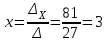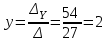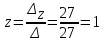т.е. решение системы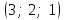 
2) метод Гаусса
Расширенная матрица системы имеет вид:
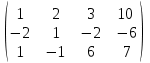
Умножая первую строку на 2 и прибавляя полученную строку ко второй, исключим переменную х1 из второй строки:
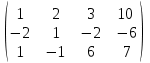
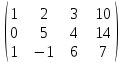
Умножая первую строку на (-1) и прибавляя полученную строку к третьей, исключим переменную х1 из третьей строки:
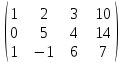
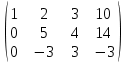
Так как теперь а22 ≠ 0, то умножая вторую строку на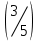 
и прибавляя полученную строку к третьей, исключим переменную х2 из третьей строки:
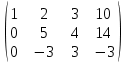
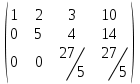
Получим систему уравнений
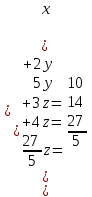
откуда, используя обратный ход метода Гаусса, найдем из третьего уравнения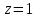 
; из второго уравнения 
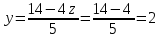и из первого уравнения 
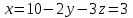, т.е. решение системы (3; 2; 1)
Задача 5
Найти ранг матрицы 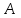размерностью 4×4. Найти определитель матрицы:
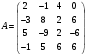
Шаг 1
Так как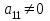 
, то умножая первую строку матрицы соответственно на числа 1,5, -2,5, 0,5, и прибавим полученные строки соответственно ко второй и третьей строкам
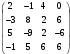
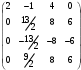
Шаг 2
Так как теперь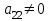 
, то умножая вторую строку матрицы на числа 1, 
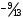, и прибавим полученные строки соответственно к третьей и четвертой строкам
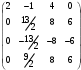
Контрольная работа №1
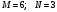
Задача 1
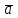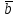Даны векторы и . Найти вектор 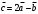, модуль вектора 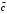, скалярное произведени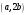е , где ,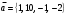
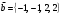
Решение
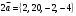
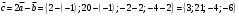
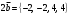
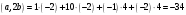
Задача 2
Даны матрица 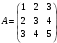и вектор-строка 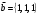. Найти произведения 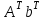и .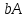
Решение
Транспортирование матрицы – переход от матрицы 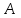к матрице 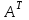, в которой строки и столбцы поменялись местами с сохранением порядка:
;
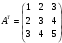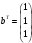
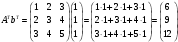
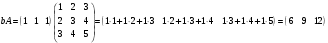
Задача 3
Даны матрицы 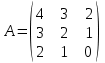и 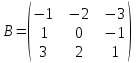. Проверить, коммутативны ли матрицы 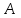и 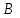, и найти определители матриц.
Решение
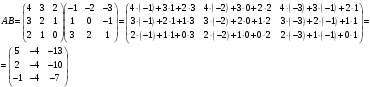
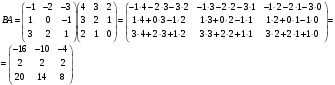
Так как 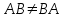, то матрицы 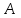и 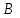не являются коммутативными.
Воспользуемся формулой для вычисления определителя матрицы по первой строке:
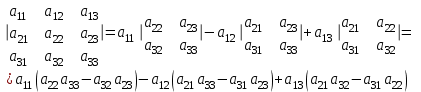
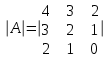
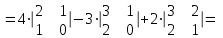
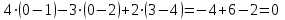
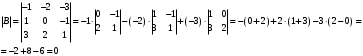
Задача 4
Решить систему из трех уравнений, пользуясь формулой Крамера и методом Гаусса:
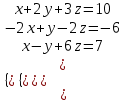
1) метод Крамера
Обозначим , ,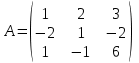
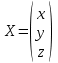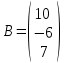
Найдем определитель системы
∆
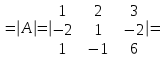
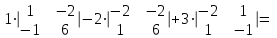
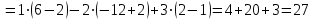
Так как ∆ 0, то по теореме Крамера система имеет единственное решение.
Вычислим определители матриц 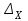, , 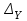, 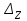полученных из матрицы А заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:
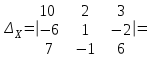
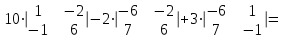
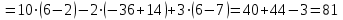
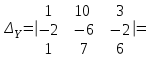
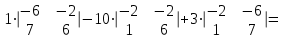
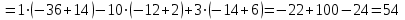
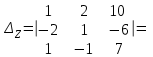
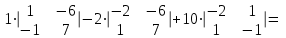
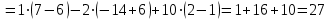
Теперь по формулам Крамера
; ; ,
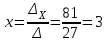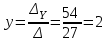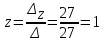т.е. решение системы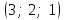
2) метод Гаусса
Расширенная матрица системы имеет вид:
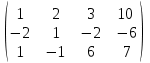
Умножая первую строку на 2 и прибавляя полученную строку ко второй, исключим переменную х1 из второй строки:
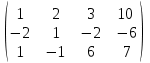
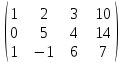
Умножая первую строку на (-1) и прибавляя полученную строку к третьей, исключим переменную х1 из третьей строки:
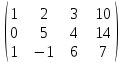
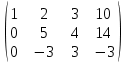
Так как теперь а22 ≠ 0, то умножая вторую строку на 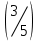и прибавляя полученную строку к третьей, исключим переменную х2 из третьей строки:
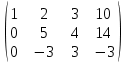
Контрольная работа №1
Задача 1
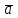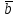Даны векторы и . Найти вектор 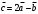, модуль вектора 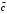, скалярное произведени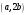е , где ,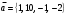
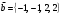
Решение
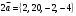
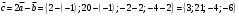
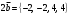
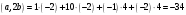
Задача 2
Даны матрица 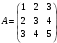и вектор-строка 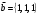. Найти произведения 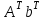и .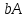
Решение
Транспортирование матрицы – переход от матрицы 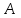к матрице 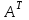, в которой строки и столбцы поменялись местами с сохранением порядка:
;
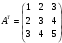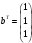
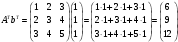
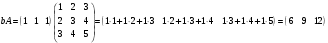
Задача 3
Даны матрицы 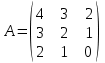и 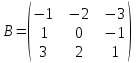. Проверить, коммутативны ли матрицы 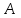и 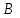, и найти определители матриц.
Решение
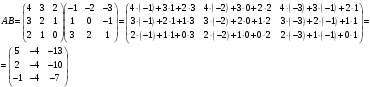
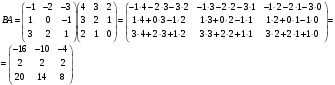
Так как 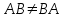, то матрицы 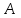и 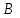не являются коммутативными.
Воспользуемся формулой для вычисления определителя матрицы по первой строке:
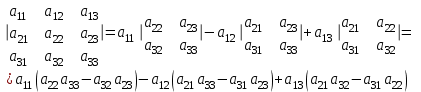
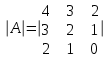
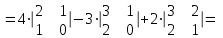
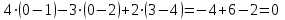
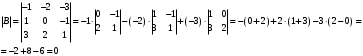
Задача 4
Решить систему из трех уравнений, пользуясь формулой Крамера и методом Гаусса:
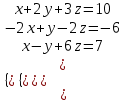
1) метод Крамера
Обозначим , ,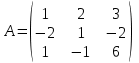
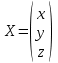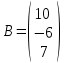
Найдем определитель системы
∆
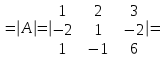
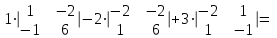
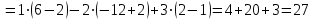
Так как ∆ 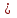0, то по теореме Крамера система имеет единственное решение.
Вычислим определители матриц , , 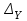, 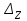полученных из матрицы А заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:
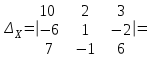
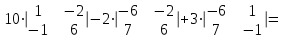
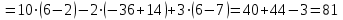
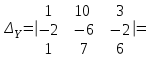
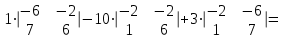
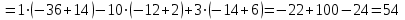
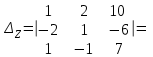
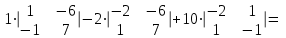
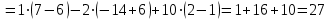
Теперь по формулам Крамера
; ; ,
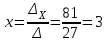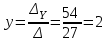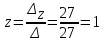т.е. решение системы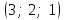
2) метод Гаусса
Расширенная матрица системы имеет вид:
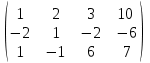
Умножая первую строку на 2 и прибавляя полученную строку ко второй, исключим переменную х1 из второй строки:
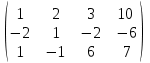
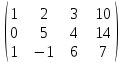
Умножая первую строку на (-1) и прибавляя полученную строку к третьей, исключим переменную х1 из третьей строки:
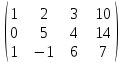
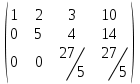
Получим систему уравнений
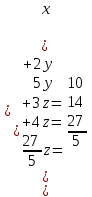
откуда, используя обратный ход метода Гаусса, найдем из третьего уравнения
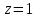; из второго уравнения 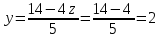и из первого уравнения 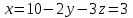, т.е. решение системы (3; 2; 1)Задача 5
Найти ранг матрицы
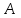размерностью 4×4. Найти определитель матрицы: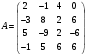 Шаг 1
Так как
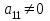, то умножая первую строку матрицы соответственно на числа 1,5, -2,5, 0,5, и прибавим полученные строки соответственно ко второй и третьей строкам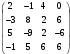 
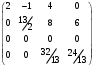
Третья строка состоит сплошь из нулей, поэтому, вычеркнув ее, получим матрицу
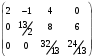,ранг которой равен 3. Ранг исходной матрицы также равен 3.
Так как ранг квадратной матрицы меньше количества строк матрицы, то ее определитель равен нулю.
Задача 6
Составить систему из двух уравнений с двумя неизвестными так, чтобы она:
а) имела единственное решение;
b) не имела решений;
с) имела бесконечно много решений.
Найти определители этих систем. Учитывая, что каждое из уравнений системы является уравнением прямой линии на плоскости, изобразить эти прямые и пояснить, что означает каждый из трех вариантов с точки зрения взаимного расположения прямых
Решение
а)
; 
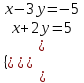
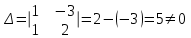
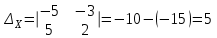
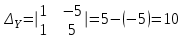
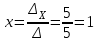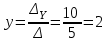
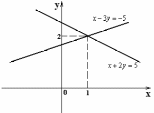
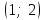- точка пересечения прямых 
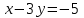и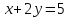 
Система имеет единственное решение
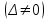
b)
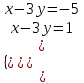
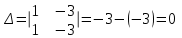
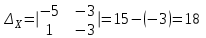
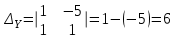
Система не имеет решений
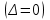
Прямые
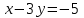и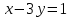 
не пересекаются, являются параллельными. с)
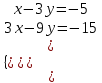
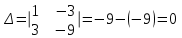
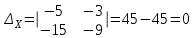
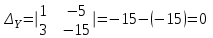
Система имеет множество решений
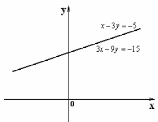
Прямые
и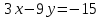 
совпадают.Задача 7
Найти точку пересечения прямых
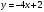и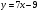 
.Решение
Для нахождения координат точки пересечения прямых необходимо решить систему уравнений
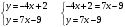
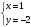
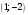- точка пересечения прямых 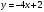и 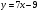.Задача 8
Найти уравнения прямой, проходящих через точку
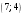параллельной и перпендикулярной к прямой 
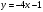. Найти расстояние от точки до данной прямой.Решение
Угловой коэффициент прямой
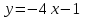равен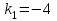 
. Найдем угловой коэффициент
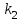перпендикуляра из условия перпендикулярности двух прямых: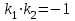 
Подставляя вместо
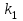угловой коэффициент данной прямой, получим: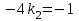 
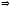
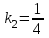. Так как перпендикуляр проходит через точку
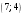и имеет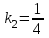
, то будем искать его уравнение в виде
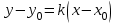. Подставляя
; 
; 
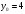, получим: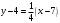 
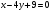- уравнение прямой перпендикулярной к 
.Найдем угловой коэффициент
параллельной прямой из условия: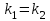 
,тогда
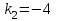. Так как параллельная прямая проходит через точку
и имеет 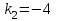, то будем искать его уравнение в виде 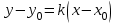. Подставляя
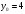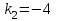; ; , получим: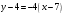 
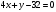- уравнение прямой параллельной .Для нахождения длины расстояния воспользуемся формулой для определения расстояния
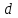от точки 
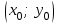до прямой 
:
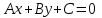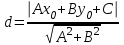
Подставляя
; ; 
; 
; 
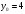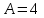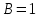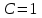, получим
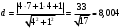
Задача 9
Найти уравнение плоскости, проходящей через точки
, 
, 
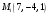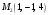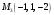
Уравнение плоскости найдем по формуле:
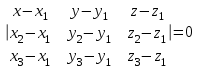
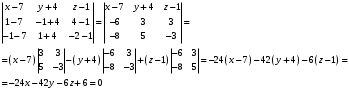
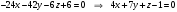
Таким образом,
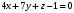- уравнение плоскости, проходящей через точки 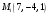, , 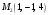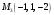.Задача 10
Какая кривая описывается уравнением
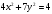. Написать каноническое уравнение этой кривой. Решение
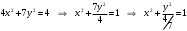- уравнение эллипса с полуосями 
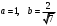. Центр эллипса – точка 
.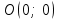