Файл: Моделирование в научных исследованиях стало использоваться еще в глубокой древности и постепенно захватывало все новые области научных знаний.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 104
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– составить упрощенную математическую модель взаимоотношений хищника и жертвы в природном сообществе.
Начальная численность популяции зайца (жертвы) – 1000 особей. Nз0 = 1000. Начальная численность популяции волка (хищник) – 20 особей. Nв0 = 20. Выжившая к концу каждого года часть популяции зайца увеличивает свою численность на 30 %. Рз = 0,3. Годовой прирост популяции волков – 10%. Рв = 0,1. Один волк потребляет по 40 зайцев ежегодно. R1в = 40. Смертность зайца по иным причинам равна нулю. Смертность волков равна нулю.
Задача №1.
Условие. Рассчитать, какова будет численность популяции зайца через 1,3,5 и 10 лет при полном отсутствии волков. Отобразить изменения численности зайцев в течение данного периода графически.
Решение.
Nз0 = 1000 Nз = Nз0 + Nз0 * Рз
Рз = 0,3; Nз = ?
Используем ячейки В5 – В15.
Формула для вычислений : В6 = $A$1 =B5+B5*$B$1.
Ячейки В7 – В15 заполняем вниз по образцу.
Задача №2.
Условие. Рассчитать, какова будет численность популяции зайца через 1, 3,5 и 10 лет, если начальная численность волков составляет 20 особей и не изменяется на протяжении указанного времени. Отобразить изменения численности зайцев в течение данного периода графически. Сравнить результат с результатами задачи №1.
Решение.
Nз0 = 1000 Nз = (Nз0 - Nв0* R1в) + (Nз0 - Nв0* R1в)* Рз
Рз = 0,3 Nз = (Nз0 - Nв0* R1в) * (1+ Рз)
Nв0 = 20.
R1в = 40.
Рв = 0.
Nз = ?
Для популяции волков используем ячейки F 5 – F 15.
Присваиваем F5 = $C$1. Дальше копируем вниз по образцу (популяция волка не меняется по условию).
Для популяции зайцев используем ячейки С5 – С15.
Присваиваем С5 = $C$1.
Формула: С6 = (C5-F5*$D$1)*(1+$B$1). Ячейки С7 – С15 заполняем вниз по образцу.
Задача №3.
Условие. Рассчитать, какова будет численность популяции зайца через 1, 3,5 и 10 лет, если начальная численность волков составляет 20 особей и возрастает на 10% ежегодно Отобразить изменения численности зайцев в течение данного периода графически. Сравнить результат с результатами задачи №1и №2.
Решение
.
Nз0 = 1000 Nз = (Nз0 - Nв* R1в) + (Nз0 - Nв0* R1в)* Рз
Рз = 0,3 Nз = (Nз0 - Nв* R1в) * (1+ Рз)
Nв0 = 20. Nв = Nв0 + Nв0* Рв
R1в = 40.
Рв = 0,1.
Nз = ? Для популяции волков используем ячейки G5 – G15.
Присваиваем G5 = $C$1. G6 =G5+G5*$E$1.
Для популяции зайцев используем ячейки D5 – D15.
Присваиваем D5 = $A$1.
Формула: D6 =(D5-G5*$D$1)*(1+$B$1). Ячейки D7 – D15 заполняем вниз по образцу.
Задача №4.
Условие. Рассчитать, какой должна быть начальная численность растущей популяции волков, чтобы численность зайцев была относительно стабильной (то есть равнялась приблизительно 1000) в течение первых пяти лет существования популяции. Как будет изменяться численность популяции зайца в течение следующих пяти лет? Представьте данные графически.
Решение.
Nз0 = 1000 Nз = Nз0
Рз = 0,3 Nз = (Nз - Nв* R1в) * (1+ Рз)
R1в = 40. Nв = Nв0 + Nв0* Рв
Рв = 0,1.
Nв0 = ? Для популяции волков ячейки H5 – H15.
В задаче требуется подобрать такое начальное количество волков, при котором численность зайцев будет минимально изменяться в течение первых пяти лет существования. Подбирать начальное число будем в ячейке Н1. Поэтому ячейке Н5 присваиваем значение $H$1.
H5 = $H$1. H6 =H5+H5*$E$1.
Для популяции зайцев используем ячейки
E5 – E15.
E5 = $A$1.
Формула: E6 =(E5-H5*$D$1)*(1+$B$1). Ячейки E7 – E15 заполняем вниз по образцу.
Изменяя число в ячейке Н1, подбираем значения в ячейках Е5 – Е9 примерно равные 1000.
Такими значениями будут 5 и 6. Наиболее удачное значение – 6 (начальная популяция волков).
Составление электронной таблицы
В первую строку таблицы вносим константы, входящие в условие :
A1 – начальная численность зайцев, Nз0 = 1000.
B1 – ежегодное увеличение популяции зайцев, Рз = 0,3 .
C1 – начальная численность волков, Nв0 = 20.
D1 – количество зайцев, поедаемых одним волком за год, R
1в = 40.
E1 – годовой прирост численности волков, Рв = 0,1.
Решение запишем в ячейки, расположенные ниже.
В экологии начальным годом принято считать «нулевой» год, поэтому годы пронумеруем от 0 до 10.
В ячейки B5 – F5 присваиваем $A$1 – начальная численность зайцев, Nз0. В ячейки F5, G5 присваиваем $C$1 – начальная численность волков, Nв0 .
(В первом задании волки не упоминаются, ячейка H5 заполняется отдельно по условию задачи № 4) .
Рис.2.1 Первоначальный вид электронной таблицы.
Рис.2.2. Заполненная электронная таблица.
Рис.2.3. Электронная таблица с рассчитанными значениями.
Графическое представление данных. Для построения графиков воспользуемся Мастером диаграмм: по оси Х откладываем номер года, по оси У – численность популяции. Все диаграммы должны располагаться в первой четверти.
Для большей наглядности графики к задачам №1, №2, №3 выстроим на одном листе. Это позволит наглядно увидеть разницу в колебаниях численности популяции зайца и сделать правильные выводы.
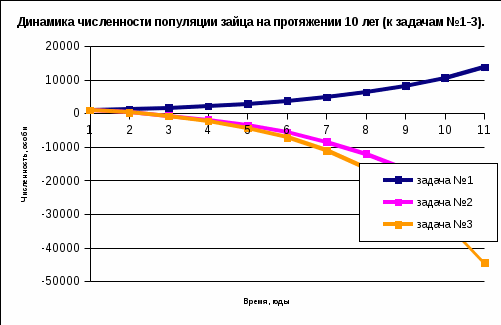
Рис.2.4. Электронная таблица с рассчитанными значениями.
Заключение
В ходе написания курсовой работы были выполнены все задачи, которые были поставлены вначале исследования. Изучены основные понятия о компьютерном моделировании; систематизирован материал по компьютерному моделированию в области математики; рассмотрено компьютерное моделирование на примере решения задачи хищник-жертва.
Исходя из анализа данных компьютерного эксперимента, можно сделать выводы о том, что компьютерное моделирование позволяет нам прогнозировать численность популяций, изучать влияние различных факторов на популяционную динамику. В приведенном примере мы исследовали модель «хищник-жертва», влияние коэффициента рождаемости жертв на численность оленей и волков. Небольшой прирост популяции жертв приводит к небольшому увеличению жертв, которую через некоторый период уничтожают хищники. Умеренный прирост популяции жертв приводит к увеличению численности обеих популяций. Высокий прирост популяции жертв приводит сначала к быстрому росту популяции жертв, это влияет на увеличение роста хищников, но затем расплодившиеся хищники быстро уничтожают популяцию оленей. В итоге оба вида вымирают.
Начальная численность популяции зайца (жертвы) – 1000 особей. Nз0 = 1000. Начальная численность популяции волка (хищник) – 20 особей. Nв0 = 20. Выжившая к концу каждого года часть популяции зайца увеличивает свою численность на 30 %. Рз = 0,3. Годовой прирост популяции волков – 10%. Рв = 0,1. Один волк потребляет по 40 зайцев ежегодно. R1в = 40. Смертность зайца по иным причинам равна нулю. Смертность волков равна нулю.
Задача №1.
Условие. Рассчитать, какова будет численность популяции зайца через 1,3,5 и 10 лет при полном отсутствии волков. Отобразить изменения численности зайцев в течение данного периода графически.
Решение.
Nз0 = 1000 Nз = Nз0 + Nз0 * Рз
Рз = 0,3; Nз = ?
Используем ячейки В5 – В15.
Формула для вычислений : В6 = $A$1 =B5+B5*$B$1.
Ячейки В7 – В15 заполняем вниз по образцу.
Задача №2.
Условие. Рассчитать, какова будет численность популяции зайца через 1, 3,5 и 10 лет, если начальная численность волков составляет 20 особей и не изменяется на протяжении указанного времени. Отобразить изменения численности зайцев в течение данного периода графически. Сравнить результат с результатами задачи №1.
Решение.
Nз0 = 1000 Nз = (Nз0 - Nв0* R1в) + (Nз0 - Nв0* R1в)* Рз
Рз = 0,3 Nз = (Nз0 - Nв0* R1в) * (1+ Рз)
Nв0 = 20.
R1в = 40.
Рв = 0.
Nз = ?
Для популяции волков используем ячейки F 5 – F 15.
Присваиваем F5 = $C$1. Дальше копируем вниз по образцу (популяция волка не меняется по условию).
Для популяции зайцев используем ячейки С5 – С15.
Присваиваем С5 = $C$1.
Формула: С6 = (C5-F5*$D$1)*(1+$B$1). Ячейки С7 – С15 заполняем вниз по образцу.
Задача №3.
Условие. Рассчитать, какова будет численность популяции зайца через 1, 3,5 и 10 лет, если начальная численность волков составляет 20 особей и возрастает на 10% ежегодно Отобразить изменения численности зайцев в течение данного периода графически. Сравнить результат с результатами задачи №1и №2.
Решение
.
Nз0 = 1000 Nз = (Nз0 - Nв* R1в) + (Nз0 - Nв0* R1в)* Рз
Рз = 0,3 Nз = (Nз0 - Nв* R1в) * (1+ Рз)
Nв0 = 20. Nв = Nв0 + Nв0* Рв
R1в = 40.
Рв = 0,1.
Nз = ? Для популяции волков используем ячейки G5 – G15.
Присваиваем G5 = $C$1. G6 =G5+G5*$E$1.
Для популяции зайцев используем ячейки D5 – D15.
Присваиваем D5 = $A$1.
Формула: D6 =(D5-G5*$D$1)*(1+$B$1). Ячейки D7 – D15 заполняем вниз по образцу.
Задача №4.
Условие. Рассчитать, какой должна быть начальная численность растущей популяции волков, чтобы численность зайцев была относительно стабильной (то есть равнялась приблизительно 1000) в течение первых пяти лет существования популяции. Как будет изменяться численность популяции зайца в течение следующих пяти лет? Представьте данные графически.
Решение.
Nз0 = 1000 Nз = Nз0
Рз = 0,3 Nз = (Nз - Nв* R1в) * (1+ Рз)
R1в = 40. Nв = Nв0 + Nв0* Рв
Рв = 0,1.
Nв0 = ? Для популяции волков ячейки H5 – H15.
В задаче требуется подобрать такое начальное количество волков, при котором численность зайцев будет минимально изменяться в течение первых пяти лет существования. Подбирать начальное число будем в ячейке Н1. Поэтому ячейке Н5 присваиваем значение $H$1.
H5 = $H$1. H6 =H5+H5*$E$1.
Для популяции зайцев используем ячейки
E5 – E15.
E5 = $A$1.
Формула: E6 =(E5-H5*$D$1)*(1+$B$1). Ячейки E7 – E15 заполняем вниз по образцу.
Изменяя число в ячейке Н1, подбираем значения в ячейках Е5 – Е9 примерно равные 1000.
Такими значениями будут 5 и 6. Наиболее удачное значение – 6 (начальная популяция волков).
Составление электронной таблицы
В первую строку таблицы вносим константы, входящие в условие :
A1 – начальная численность зайцев, Nз0 = 1000.
B1 – ежегодное увеличение популяции зайцев, Рз = 0,3 .
C1 – начальная численность волков, Nв0 = 20.
D1 – количество зайцев, поедаемых одним волком за год, R
1в = 40.
E1 – годовой прирост численности волков, Рв = 0,1.
Решение запишем в ячейки, расположенные ниже.
В экологии начальным годом принято считать «нулевой» год, поэтому годы пронумеруем от 0 до 10.
В ячейки B5 – F5 присваиваем $A$1 – начальная численность зайцев, Nз0. В ячейки F5, G5 присваиваем $C$1 – начальная численность волков, Nв0 .
(В первом задании волки не упоминаются, ячейка H5 заполняется отдельно по условию задачи № 4) .
| | A | B | C | D | E | F | G | H | I | J | |||||||
| 1 | 1000 | 0,3 | 20 | 40 | 0,1 | | | | | ||||||||
| 2 | Зайцы (условие) | Волки (условие) | | | | | | ||||||||||
| 3 | Годы | Зайцы | Волки | | | ||||||||||||
| 4 | | Задача1 | Задача2 | Задача3 | Задача4 | Задача2 | Задача3 | Задача4 | | | |||||||
| 5 | 0 | =$A$1 | =$A$1 | =$A$1 | =$A$1 | =$C$1 | =$C$1 | | | | |||||||
| 6 | 1 | | | | | | | | | | |||||||
Рис.2.1 Первоначальный вид электронной таблицы.
| | A | B | C | D | E | F | G | H | I | |
| 1 | 1000 | 0,3 | 20 | 40 | 0,1 | | Nв0 | | ||
| 2 | Зайцы (условие) | Волки (условие) | | | | | ||||
| 3 | Годы | Зайцы | Волки | | ||||||
| 4 | | Задача1 | Задача2 | Задача3 | Задача4 | Задача2 | Задача3 | Задача4 | | |
| 5 | 0 | $A$1 | $A$1 | $A$1 | $A$1 | $C$1 | $C$1 | $H$1 | | |
| 6 | 1 | =B5+B5*$B$1 | =(C5-F5*$D$1)*(1+$B$1) | =(D5-G5*$D$1)*(1+$B$1) | =(E5-H5*$D$1)*(1+$B$1) | $C$1 | =G5+G5*$E$1 | =H5+H5*$E$1 | | |
| 7 | 2 | | | | | $C$1 | | | | |
| 8 | 3 | | | | | $C$1 | | | | |
Рис.2.2. Заполненная электронная таблица.
| | A | B | C | D | E | F | G | H | I | |||||
| 1 | 1000 | 0,3 | 20 | 40 | 0,1 | | 6 | | ||||||
| 2 | Зайцы (условие) | Волки (условие) | | | | | ||||||||
| 3 | Годы | Зайцы | Волки | | ||||||||||
| 4 | | Задача1 | Задача2 | Задача3 | Задача4 | Задача2 | Задача3 | Задача4 | | |||||
| 5 | 0 | 1000 | 1000 | 1000 | 1000 | 20 | 20 | 6 | | |||||
| 6 | 1 | 1300 | 260 | 260 | 988 | 20 | 22 | 6,6 | | |||||
| 7 | 2 | 1690 | -702 | -806 | 941,2 | 20 | 24,2 | 7,26 | | |||||
| 8 | 3 | 2197 | -1952,6 | -2306,2 | 846,04 | 20 | 26,62 | 7,986 | | |||||
| 9 | 4 | 2856,1 | -3578,38 | -4382,3 | 684,58 | 20 | 29,282 | 8,7846 | | |||||
| 10 | 5 | 3712,93 | -5691,89 | -7219,65 | 433,1548 | 20 | 32,2102 | 9,66306 | | |||||
| 11 | 6 | 4826,809 | -8439,46 | -11060,5 | 60,62212 | 20 | 35,43122 | 10,62937 | | |||||
| 12 | 7 | 6274,852 | -12011,3 | -16221 | -473,918 | 20 | 38,97434 | 11,6923 | | |||||
| 13 | 8 | 8157,307 | -16654,7 | -23114 | -1224,09 | 20 | 42,87178 | 12,86153 | | |||||
| 14 | 9 | 10604,5 | -22691,1 | -32277,6 | -2260,12 | 20 | 47,15895 | 14,14769 | | |||||
| 15 | 10 | 13785,85 | -30538,4 | -44413,1 | -3673,84 | 20 | 51,87485 | 15,56245 | | |||||
Рис.2.3. Электронная таблица с рассчитанными значениями.
Графическое представление данных. Для построения графиков воспользуемся Мастером диаграмм: по оси Х откладываем номер года, по оси У – численность популяции. Все диаграммы должны располагаться в первой четверти.
Для большей наглядности графики к задачам №1, №2, №3 выстроим на одном листе. Это позволит наглядно увидеть разницу в колебаниях численности популяции зайца и сделать правильные выводы.
Анализ данных.

Рис.2.4. Электронная таблица с рассчитанными значениями.
Заключение
В ходе написания курсовой работы были выполнены все задачи, которые были поставлены вначале исследования. Изучены основные понятия о компьютерном моделировании; систематизирован материал по компьютерному моделированию в области математики; рассмотрено компьютерное моделирование на примере решения задачи хищник-жертва.
Исходя из анализа данных компьютерного эксперимента, можно сделать выводы о том, что компьютерное моделирование позволяет нам прогнозировать численность популяций, изучать влияние различных факторов на популяционную динамику. В приведенном примере мы исследовали модель «хищник-жертва», влияние коэффициента рождаемости жертв на численность оленей и волков. Небольшой прирост популяции жертв приводит к небольшому увеличению жертв, которую через некоторый период уничтожают хищники. Умеренный прирост популяции жертв приводит к увеличению численности обеих популяций. Высокий прирост популяции жертв приводит сначала к быстрому росту популяции жертв, это влияет на увеличение роста хищников, но затем расплодившиеся хищники быстро уничтожают популяцию оленей. В итоге оба вида вымирают.