ММОК-224

Туребаев Қуаныш

14 сұрақ. 6 - сыныпта математика курсында экстремумге берілген қолданбалы есептерді шешу әдістері.

Жауабы:

6 - сынып математикасында қарапайым экстремумға берілген есептерді кездестіруге болады. Негізгі мектептің төменгі сыныптарының оқушыларына тек бір ғана шешімі бар есептерден бөлек, бірнеше шешімі бар есептер де беріледі. Ондай кездерде тағы қосымша сұрақ қою керек: шешімдердің ішінен ең тиімдісін таңдаңыз, дәлірек айтқанда экстремумға берілген есепті шешу керек. Ондай есептермен оқушылар «Теңсіздіктер», «Тіктөртбұрыштың ауданы мен периметрі», «Натурал сандар», « Натурал сандардың бөлінгіштік қасиеттері» деген тарауларды оқу барысында кездеседі.

6-сыныпта «Математика» оқу пәнінің базалық мазмұнына шамалы өзгерістер енгізілген. Атап айтқанда, қолданыстағы оқу бағдарламасы бойынша 6-сыныпта қарастырылатын «функция» ұғымына қатысты тарау 7-сыныпқа көшірілген. Осы тараудың орынан 6-сыныпта «Шамалар арасындағы тәуелділіктер» тарауы қарастырылады және келесі тақырыптардан тұрады: «Шамалар арасындағы тәуелділіктерді беру тәсілдері: аналитикалық (формула арқылы), кестелік, графиктік тәсіл», «Нақты процестердің графиктерін қолданып шамалар арасындағы тәуелділіктерді зерттеу», «Тура пропорционалдық және оның графигі». Осыған байланысты «Екі айнымалысы бар сызықтық теңдеулер мен олардың жүйелері» бөліміне өзгерістер енгізілген. Яғни осы тарауда екі айнымалысы бар сызықтық теңдеу және оның графигі, екі айнымалысы бар сызықтық теңдеулер жүйелері, екі айнымалысы бар сызықтық теңдеулер жүйесін қосу тәсілімен және алмастыру тәсілімен шешу, есептерді сызықтық теңдеулер жүйелері арқылы шығару материалдары ғана қарастырылады.

Бағалау әдісі алгебралық және геометриялық экстремалды есептерді шешуде орын алады. Әдістің мәні келесідей. Белгілі бір өрнек (немесе белгілі бір геометриялық F фигурасы) қарастырылады, осы өрнекті (немесе F фигурасын) сипаттайтын бір немесе бірнеше шама бөлінеді. Таңдалған мәнді немесе мәндер жиынын бағалау, яғни z мәні пішіннің теңсіздіктерінің бірін қанағаттандыратынын дәлелдеу қажет.

z 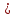M или z 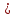m (1)

мұндағы m және M есеп шарттарымен анықталады.

Есепті шешу үшін (1) теңсіздіктердің біреуінің дұрыстығын анықтау қажет, яғни (1) теңсіздіктердің біріне жататын әрбір z үшін бұл өрнек мағынасы бар екенін дәлелдеу керек (F фигурасы бар) және теңсіздікті қанағаттандырмайтын кез келген z саны үшін бұл өрнек мағынасы жоқ (F фигурасы жоқ). Мәселені шешудегі соңғы қадам m және M экстремалды мәндерін анықтау болып табылады.

---

Дискретті функцияны азайту үшін 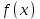, х 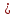С,, мұнда аналитикалық түрде көрсету кейде қиын немесе мүмкін емес , таңдау әдісі қолданылады. Бұл әдістің мәні мынада: біріншіден, 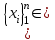С нүктелерінің тізбегі таңдалады, содан кейін 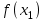, , 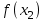, 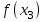…, 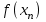функциясының барлық мәндері дәйекті түрде есептеледі. Бұл есептеулер k болғанша жалғасады, 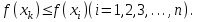сонда 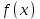= 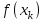.екені анық.

Есептер шығару:

1. 
   Асқар екі бірдей шеңберді тік бұрышты үшбұрышпен байланыстыра отырып келесідей сызбаға тап болды. Фигураның штрихталған бөлігінің ауданын табыңыз, мұндағы жарты шеңбердің диаметрлері өзара перпендикуляр.
   

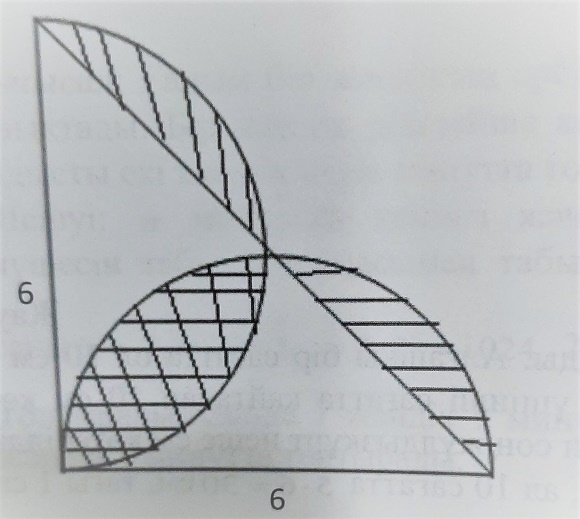
Шешуі:

Төмендегі фигураны былай орналастырамыз:



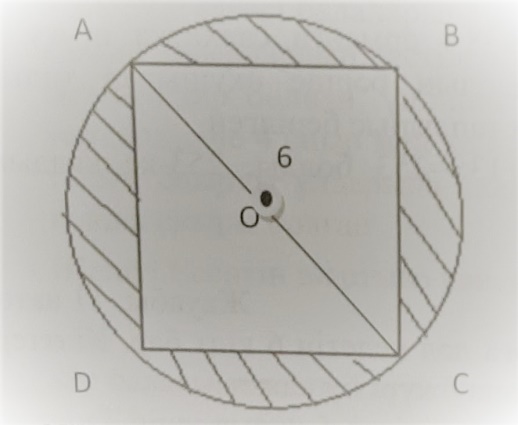
сонда штрихталған фигураның ауданы:

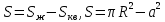
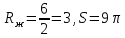енді квадраттың ауданын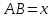



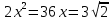
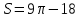
Жауабы:

2. 
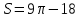
   Гүлсезім гүл егу үшін, алдымен жердің өлшемдері бойынша сызбасын сызып алды және әріптермен белгілеп шықты.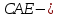 жарты шеңбер 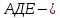теңбүйірлі тік бұрышты үшбұрыш. 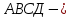квадрат, 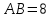болса, гүл егетін жердің ауданын табыңыз (сызбада штрихталған бөлігіне ғана гүл егіледі).
   

---

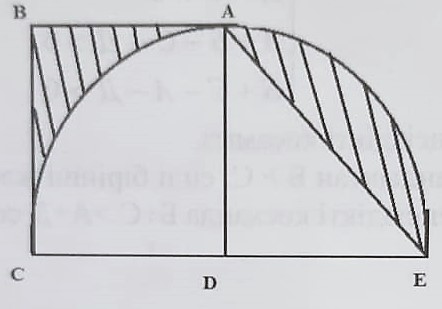
Шешуі:

Фигураны былай орналастырсақ:



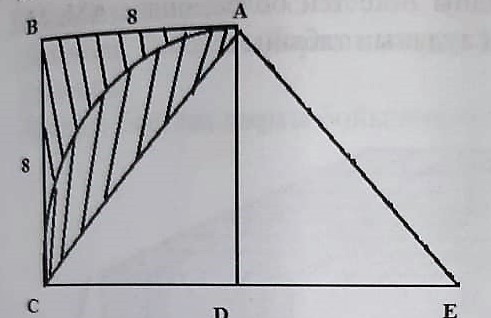
сонда, штрихталған фигураны квадраттың жартысы болады.



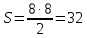
Жауабы:

---

Смотрите также файлы

• Программа среднего профессионального образования 44. 02. 03. А педагогика дополнительного образования (в области социальнопедагогической деятельности) Дисциплина Психология Практическое занятие 3.rtf

• Рабочая программа по курсу внеурочной деятельности Проектная деятельность.docx

• Ложка это ложка, Ложкой суп едят.docx

• 1 Определим расход на каждом участке.docx

• Курсовой проект по теме разработка модуля учёта продаж тюнинг запчасти для автомобилей.docx