Гидродинамика – раздел гидравлики (механики жидкостей), в котором изучаются законы движения жидкостей и пути их применение при решении конкретных задач. В гидродинамике широко используется термин «идеальная жидкость», законы движения которой применяются и к реальным жидкостям с учетом влияния вязкости. Основной задачей гидродинамики является определение скорости жидкости и давления в конкретной точке в зависимости от координат и времени.
Основные понятия и определения гидродинамики

Движение жидкости характеризуется скоростью движения частиц и давлением. Различают два вида движения: установившееся и неустановившееся. При установившемся скорость U и давление P в данной точке не меняются с течением времени, а зависят только от положения рассматриваемой точки, являясь функцией координат:

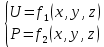. (3.1)

При неустановившемся движении скорость и давление зависят еще и от времени t:

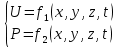. (3.2)

Линия тока – воображаемая линия в каждой точке которой вектор скорости касателен к ней.

Траектория движения частицы -
Трубка тока -

Элементарная струйка –

Свойство эл. стр.-

Важнейшее свойство трубки тока – непроницаемость её поверхности для движущихся частиц жидкости (ведь эта поверхность образована линиями тока!).

Если контур Lограничивает бесконечно малую площадку, струйка называется элементарной. Элементарная струйка имеет малую площадь поперечного сечения dω, которая может меняться по длине.

Совокупность элементарных струек образует поток жидкости.
Гидравлические характеристики живого сечения потока
Объем жидкости, проходящий через сечение dω за единицу времени, называют объемным расходом элементарной струйки dQ:

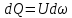. (3.11)

Расход потока жидкости равен сумме расходов элементарных струек, составляющих поток:

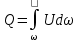. (3.12)

Скорость U в различных точках поперечного сечения, очевидно, может быть неодинаковой. Для характеристики движения всего потока вводится понятие

---

средней по сечению скорости, определяемой как v=Q/ω. То есть

Q=ωv. (3.13)

Живое сечение потока - поверхность, нормальная в каждой точке её к направлению скорости. Живое сечение может быть плоским или криволинейным.

Смоченным периметром χ называют ту часть полного периметра сечения, по которой жидкость соприкасается с твердыми стенками.

Гидравлическим радиусом называют отношение

R=ω/χ. (3.14)

Уравнение неразрывности
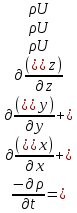. (3.15)

Выражение (3.15) - искомое уравнение неразрывности. При установившемся движении плотность от времени не зависит и 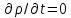. Поэтому уравнение неразрывности примет вид

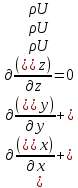. (3.16)

Для несжимаемой жидкости (ρ=const) уравнение неразрывности

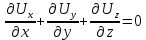. (3.17)

Неразрывность движения применительно к элементарной струйке жидкости
dQ =const

U₁dω₁ =U₂dω₂ = const. (3.22)
Таким образом, объемный расход жидкости остается неизменным на всем протяжении элементарной струйки.

Так как расход потока жидкости равен сумме расходов элементарных струек, условие сплошности (неразрывности) потока для несжи­маемой жидкости можно записать в виде

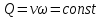.(3.23)

Для двух живых сечений потока уравнение (3.23) можно записать в виде

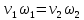. (3.23а)

4.1. Дифференциальные уравнения движения невязкой жидкости
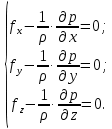Добавим ед. силы инерции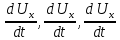

В результате получим уравнения Эйлера для движения сплошной среды:

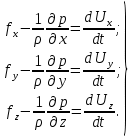(4.2)

Три уравнения (4.2) содержат четыре неизвестные функции U_x,U_y,U_z и p. Поэтому для решения системы необходимо еще одно уравнение, связывающее эти функции. Такое уравнение есть – это уравнение неразрывности (3.15) (или (3.17) для несжимаемой жидкости).

---

Для несжимаемой жидкости (ρ=const) уравнение неразрывности


4.7. Уравнение Д. Бернулли для струйки невязкой жидкости


Умножим уравнения (**) соответственно на dx, dy и dz и сложим:






.

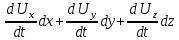
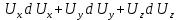
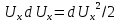
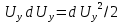
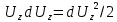
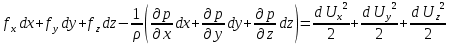
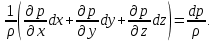
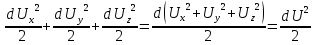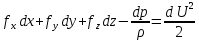
Если движение происходит только под действием силы тяжести





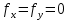
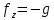
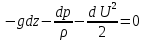
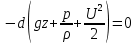
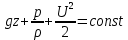, (4.26)

или, после деления на g,

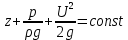. (4.27)

Выражение (4.27) - уравнение Бернулли для струйки установившегося движения идеальной несжимаемой жидкости.

Иногда уравнение (4.27) называют законом Бернулли, поскольку оно представляет следствие закона сохранения энергии для стационарного потока идеальной несжимаемой жидкости.

Здесь z - геометрическая высота центра тяжести сечения струйки над горизонтальной плоскостью x0y; p/ρg - пьезометрическая высота; U²/2g - скоростная высота.

4.8. Геометрическое и энергетическое истолкование

уравнения Бернулли для невязкой жидкости
Проясним геометрический смысл уравнения Бернулли (4.27) для элементарной струйки идеальной жидкости:

---

.

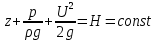Все слагаемые уравнения имеют размерность длины.

Член уравнения z определяет высоту центра тяжести рассматриваемого сечения над горизонтальной плоскостью сравнения. Его называют геометрической высотой или геометрическим напором.

Член уравнения p/ρg называют пьезометрической высотой или пьезометрическим напором.

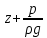- называют гидростатическим напором.
Член уравнения U²/2g называют скоростной высотой или скоростным напором.



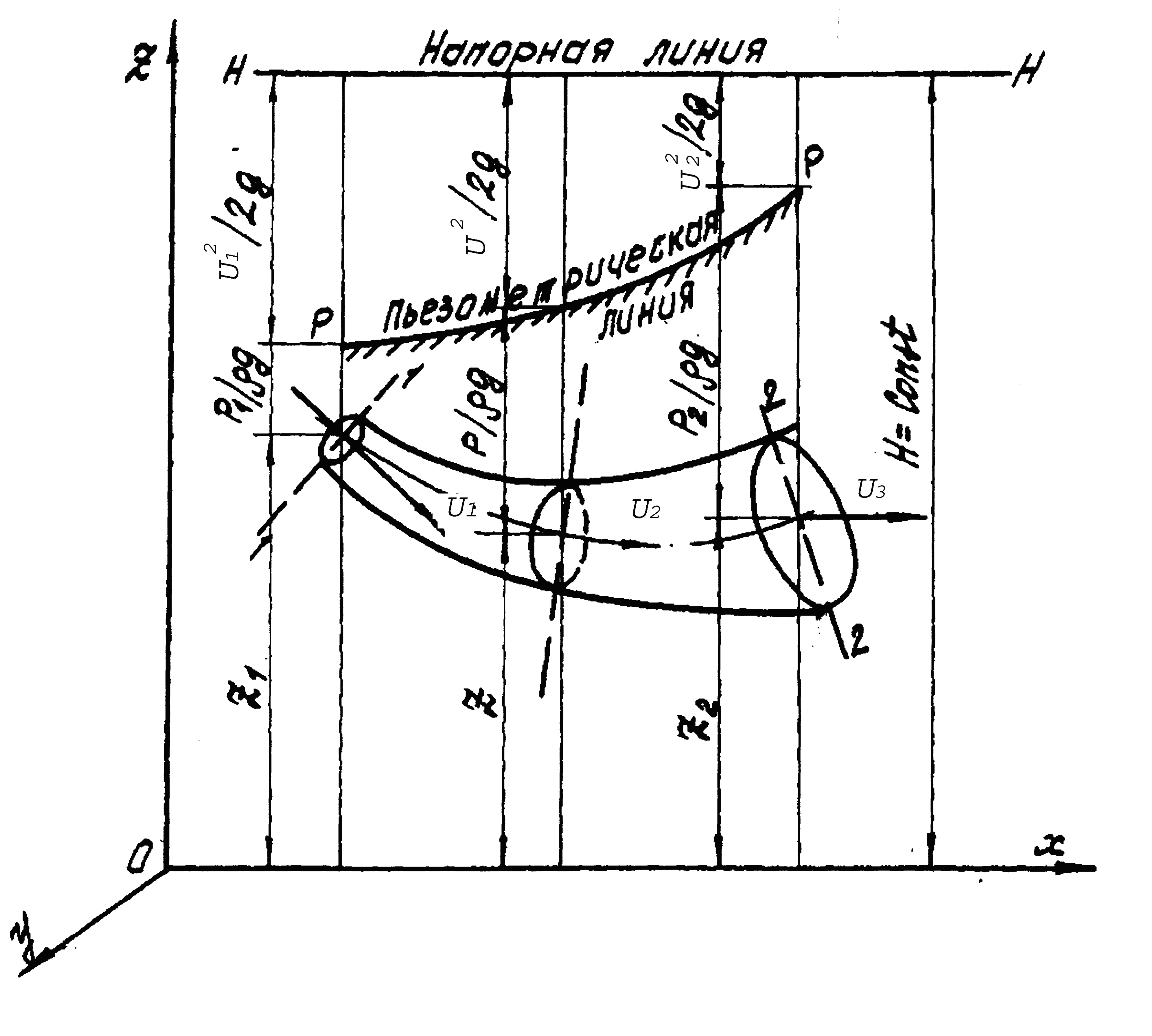
Рис. 4.3




Трёхчленная сумма H - полный (гидродинамический) напор в данном сечении струйки.

Слагаемые уравнения Бернулли изображают в системе координат xyz (рис. 4.3), откладывая от горизонтальной плоскости x0y геометрические напоры z, пьезометрические p/ρg и скоростные U²/2g высоты.
Соединив концы отрезков, выражающих скоростные напоры U²/2g, получим линию H-H, называемую напорной или линией полного напора.

Соединив концы отрезков, выражающих пьезометрические высоты p/ρg, получим пьезометрическую линию Р-Р. Эта линия изображает изменение суммы геометрической и пьезометрической высот вдоль струйки.

Рассмотрим Энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости. Напишем уравнение для двух произвольных сечений 1-1 и 2-2:

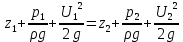. (4.27)

Таким образом, слагаемые уравнения Бернулли выражают работу единицы веса жидкости, так как удельные работы эквивалентны удельным энергиям. Следовательно:

z - удельная (потенциальная) энергия положения,

p/ρg - удельная (потенциальная) энергия давления,

z+p/ρg - удельная потенциальная энергия,

U²/2g - удельная кинетическая энергия.

Из (4.27) следует, что полная удельная энергия H постоянна вдоль струйки идеальной жидкости.

4.9. Уравнение Бернулли для струйки реальной жидкости

---

уравнение Бернулли для струйки реальной жидкости:

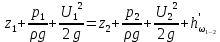. (4.34)

Как видим, в случае реальной жидкости полный напор вдоль струйки не остаётся постоянным, а убывает в направлении движения. Поэтому график уравнения Бернулли для струйки реальной жидкости (рис. 4.4) отличается от аналогичного графика для идеальной жидкости (рис. 4.3).
4.10. Уравнение Бернулли для потока реальной жидкости

.
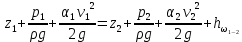Величина α - коэффициент Кориолиса (корректив кинетической энергии) - отношение действительной кинетической энергии потока к кинетической энергии, которой обладал бы поток при том же расходе, если бы все частицы жидкости двигались с одной и той же (средней) скоростью. Коэффициент α зависит от степени неравномерности распределения скоростей по сечению. Для ламинарного течения в круглой цилиндрической трубе α=2, для турбулентного течения α≈1.05÷1.1.

Однако при существенной неравномерности эпюры скоростей коэффициент α может оказаться и более значительным.
Выражение (4.39) - уравнение Бернулли для потока однородной вязкой несжимаемой капельной жидкости при установившемся плавно изменяющемся движении.

Уравнение (4.39) выражает закон изменения кинетической энергии применительно к одномерным задачам гидромеханики.

Уравнение (4.39) выведено при условии плавной изменяемости потока в выбранных расчетных сечениях. На участке потока между сечениями это условие может нарушаться.

Последний член правой части уравнения (4.39) выражает усредненную потерю удельной механической энергии (потерю напора) между сечениями 1–1 и 2–2.

Уравнению (4.39) можно дать геометрическую трактовку, построив график (диаграмму) уравнения Бернулли для потока вязкой жидкости (рис. 4.6).

4.11. Гидравлический и пьезометрический уклоны

Для характеристики относительного изменения полного напора по длине потока вводят понятие гидравлического уклона.

Средний гидравлический уклон на участке между сечениями 1–1 и 2–2 (рис. 4.6) определяется как отношение потери напора к длине участка:

,

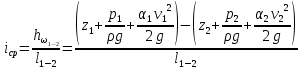где l_1-2 - расстояние (по пути движения) между сечениями 1–1 и 2–2.

Гидравлический уклон - безразмерная положительная величина.

Гидравлический уклон в сечении потока определяется выражением

---

Смотрите также файлы

• Разработайте программу наблюдения.docx

• Нравственное содержание правовых норм.docx

• Практикум 1 Финтех опыт банка Тинькофф Выполнил студент группы дбэ101 Пушкарский Родион.docx

• спасательные средства и выживание на море индивидуальные и коллективные спасательные средства.pdf

• Управление силами и средствами при тушении пожаров в музеях, библиотеках, выставках.docx