ФГБОУ ВОУральский государственный университет путей сообщения(УрГУПС)Кафедра «Естественнонаучные дисциплины»Отчет по компьютерной лабораторной работе № 1.3. «Закон сохранения механической энергии»Студент Соколова ОксанаГруппа __________________________________________________________Преподаватель ___________________(Фишбейн Л.А.)Дата_________________________Екатеринбург2023Цели и задачи:

• 
  Знакомство с применением физических моделей – консервативная и диссипативная механическая система.
  
• 
  Экспериментальная проверка закона сохранения механической энергии в консервативных и диссипативных системах.
  

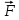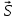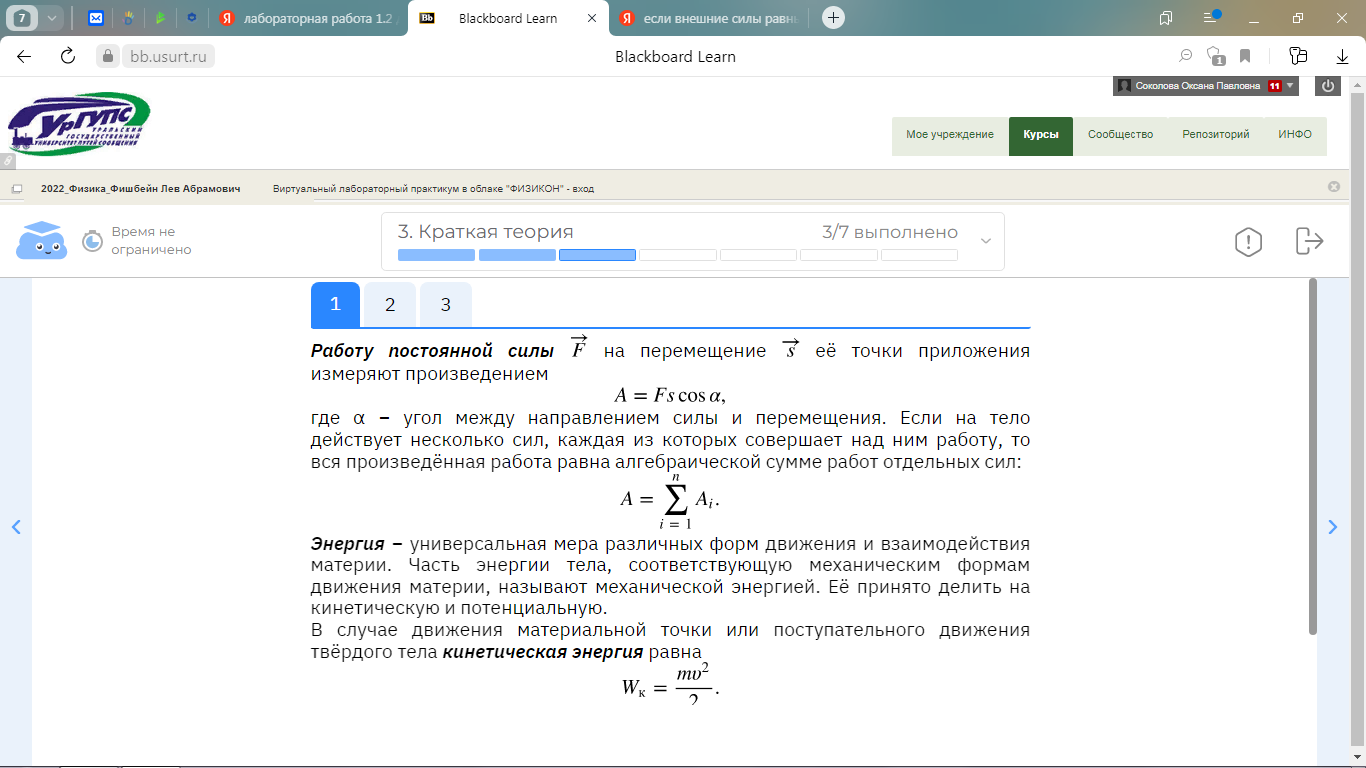
Описание экспериментальной установки – компьютерное моделированиеТеоретическая частьРаботу постоянной силы   на перемещение  её точки приложения измеряют произведением где α – угол между направлением силы и перемещения. Если на тело действует несколько сил, каждая из которых совершает над ним работу, то вся произведённая работа равна алгебраической сумме работ отдельных сил: Энергия – универсальная мера различных форм движения и взаимодействия материи. Часть энергии тела, соответствующую механическим формам движения материи, называют механической энергией. Её принято делить на кинетическую и потенциальную.В случае движения материальной точки или поступательного движения твёрдого тела 

---

кинетическая энергия равнаПотенциальная энергия  W_п – часть механической энергии, обусловленная взаимным расположением тел или частей тела и их взаимодействием друг с другом.Полная механическая энергия системы тел равна арифметической сумме кинетических и потенциальных энергий всех тел, входящих в данную систему: Консервативными называются силы, работа которых при перемещении тела из одного состояния в другое не зависит от того, по какой траектории произошло это перемещение.Если работа по перемещению тела зависит от траектории перемещения из одной точки в другую, то такая сила называется диссипативной.Теорема о кинетической энергии: изменение кинетической энергии равно работе всех сил, действующих на это тело.Теорема о потенциальной энергии: работа консервативных сил равна изменению потенциальной энергии системы, взятому с противоположным знаком.

Aконс = –(Wп2 – Wп1).

Закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется:W_полн = const.Если на тело в процессе его перехода из одного состояния в другое кроме консервативных сил (сил тяготения и упругости) действуют другие силы, то изменение полной механической энергии равно работе этих сил:

ΔWполн = Wполн2 – Wполн1 = ΣA.

Задание: Модель: (с данными для бригады № 6)

---

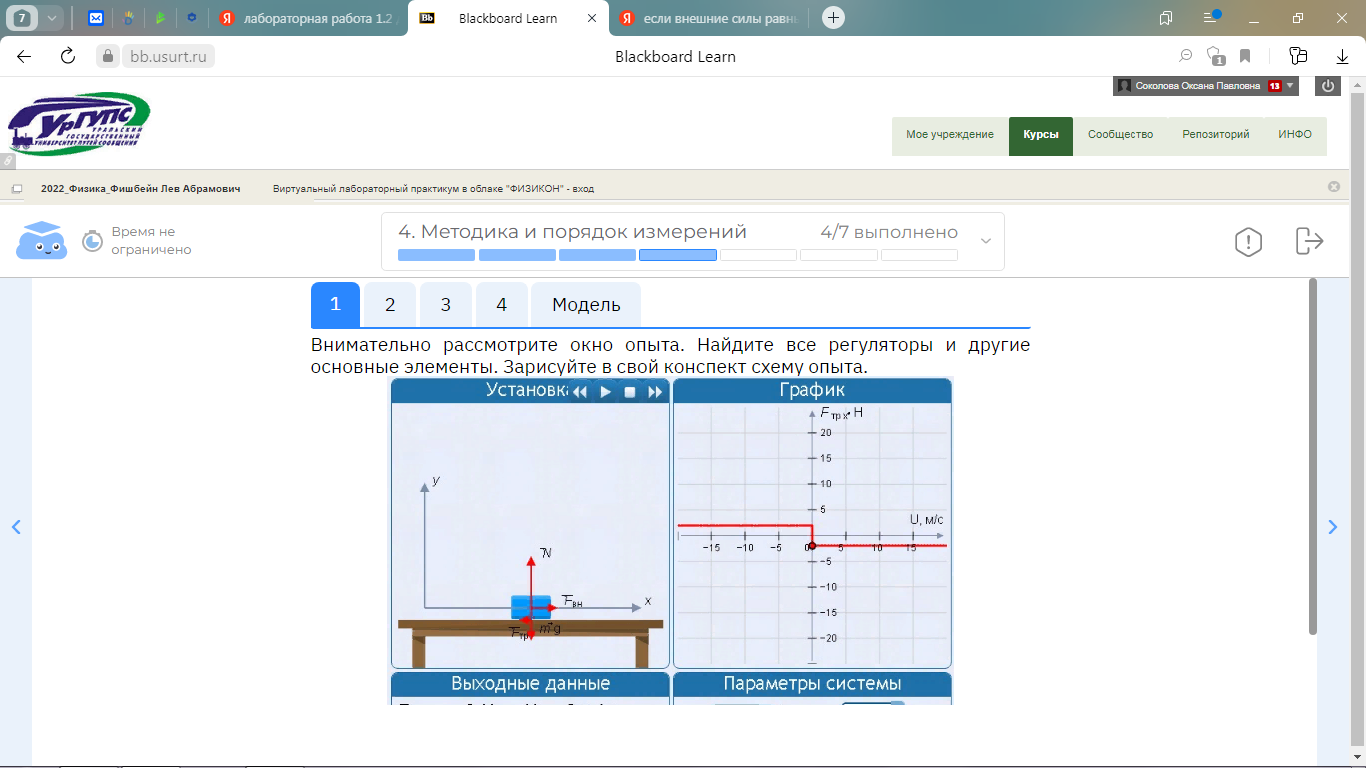
Компьютерная модель «Движение по наклонной плоскости»Исходные данные: бригада № 6.

иг., бригада 6 m, кг 3,0 μ 0,3 α, ° 30 Fвн, Н 2 a, м/с2

Таблица 1. Исходные параметры опыта

Экспериментальная частьТаблица 2. Исходные параметры опыта

m = 3,0 кг , μ = 0,3 , α = 300 , Fвн = 2 Н
t	υ	S	Wк	Wп	Aтр	Aвн	Aсум	∆Wполн

РасчетыВывод.Лабораторная работа выполнена самостоятельно, при помощи алгоритма данного в виртуальной лабораторной работе.Для знакомство с теорией использована литература:

1. 
   Трофимова Т. И. Курс физики. М.: Высшая школа, 2006. Гл. 2, § 5–8.
   
2. 
   Детлаф А. А., Яворский Б. М. Курс физики. М.: Высшая школа, 2000. Гл. 2, § 2.1–2.5.
   

---

Смотрите также файлы

• Примечание Пеня за просрочку обязательств устанавливается контрактом в размере 1300 ключевой ставки цб рф. При решении задания необходимо использовать 1300 ключевой ставки цб рф, равную 0,0167%.docx

• 16 Верно Баллов 1,00 из 1,00 Отметить вопрос Текст вопроса Какой учёный считал, что прямая линия, на которой дети рисуют предметы является тем ритмическим упрощением изображения пространства земли, которое доступно детскому пониманию Выберите один ответ a.docx

• Курсовая работа Договор куплипродажи недвижимости.rtf

• Отражение звука. Эхо.pptx

• .docx