Файл: Решение а уравнение ac б Найдем длину высоты, как расстояние от точки a до прямой bc.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 43
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
№1
Даны вершины A(5;3), B(-11;-9), C(-4;15) треугольника ABC. Найти:
а) уравнение AC
б) длину высоты, проведенной из вершины A
в) величину угла B (в радианнах)
Решение:
а) уравнение AC
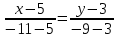
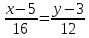
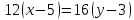
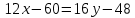
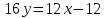
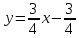
б)
Найдем длину высоты, как расстояние от точки A до прямой BC
Уравнение BC
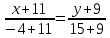
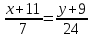
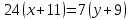
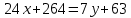
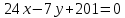
Формула расстояния от точки (
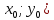до прямой Ax+By+C=0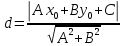
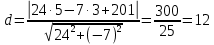
в)
величину угла B найдем как угол между векторами
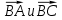
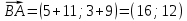
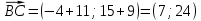
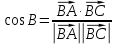
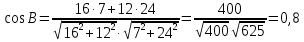
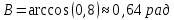
№2
Даны вершины поирамиды
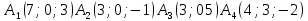
Найти:
а) длину ребра
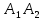
б) угол между ребрам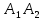и
и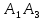
в) площадь грани
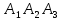
г) длину высоты пирамиды проведенной из вершины
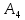
д) объём пирамиды
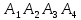
Решение:
а)
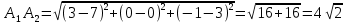
б)
угол
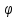между ребрами будем искть, как угол между векторами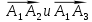 
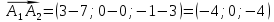
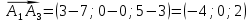
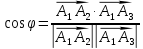
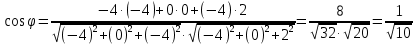
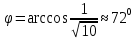
в)
площадь грани
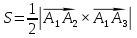
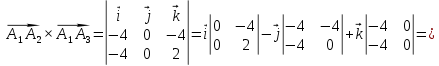
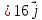
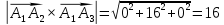
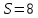
г)
Формула расстояния от точки (
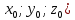до плоскости Ax+By+Cz+D=0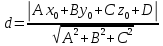
Запишем уравнение плоскости
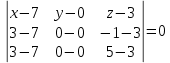
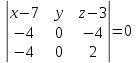
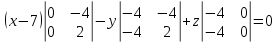
Получим
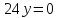
или
y=0
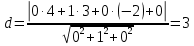
д)
объём пирамиды
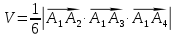
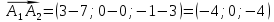
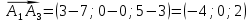
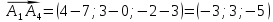
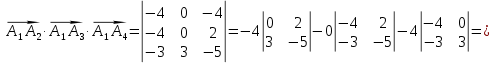
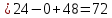
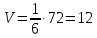
№3
Найти матрицу
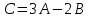
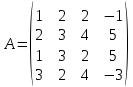
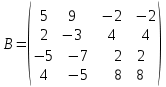
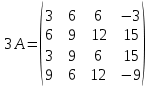
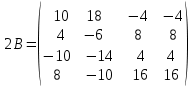
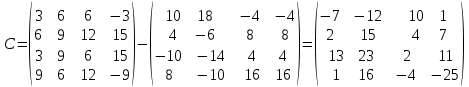
№4
Решить систему уравнений
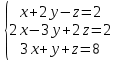
Метод Гаусса
Составим расширенную матрицу системы
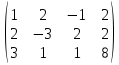
К 2 строке прибавим первую умноженную на -2
К 3 строке прибавим первую умноженную на -3
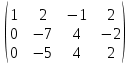
Поделим 2 сторку на -7
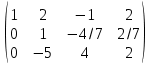
К 3 строке прибавим вторую умноженную на 5
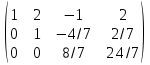
Поделим 3 строку на 8/7
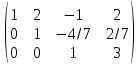
Прибавим к 2 строке третью умноженную на 4/7
Прибавим к 1 строке третью
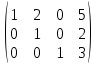
Прибавим к 1 строке вторую умноженную на -2
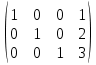
Получили
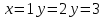
№5
Вычислить площадь фигуры ограниченной линиями
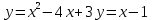
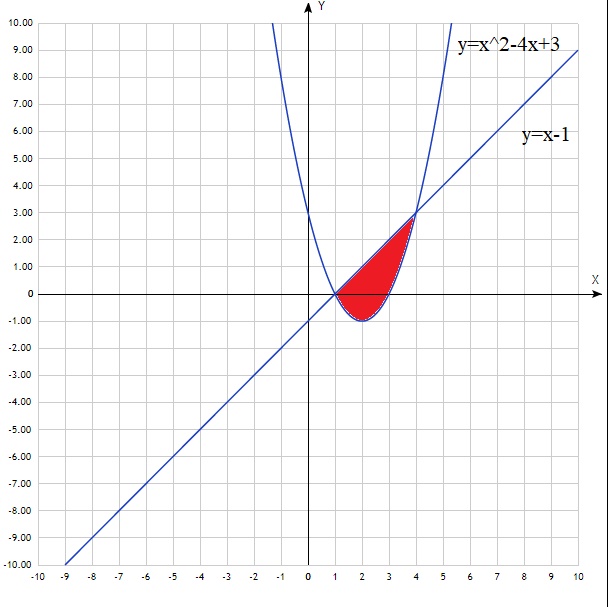
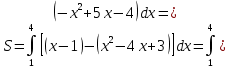
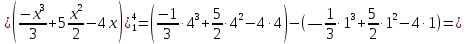
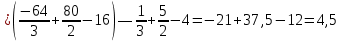
№6
| Вид ресурса | Затраты ресурса на единицу товара | Запас ресурса | ||
| 1 | 2 | 3 | ||
| Сырье | 3 | 5 | 2 | 260 |
| Рабочая сила | 22 | 14 | 18 | 400 |
| Оборудование | 10 | 14 | 8 | 128 |
| Прибыль | 30 | 25 | 56 | |
Составим математическую модель задачи
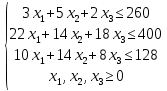
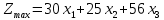
Решим данную задачу симплекс методом
преобразуем неравенства в равенства добавлением неотрицательных элементов
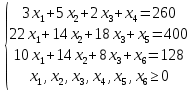
Составляем симплексную таблицу. В столбец x0 записывается правая часть ограничений. С правой стороны записывается матрица коэффициентов . Последняя строка - это целевая функция, умноженная на −1:
| Базис | X0 | X1 | X2 | X3 | X4 | X5 | X6 |
| X4 | 260 | 3 | 5 | 2 | 1 | 0 | 0 |
| X5 | 400 | 22 | 14 | 18 | 0 | 1 | 0 |
| X6 | 128 | 10 | 14 | 8 | 0 | 0 | 1 |
| | 0 | -30 | -25 | -56 | 0 | 0 | 0 |
Данный опорный план не является оптимальным, так как в пересечении строки 4 и столбцов , есть отрицательные элементы. Самый большой по модулю отрицательный элемент (-56), следовательно в базис входит вектор x3. Определяем, какой вектор выходит из базиса. Для этого вычисляем положительный min(260:2; 400:18; 128:8)=128:8 соответствует строке 3. Из базиса выходит вектор x6
| Базис | X0 | X1 | X2 | X3 | X4 | X5 | X6 |
| X4 | 260 | 3 | 5 | 2 | 1 | 0 | 0 |
| X5 | 400 | 22 | 14 | 18 | 0 | 1 | 0 |
| X3 | 128 | 10 | 14 | 8 | 0 | 0 | 1 |
| | 0 | -30 | -25 | -56 | 0 | 0 | 0 |
. Делим 3 строку на разрешающий элемент 8
| Базис | X0 | X1 | X2 | X3 | X4 | X5 | X6 |
| X4 | 260 | 3 | 5 | 2 | 1 | 0 | 0 |
| X5 | 400 | 22 | 14 | 18 | 0 | 1 | 0 |
| X3 | 16 | 5/4 | 7/4 | 1 | 0 | 0 | 1/8 |
| | 0 | -30 | -25 | -56 | 0 | 0 | 0 |
Прибавим к 1 строке 3 умноженную на -2
Прибавим к 2 строке 3 умноженную на -18
Прибавим к 4 строке 3 умноженную на 56
| Базис | X0 | X1 | X2 | X3 | X4 | X5 | X6 |
| X4 | 228 | 1/2 | 3/25 | 0 | 1 | 0 | -2/8 |
| X5 | 112 | -1/2 | -35/2 | 0 | 0 | 1 | -9/4 |
| X3 | 16 | 5/4 | 7/4 | 1 | 0 | 0 | 1/8 |
| | 896 | 40 | 73 | 0 | 0 | 0 | 7 |