ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 11
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Расчётно-графическая работа
Задание 2:
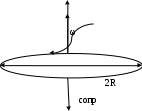
Стержень массой 550г и радиусом
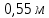вращается без начальной скорости вокруг своей оси. На стержень действуют пара сил с моментом 
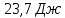и момент сопротивления 
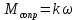, где 
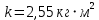. Сколько оборотов сделает стержень до того, как его угловая скорость станет равной 
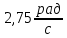. Построить графики зависимостей момента силы и угловой скорости от времени.Краткое теоретическое содержание
Явление, изучаемое в ргз – вращательное движение стержня относительно неподвижной оси, которая проходит через конец стержня.
Определение основных величин, процессов, явлений, объектов:
Ось вращения тела – прямая, на которой лежат центры окружностей, по которым движутся точки твердого тела при его вращении. Окружности, по которым движутся точки тела, лежат в плоскостях, перпендикулярных к этой оси.
Угловая скорость - векторная величина, характеризующая быстроту вращения, ориентацию оси вращения в пространстве и направление вращения. Модуль угловой скорости определяется формулой:
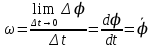
Единица угловой скорости [рад/с].
Угловое ускорение – векторная величина, характеризующая изменение угловой скорости со временем.
Момент инерции - величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. В механике различают моменты инерции осевые и центробежные. Осевым моментом инерции тела относительно оси z называется величина, определяемая равенством:
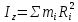или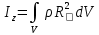 
где mi — массы точек тела, Ri — их расстояния от оси z, ρ — массовая плотность, V — объём тела. Величина Iz является мерой инертности тела при его вращении вокруг оси.
Пара сил – две равные по модулю и противоположно направленные силы, не действующие вдоль одной прямой.
Момент силы – векторная величина, модуль которой равен произведению силы на плечо:
, 
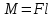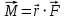. Если на тело действует 2 момента сил, вызывающих вращение в противоположном направлении, то один из них условно считают положительным, а второй отрицательным.Плечо – кратчайшее расcтояние от оси вращения до линии действия силы.
Законы, соотношения, использованные при решении
Второй закон Ньютона для вращательного движения
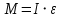; Угловая скорость
.Число оборотов равно:
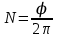, где N – число оборотов, φ – угол поворота.Модуль угловой скорости определяется формулой:
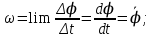где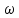 
- модуль угловой скорости; 
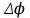- угол, на который поворачивается тело за промежуток времени 
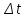.Угловое ускорение
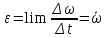
Момент инерции тела:
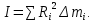
Момент инерции обруча:
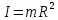.Модуль момента силы равен:
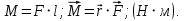где l – плечо.
Пояснение ко всем величинам, входящим в формулы и соотношения:
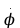- первая производная угла по времени; [
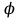]=рад.
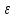- модуль углового ускорения; [ 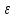]=рад/с
.
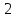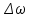- изменение угловой скорости за время 
; [
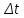]=рад/с.I - момент инерции тела; [I]=
.
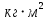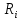- расстояние от оси до элементарной массы, м;
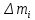- элементарная масса, кг;
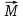- момент силы; [
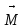] = Н∙м.
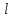- плечо; [ 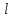] = м.F– сила, действующая на тело; [F] = Н.
N – число оборотов, совершаемое телом.
Решение поставленных задач
В основе данной расчетно-графической работы лежит вращательное движение стержня относительно неподвижной оси, которая проходит через центр тяжести.
По закону вращательного движения
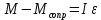(1).По определению угловое ускорение равно:
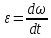
где ω - угловая скорость.
По условию
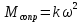. Формулу (1) перепишем в виде:
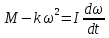
Воспользуемся соотношением
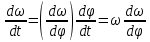
И подставим его в уравнение:
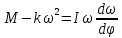
Разделим переменные в получившемся дифференциальном уравнении и проинтегрируем:
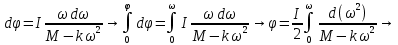
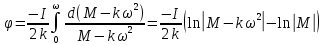
Число оборотов равно:
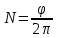
Подставляем:
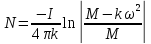
Момент инерции стержня:
где
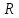– радиус стержня. Окончательно имеем: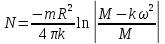
Проверка размерности:
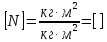
Подставим в формулу числовые значения и вычислим:
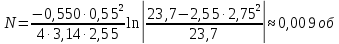
Графический материал
Определим аналитическую зависимость углового ускорения от времени.
;
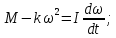
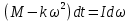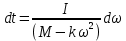;Проинтегрируем
;
;
;
;
;
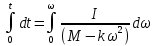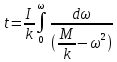
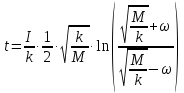
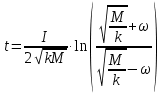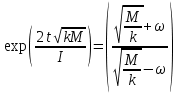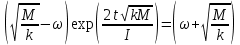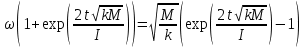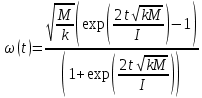
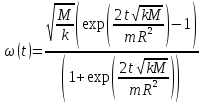
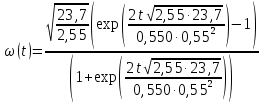
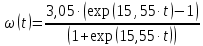
| t | ω |
| с | рад/с |
| 0 | 0 |
| 0,005 | 0,118509 |
| 0,01 | 0,236661 |
| 0,015 | 0,354102 |
| 0,02 | 0,470489 |
| 0,025 | 0,585489 |
| 0,03 | 0,698786 |
| 0,035 | 0,810083 |
| 0,04 | 0,919107 |
| 0,045 | 1,025607 |
| 0,05 | 1,12936 |
| 0,055 | 1,23017 |
| 0,06 | 1,327869 |
| 0,065 | 1,422318 |
| 0,07 | 1,513405 |
| 0,075 | 1,601046 |
| 0,08 | 1,685183 |
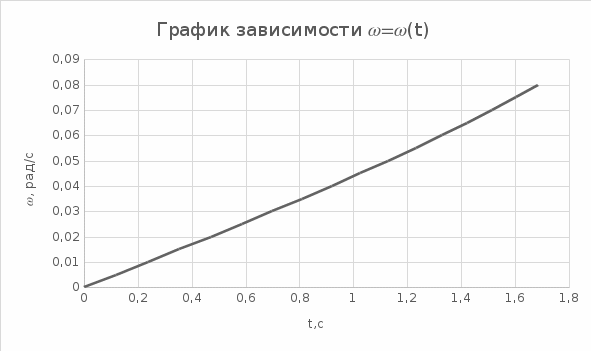
По условию задания на конус действует пара сил с постоянным моментом М, а соответственно М не зависит от времени t.
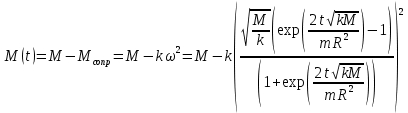
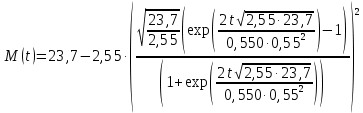
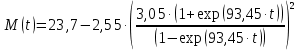
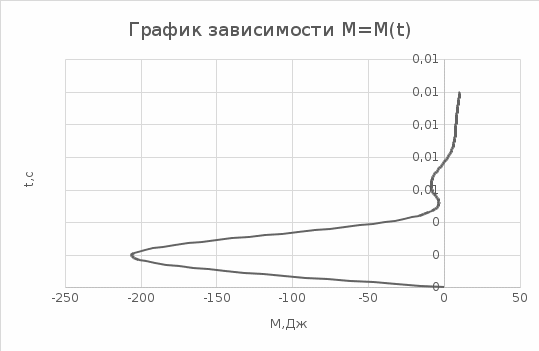
Анализ полученных результатов:
В результате проведённой работы делаю вывод, что стержень, вращающийся без начальной скорости, сделает 0,009 оборота до того, как его угловая скорость станет равной 2,75 рад/с.
Мною были построены графики зависимостей момента силы и угловой скорости от времени.