ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 14
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
№3.
????̇(????) = −????(????) + ????(????),
????(0) = -9,5
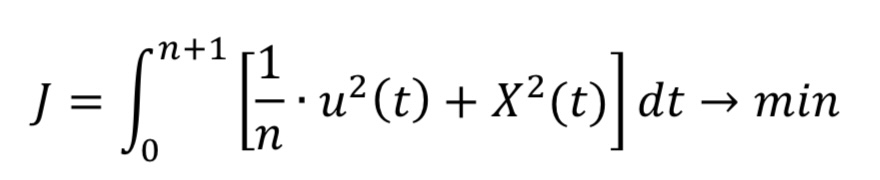
Здесь
x (x1, x2 )T R2 ,
t [0; 2], на управление наложено ограничение
| u| 1 , т.е.
uU
[1; 1] ,
f0 (t, x, u) 0 ,
F(t1, x) x2 ,
f1(t, x, u) x2 ,
f2 (t, x, u) x1 u, 1(t1, x(t1 )) t1 2 0 . Решается задача Майера.
-
Составляем гамильтониан H(t, , x, u) 1 x2 2 [ x1 u]. -
Находим максимум гамильтониана по управлению. Так как имеются ограничения на управление, требуется найти условный максимум гамильтониана по управлению. В данной задаче гамильтониан линеен по uна заданном отрезке изменения управления [-1; 1], поэтому оптимальное управление имеет вид
u(t) arg max H(t, (t), x(t), u) = 1 sign
(t)
1, 2(t) 0 ,
|u| 1
2 1,
2(t) 0 .
т.е. является релейным. Величина управления определяется знаком функции 2(t) .
-
Выписываем канонические уравнения (6) принципа максимума:
x1(t) x2 (t) , x1(0) 0 ,
x2 (t) x1(t) u(t) x1(t) sign 2(t),
x2(0) 0 ,
1
(t)
x1H(t, (t), x(t), u(t)) 2
(t) ,
2
(t)
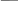x2H(t, (t), x(t), u(t)) 1
(t) .
-
Проверяем условия трансверсальности (5):
2 F H(t1 ) t1 j(t1 ) xj
0 ,
j1
t1 2
где
F(t1, x)
2 F(t1, x)
. Группируя члены, получаем
F
t1
t1
j1
xj
xj x2
H(2) t1 1 (2) x1 [1 2 (2)] x2
0 .
Момент окончания t1
задан, поэтому
t1 0 . Так как правый конец свободен, то
вариации
x1 ,
x2
считаются произвольными. Чтобы равенство выполнялось для
любых вариаций, необходимо, чтобы
1(2) 0 , 2(2) 1 .
-
Решаем двухточечную краевую задачу с учетом пп. 2 и 4:
x1(t) x2 (t) ,
x1(0) 0 ;
x2 (t) x1(t) sign 2 (t),
x2 (0) 0 ;
1(t) 2 (t) ,
1(2) 0 ;
2 (t) 1(t),
2(2) 1 .
Имеем:
1(t) sin t,
2(t) cos t,
u(t) sign ( cos t) sign (cos t) . Найденное
оптимальное управление
u(t)
на отрезке
[0, 2]
имеет две точки переключения и,
1
2
следовательно, три промежутка знакопостоянства:
-
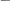при 0 t
2
, u(t) 1 ,
x(t) cos t 1 ,
x (t) sin t;
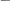- при
2
t 3
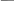2, u(t) 1 ,
x(t) cos t 2 sin t 1 ,
x (t) sin t 2 cos t;
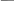- при 3
2
t 2,
u(t) 1 ,
x(t) cos t 4 sin t 1 ,
1
2
x(t) sin t 4 cos t.
Минимальное значение функционала равно x(2) 4 .