Файл: Лабораторная работа 4 "Теплообмен при пузырьковом кипении в жидкости" Выполнил студент гр. 325140210002 Поморцев А. С.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 36
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ПЕТРА ВЕЛИКОГО
Институт Энергетики
Высшая школа атомной и тепловой энергетики
Лабораторная работа № 2.4
"Теплообмен при пузырьковом кипении в жидкости"
Выполнил студент гр. 3251402/10002 Поморцев А.С.
студент гр. 3251402/10002 Рощин Е.Д.
студент гр. 3251402/10002 Теплинский А.К.
Преподаватель Павлов А.В.
Введение
Кипение – процесс перехода вещества из жидкого агрегатного состояния в газообразное. Обязательным условием для кипения является перегрев по всему объему или у поверхности нагрева. Если жидкость перегрета по всему объему, то возникает объемное кипение. Оно наблюдается при разгерметизации контуров энергоустановок или других объектов, в которых имеется нагретая жидкость под давлением. Объемное кипение не поддается регулировке, что приводит к аварийным ситуация.
Поверхностное кипение – упорядоченный процесс, который реализуется в котлах, бойлерах и других энергоустановках. В этом случае тепловой поток подводится со стороны поверхности, нагретой выше температуры насыщения. На поверхности возникают пузырьки пара, они растут, достигают отрывного диаметра и всплывают, затем на их месте возникают новые и процесс повторяется. На каждой стадии (возникновение, рост, отрыв и всплытие пузырька) коэффициент теплоотдачи α определяется разными факторами и потому может заметно меняться.
При исследовании кипения особая роль отводится эксперименту, и большинство расчетных формул по теплоотдаче при кипении основано на экспериментальных данных. Впервые эти данные обобщил в 1934 году Широ Нукияма в своей работе «Максимальное и минимальное количество тепла Q, переданного металлом кипящей воде при атмосферном давлении». Он построил зависимость плотности теплового потока от температурного напора ∆T= Tс - Tн, где Tс – температура стенки,Tн – температура насыщения (рис. 1).
В областях А и B кипение только развивается, наблюдаются отдельные пузыри. В области С развитое пузырьковое кипение, с регулярным образованием, отрывом и всплытием отдельных пузырей. Увеличение температурного напора приводит к частичному оттеснению жидкости от нагретой поверхности.
Пузыри объединяются, и часть разогретой поверхности теряет контакт с жидкостью, что приводит к резкому уменьшению плотности теплового потока и увеличению температуры поверхности нагрева (область Е). Этот процесс лавинообразный, вскоре вся поверхность нагрева покрывается паровой пленкой и начинается развитое пленочное кипение. Точку перехода от пузырькового кипения при повышении температурного напора к пленочному называют первой критической плотностью теплового потока.
В работе будет рассмотрен только режим пузырькового кипения (область С). При пузырьковом кипении паровые пузыри возникают в отдельных местах поверхности нагрева – центрах парообразования. Вырастая до определенного размера, паровые пузыри отрываются и всплывают в толще жидкости. При этом перегрев основной массы жидкости весьма невелик (≈ 0,01...0,1 °С).
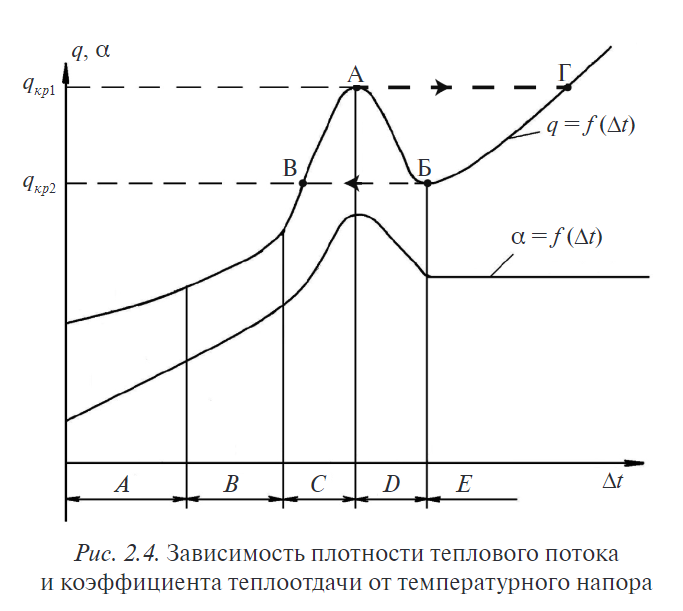
Рисунок 1 – Зависимость плотности теплового потока и коэффициента теплоотдачи от температурного напора
Результаты многочисленных экспериментальных исследований пузырькового кипения при умеренных тепловых потоках удовлетворительно обобщаются зависимостью
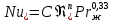 , (1)
, (1)Где
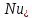 =
=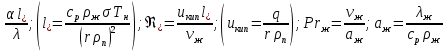 ;
; 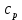 – удельная изобарная теплоемкость воды, Дж/(кг·К);
– удельная изобарная теплоемкость воды, Дж/(кг·К); 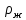 и
и 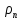 – плотности насыщенной жидкости и сухого насыщенного пара соответственно, кг/м3;
– плотности насыщенной жидкости и сухого насыщенного пара соответственно, кг/м3; 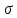 – коэффициент поверхностного натяжения, Н/м; r– скрытая теплота парообразования, Дж/кг; q– плотность теплового потока на поверхности нагрева, Вт/м2;
– коэффициент поверхностного натяжения, Н/м; r– скрытая теплота парообразования, Дж/кг; q– плотность теплового потока на поверхности нагрева, Вт/м2; 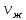 – кинематическая вязкость жидкости, м2/с;
– кинематическая вязкость жидкости, м2/с; 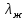
– теплопроводность жидкости, Вт/(м·К);
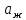 – температуропроводность жидкости).
– температуропроводность жидкости).Эмпирические константы в уравнении (1) принимают следующие значения: С = 0,0625, n = 0,5 (при
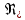 ≤ 0,01); С = 0,125, n = 0,65 (при
≤ 0,01); С = 0,125, n = 0,65 (при 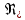 ≥ 0,01).
≥ 0,01).Формулу (1) можно применять для расчета теплоотдачи при кипении различных жидкостей. Для расчета теплоотдачи при кипении воды можно воспользоваться более простыми соотношениями:
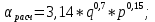 (2)
(2)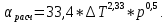 (3)
(3)В формулах (2) и (3) давление задается в барах (1 бар = 0,1 МПа), удельный тепловой поток – в Вт/м2, перегрев жидкости – в К или °С.
Это относится к процессу кипения в большом объеме:
– когда размеры области нагрева и диаметр пузырьков намного меньше размера сосуда, в котором происходит кипение;
– когда жидкость не движется вдоль поверхности нагрева.
Нарушение этих условий (например, при кипении в трубах) влияет на теплообмен и коэффициент теплоотдачи.
Описание установки
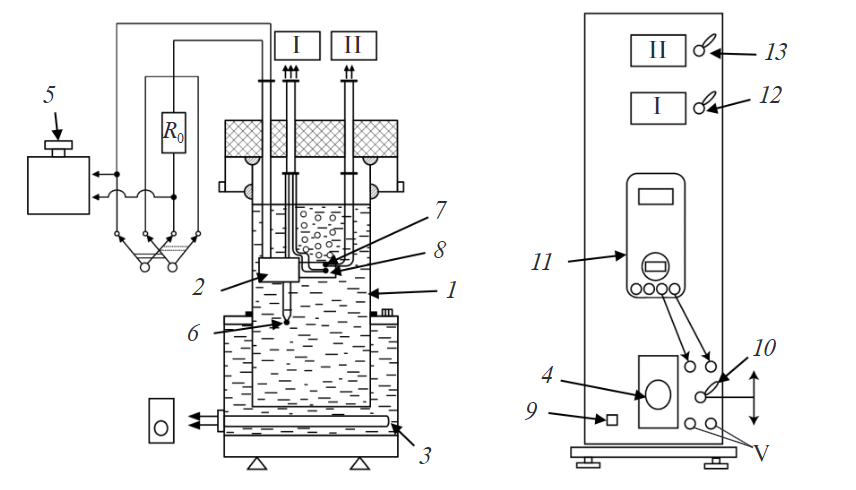
Рисунок 2 – Лабораторная установка для изучения пузырькового кипения: 1 – стеклянная емкость; 2 – экспериментальная модель; 3 – нагреватель; 4 – диммер; 5 – трансформатор; 6, 7, 8 – термопары (tж, t1, t2); 9 – тумблер электропитания; 10 – тумблер сопротивления; 11 – мультиметр; 12, 13 – тумблеры включения измерителей температуры
Результаты эксперимента
Таблица 1
Исходные данные
| Номер опыта | tж | t1 | t2 | Uн | U0 | I | Q |
| °С | В | мВ | А | Вт | |||
| 1 | 89,3 | 101,0 | 101,0 | 100 | 67 | 0,67 | 67,0 |
| 2 | 90,6 | 102,1 | 102,1 | 110 | 74 | 0,74 | 81,4 |
| 3 | 92,5 | 103,2 | 103,2 | 120 | 81 | 0,81 | 97,2 |
Обработка результатов
Далее приведется пример расчетов для второго режима.
1) Средняя температура поверхности цилиндра:
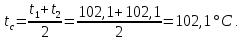
2) Тепловой поток, определяемый через мощность на нагревателе:

3) Средний коэффициент теплоотдачи от поверхности обогреваемого цилиндра к кипящей воде:
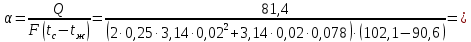
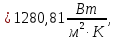
где
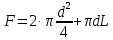 – площадь поверхности цилиндра, м2, d = 20 мм – диаметр цилиндра, L = 78 мм – длина цилиндра.
– площадь поверхности цилиндра, м2, d = 20 мм – диаметр цилиндра, L = 78 мм – длина цилиндра.4) Суммарная стандартная неопределенность измерения коэффициента теплоотдачи:
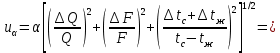
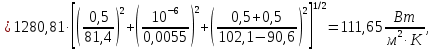
где
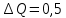 Вт,
Вт, 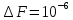 м2,
м2, 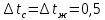 °С.
°С.Далее предлагается обобщить результаты опыта при помощи сравнения его результатов с расчетными.
1) Плотность теплового потока через поверхность цилиндра:
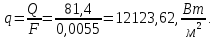
2) Теоретическое значение коэффициента теплоотдачи:
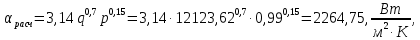
где p – атмосферное давление в барах.

Результаты вычислений для этого и остальных режимов приведены в Таблице 2.
Таблица 2
Результаты расчетов
| Номер режима | Q | 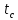 | 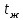 | α | q | p | αрасч | 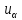 | |||||
| Вт | °С | 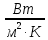 | 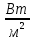 | Па | 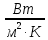 | 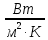 | |||||||
| 1 | 67,0 | 101,0 | 89,3 | 1036,21 | 12123,62 | 99308 | 2264,75 | 88,91 | |||||
| 2 | 81,4 | 102,1 | 90,6 | 1280,81 | 14729,30 | 99308 | 2595,40 | 111,65 | |||||
| 3 | 97,2 | 103,2 | 92,5 | 1643,77 | 17588,77 | 99308 | 2938,56 | 152,86 | |||||
Также по результатам расчетов строятся графики зависимостей
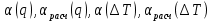 . Данные графики представлены на рисунках 2 и 3.
. Данные графики представлены на рисунках 2 и 3.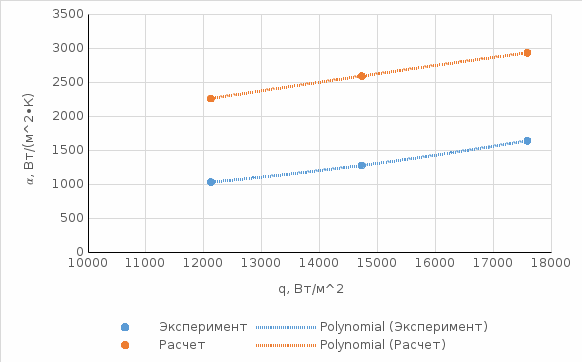
Рисунок 2 – График зависимостей
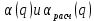
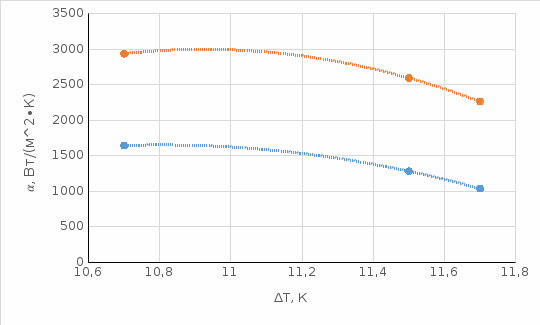
Рисунок 3 – График зависимостей
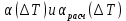
Данные графики демонстрируют сходство характеров расчетной и экспериментальной зависимостей, но кривые для опытного случая расположены вдоль вертикальной оси ниже, чем в случае расчетных данных.
Вывод
В результате эксперимента были получены значения коэффициента теплоотдачи от поверхности обогреваемого цилиндра к кипящей воде для трех разных режимов (
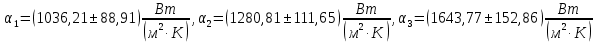 ).
).Также были построены графики зависимостей
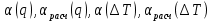 . Полученные зависимости имеют схожий характер, однако расчетные кривые располагаются ниже по вертикальной оси, чем теоретические. Данное расхождение можно объяснить неточностью измерения температуры воды и температур на поверхности цилиндра, а также наличием некоторых допущений при вычислении экспериментального коэффициента теплоотдачи.
. Полученные зависимости имеют схожий характер, однако расчетные кривые располагаются ниже по вертикальной оси, чем теоретические. Данное расхождение можно объяснить неточностью измерения температуры воды и температур на поверхности цилиндра, а также наличием некоторых допущений при вычислении экспериментального коэффициента теплоотдачи.Санкт-Петербург
2023