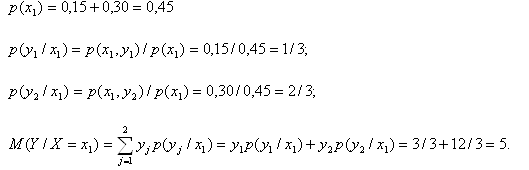Файл: Законы распределения и их применение в экономических расчётах (на примере любого закона распределения).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 35
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
экономического закона распределения по труду. Согласно этому закону доля работника в общественном продукте находится в прямой зависимости от количества и качества его труда, затраченного в процессе. Тарифная система — совокупность нормативных документов, регулирующих условия получения работником основной части заработной платы в целях обеспечения в масштабах общества необходимого единства меры труда и его оплаты при осуществлении закона распределения по труду.
Одной из важнейших форм создания материальной заинтересованности работников в результатах их труда является заработная плата. В. И. Ленин учил, что социализм строить необходимо ... не на энтузиазме непосредственно, а при помощи энтузиазма, рожденного великой революцией, на личном интересе, на личной заинтересованности . Заработная плата служит орудием осуществления экономического закона распределения по труду. Повышение ее наряду с расширением общественных фондов потребления обеспечивает рост благосостояния рабочих и служащих. Именно она должна быть основным источником роста доходов населения.
Экономический закон распределения по труду выражается в том, что труд оплачивается по его качеству и количеству. Качество труда определяется квалификацией рабочего, количество — его выработкой. Для оплаты труда по качеству служит тарифная система, по количеству — системы оплаты, связывающие заработок рабочего с объемом выполненной им работы. Системы оплаты. Заработная плата представляет собой мощную движущую силу роста производительности труда только в том случае, если отвечает требованиям экономического закона распределения по труду.
Вероятностно-статистические модели воспроизводят как устойчивые, так и временные зависимости между экономическими явлениями и факторами. Они позволяют обрабатывать статистические данные и исследовать законы распределения случайных экономических показателей.
Закон неуклонного роста производительности общественного
труда и закон распределения по труду реализуется в планировании производительности труда, установлении пропорций в распределении и использовании трудовых ресурсов, планировании фондов оплаты труда, общественных фондов потребления. [2, c.130]
Принцип материальной заинтересованности заключается в том, что на основе действующего при социализме экономического закона распределения по труду в зависимости от количества и качества его, на предприятиях кроме различных форм оплаты труда и премирования за счет фонда заработной платы образуются фонды материального поощрения и другие специальные фонды в сочетании с материальной ответственностью работников, предусмотренной в действующем хозяйственном и трудовом законодательстве.
График
Формула, описывающая нормальный закон распределения случайной величины, имеет следующий вид:
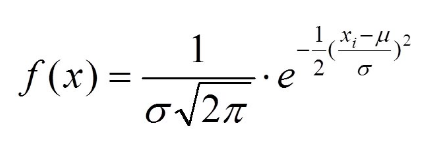
где: μ — генеральное среднее арифметическое; σ — генеральное стандартное отклонение, е — основание натуральных логарифмов, приблизительно равное 2,719, π — число, приблизительно равное 3,142; xi — конкретное значение признака.
Пусть Вас не пугает эта формула. Сейчас мы с ней разберемся. Для начала давайте посмотрим, как выглядит график, построенный на основе этой формулы. Зададим значения μ=0 и σ=1. Хочу заметить, что μ и σ — это просто числа. Их еще называют параметрами распределения. Поэтому критерии, в формулу расчета которых входят параметры распределения называют параметрическими. Например, параметрическим критерием является t-критерий Стьюдента. В формулу расчета критерия Стьюдента входят параметры μ и σ. Кривая нормального распределения вероятностей имеет вид (рис.1).
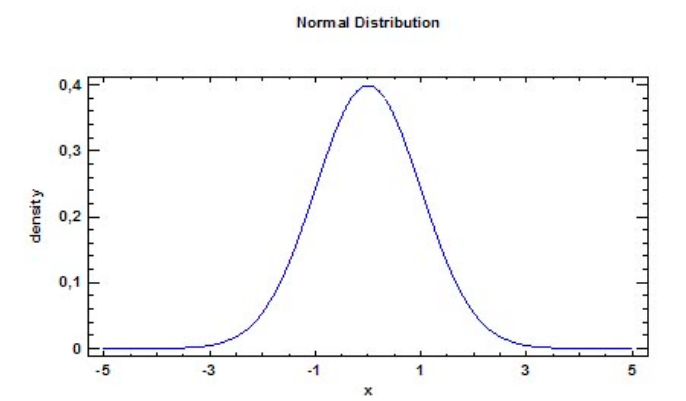
Рис.1 - График плотности вероятностей нормального распределения при μ=0 и σ=1.
Если мы поменяем параметры, то получим следующее. Изменение параметра μ будет сдвигать график вдоль оси Х. Например при μ=3 график сместится вправо вдоль оси Х (рис.2).
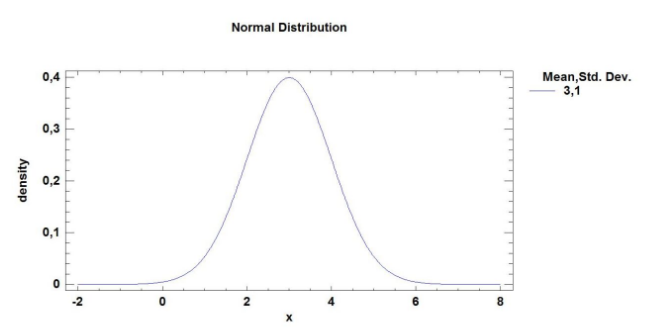
Рис.2 - График плотности вероятностей нормального распределения при μ=3 и σ=1.
Если оставим μ=0, а изменим параметр σ, например σ=3, то получим распределение с большим размахом (рис.3).
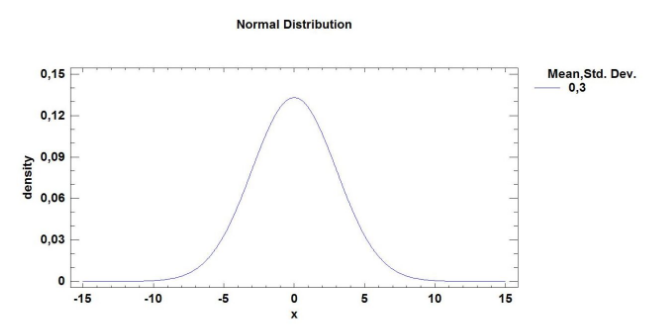
Рис.3 - График плотности вероятностей нормального распределения при μ=0 и σ=3.
Свойства нормального распределения
Нормальная кривая имеет колокообразную форму, симметричную относительно точки x=µ, с точками перегиба, абсциссы которых отстоят от µ на ± σ.
Нормальное распределение полностью определятся двумя параметрами: значением генерального среднего (µ) и генерального стандартного отклонения (σ).
Медиана и мода нормального распределения совпадают и равны µ.
Коэффициенты асимметрии и эксцесса нормального распределения равны нулю.
Нормированное отклонение
В области математической статистики важное место занимает нормированное отклонение (t) – показатель, представляющий отклонение той или иной варианты от средней величины, отнесенное к значению стандартного отклонения. Нормированное отклонение рассчитывает по формуле:
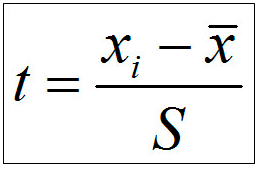
Нормированное отклонение позволяет установить, на сколько «сигм» отклоняются варианты от среднего значения. Например, необходимо определить насколько «сигм» отклоняется значение роста человека, равное 180 см от среднего, если среднее арифметическое равно 170 см, а «сигма», то есть стандартное отклонение равно 10 см. Подставив эти значения в формулу, получим: t= (180-170)/10 = 1.
Ответ: значение роста человека, равное 180 см отклоняется от среднего на одну «сигму».
Нормированное нормальное распределение
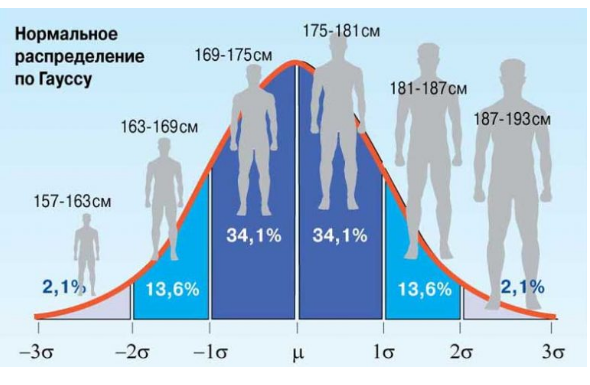
Рис.4 - Нормированное нормальное распределение роста мужчин с параметрами: µ=0; σ = 1.
Формула нормального распределения описывает целое семейство кривых, зависящих от двух параметров μ и σ, которые могут принимать любые значения. Поэтому возможно бесконечно много нормально распределенных совокупностей.
Чтобы избежать неудобств, связанных с расчетами для каждого конкретного случая в до компьютерную эпоху было предложено использовать нормированное (стандартное) нормальное распределение, для которого были составлены подробные таблицы. Нормированное нормальное распределение имеет параметры: µ=0; σ = 1 (рис.1, 5). Это распределение получается, если пронормировать нормально распределенную величину Х по формуле:
U= (X-μ)/σ.
Для нормированного нормального распределения характерно, что в интервал µ± σ попадают 68 % всех результатов, в интервал µ± 2σ попадают 95% всех результатов, в интервал µ± 3σ попадают 99 % всех результатов.
В области физической культуры и спорта эти закономерности используют для разработки системы оценок. Так, В.М.Зациорским (рис. 5) предложено использовать следующую систему оценок результатов. Если результат, показанный спортсменом, попал в интервал от -2σ до -1σ — он получает низкую оценку (Рассчитать, в какой интервал попадает результат можно при помощи нормированного отклонения. Это описано выше). Если результат попал в интервал от -1σ до -0,5σ — оценка ниже средней. Средний результат соответствует интервалу от -0,5σ до -0,5σ, результат, получивший оценку выше среднего — от 0,5 до 1σ. Высокий результат попадает в интервал от 1σ до 2σ.
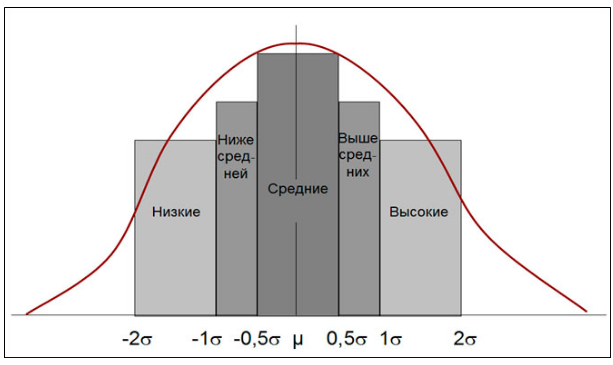
Рис.5 - Анализ
Свойства распределения
Чтобы проверить, соответствует ли распределение нормальному закону, существует много методов.
Можно использовать свойства нормального распределения (равенство среднего, моды и медианы).
Однако более точные результаты дают критерии согласия. В зависимости от объема выборки (n) следует использовать различные критерии:
Числовые характеристики
Условные законы распределения.
Как было показано выше, зная совместный закон распределения можно легко найти законы распределения каждой случайной величины, входящей в систему.
Однако, на практике чаще стоит обратная задача – по известным законам распределения случайных величин найти их совместный закон распределения.
В общем случае эта задача является неразрешимой, т.к. закон распределения случайной величины ничего не говорит о связи этой величины с другими случайными величинами.
Кроме того, если случайные величины зависимы между собой, то закон распределения не может быть выражен через законы распределения составляющих, т.к. должен устанавливать связь между составляющими.
Все это приводит к необходимости рассмотрения условных законов распределения.
Определение. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина приняла определенное значение, называется условным законом распределения.
Условный закон распределения можно задавать как функцией распределения так и плотностью распределения.
Условная плотность распределения вычисляется по формулам:
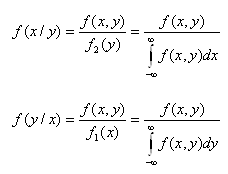
Условная плотность распределения обладает всеми свойствами плотности распределения одной случайной величины.
Условное математическое ожидание.
Определение. Условным математическим ожиданием дискретной случайной величины Y при X = x (х – определенное возможное значение Х) называется произведение всех возможных значений Y на их условные вероятности.
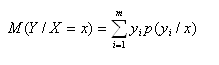
Для непрерывных случайных величин:
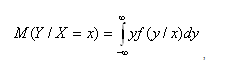
где f(y/x) – условная плотность случайной величины Y при X=x.
3. Функцией регрессии. Линейная регрессия
Условное математическое ожидание M(Y/x)=f(x) является функцией от х и называется функцией регрессии Х на Y.
Пример. Найти условное математическое ожидание составляющей Y при
X= x1=1 для дискретной двумерной случайной величины, заданной таблицей:
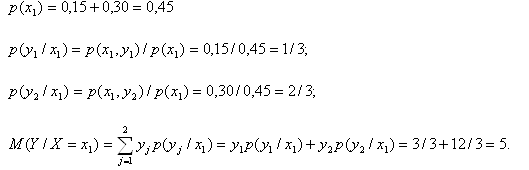
Одной из важнейших форм создания материальной заинтересованности работников в результатах их труда является заработная плата. В. И. Ленин учил, что социализм строить необходимо ... не на энтузиазме непосредственно, а при помощи энтузиазма, рожденного великой революцией, на личном интересе, на личной заинтересованности . Заработная плата служит орудием осуществления экономического закона распределения по труду. Повышение ее наряду с расширением общественных фондов потребления обеспечивает рост благосостояния рабочих и служащих. Именно она должна быть основным источником роста доходов населения.
Экономический закон распределения по труду выражается в том, что труд оплачивается по его качеству и количеству. Качество труда определяется квалификацией рабочего, количество — его выработкой. Для оплаты труда по качеству служит тарифная система, по количеству — системы оплаты, связывающие заработок рабочего с объемом выполненной им работы. Системы оплаты. Заработная плата представляет собой мощную движущую силу роста производительности труда только в том случае, если отвечает требованиям экономического закона распределения по труду.
Вероятностно-статистические модели воспроизводят как устойчивые, так и временные зависимости между экономическими явлениями и факторами. Они позволяют обрабатывать статистические данные и исследовать законы распределения случайных экономических показателей.
Закон неуклонного роста производительности общественного
труда и закон распределения по труду реализуется в планировании производительности труда, установлении пропорций в распределении и использовании трудовых ресурсов, планировании фондов оплаты труда, общественных фондов потребления. [2, c.130]
Принцип материальной заинтересованности заключается в том, что на основе действующего при социализме экономического закона распределения по труду в зависимости от количества и качества его, на предприятиях кроме различных форм оплаты труда и премирования за счет фонда заработной платы образуются фонды материального поощрения и другие специальные фонды в сочетании с материальной ответственностью работников, предусмотренной в действующем хозяйственном и трудовом законодательстве.
График
Формула, описывающая нормальный закон распределения случайной величины, имеет следующий вид:
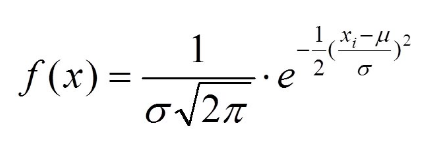
где: μ — генеральное среднее арифметическое; σ — генеральное стандартное отклонение, е — основание натуральных логарифмов, приблизительно равное 2,719, π — число, приблизительно равное 3,142; xi — конкретное значение признака.
Пусть Вас не пугает эта формула. Сейчас мы с ней разберемся. Для начала давайте посмотрим, как выглядит график, построенный на основе этой формулы. Зададим значения μ=0 и σ=1. Хочу заметить, что μ и σ — это просто числа. Их еще называют параметрами распределения. Поэтому критерии, в формулу расчета которых входят параметры распределения называют параметрическими. Например, параметрическим критерием является t-критерий Стьюдента. В формулу расчета критерия Стьюдента входят параметры μ и σ. Кривая нормального распределения вероятностей имеет вид (рис.1).

Рис.1 - График плотности вероятностей нормального распределения при μ=0 и σ=1.
Если мы поменяем параметры, то получим следующее. Изменение параметра μ будет сдвигать график вдоль оси Х. Например при μ=3 график сместится вправо вдоль оси Х (рис.2).

Рис.2 - График плотности вероятностей нормального распределения при μ=3 и σ=1.
Если оставим μ=0, а изменим параметр σ, например σ=3, то получим распределение с большим размахом (рис.3).

Рис.3 - График плотности вероятностей нормального распределения при μ=0 и σ=3.
Свойства нормального распределения
Нормальная кривая имеет колокообразную форму, симметричную относительно точки x=µ, с точками перегиба, абсциссы которых отстоят от µ на ± σ.
Нормальное распределение полностью определятся двумя параметрами: значением генерального среднего (µ) и генерального стандартного отклонения (σ).
Медиана и мода нормального распределения совпадают и равны µ.
Коэффициенты асимметрии и эксцесса нормального распределения равны нулю.
Нормированное отклонение
В области математической статистики важное место занимает нормированное отклонение (t) – показатель, представляющий отклонение той или иной варианты от средней величины, отнесенное к значению стандартного отклонения. Нормированное отклонение рассчитывает по формуле:
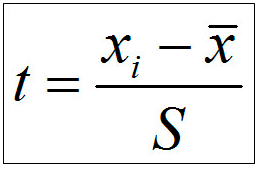
Нормированное отклонение позволяет установить, на сколько «сигм» отклоняются варианты от среднего значения. Например, необходимо определить насколько «сигм» отклоняется значение роста человека, равное 180 см от среднего, если среднее арифметическое равно 170 см, а «сигма», то есть стандартное отклонение равно 10 см. Подставив эти значения в формулу, получим: t= (180-170)/10 = 1.
Ответ: значение роста человека, равное 180 см отклоняется от среднего на одну «сигму».
Нормированное нормальное распределение

Рис.4 - Нормированное нормальное распределение роста мужчин с параметрами: µ=0; σ = 1.
Формула нормального распределения описывает целое семейство кривых, зависящих от двух параметров μ и σ, которые могут принимать любые значения. Поэтому возможно бесконечно много нормально распределенных совокупностей.
Чтобы избежать неудобств, связанных с расчетами для каждого конкретного случая в до компьютерную эпоху было предложено использовать нормированное (стандартное) нормальное распределение, для которого были составлены подробные таблицы. Нормированное нормальное распределение имеет параметры: µ=0; σ = 1 (рис.1, 5). Это распределение получается, если пронормировать нормально распределенную величину Х по формуле:
U= (X-μ)/σ.
Для нормированного нормального распределения характерно, что в интервал µ± σ попадают 68 % всех результатов, в интервал µ± 2σ попадают 95% всех результатов, в интервал µ± 3σ попадают 99 % всех результатов.
В области физической культуры и спорта эти закономерности используют для разработки системы оценок. Так, В.М.Зациорским (рис. 5) предложено использовать следующую систему оценок результатов. Если результат, показанный спортсменом, попал в интервал от -2σ до -1σ — он получает низкую оценку (Рассчитать, в какой интервал попадает результат можно при помощи нормированного отклонения. Это описано выше). Если результат попал в интервал от -1σ до -0,5σ — оценка ниже средней. Средний результат соответствует интервалу от -0,5σ до -0,5σ, результат, получивший оценку выше среднего — от 0,5 до 1σ. Высокий результат попадает в интервал от 1σ до 2σ.

Рис.5 - Анализ
Свойства распределения
Чтобы проверить, соответствует ли распределение нормальному закону, существует много методов.
Можно использовать свойства нормального распределения (равенство среднего, моды и медианы).
Однако более точные результаты дают критерии согласия. В зависимости от объема выборки (n) следует использовать различные критерии:
-
если объем выборки небольшой (n = 10) – критерий Шапиро – Уилки; -
если объем выборки более 40 — критерий хи-квадрат и критерий Колмогорова-Смирнова. -
в статистическом пакете Statgraphics Centurion существует специальная опция — критерии проверки нормальности распределения. В этой опции есть 4 критерия, посредством которых можно сделать вывод о соответствии эмпирического распределения нормальному закону.
Числовые характеристики
Условные законы распределения.
Как было показано выше, зная совместный закон распределения можно легко найти законы распределения каждой случайной величины, входящей в систему.
Однако, на практике чаще стоит обратная задача – по известным законам распределения случайных величин найти их совместный закон распределения.
В общем случае эта задача является неразрешимой, т.к. закон распределения случайной величины ничего не говорит о связи этой величины с другими случайными величинами.
Кроме того, если случайные величины зависимы между собой, то закон распределения не может быть выражен через законы распределения составляющих, т.к. должен устанавливать связь между составляющими.
Все это приводит к необходимости рассмотрения условных законов распределения.
Определение. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина приняла определенное значение, называется условным законом распределения.
Условный закон распределения можно задавать как функцией распределения так и плотностью распределения.
Условная плотность распределения вычисляется по формулам:
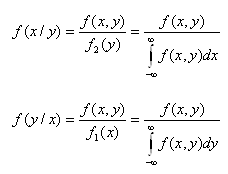
Условная плотность распределения обладает всеми свойствами плотности распределения одной случайной величины.
Условное математическое ожидание.
Определение. Условным математическим ожиданием дискретной случайной величины Y при X = x (х – определенное возможное значение Х) называется произведение всех возможных значений Y на их условные вероятности.
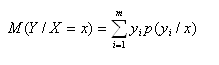
Для непрерывных случайных величин:
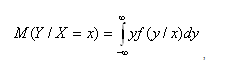
где f(y/x) – условная плотность случайной величины Y при X=x.
3. Функцией регрессии. Линейная регрессия
Условное математическое ожидание M(Y/x)=f(x) является функцией от х и называется функцией регрессии Х на Y.
Пример. Найти условное математическое ожидание составляющей Y при
X= x1=1 для дискретной двумерной случайной величины, заданной таблицей:
| Y | X | |||
| x1=1 | x2=3 | x3=4 | x4=8 | |
| y1=3 | 0,15 | 0,06 | 0,25 | 0,04 |
| y2=6 | 0,30 | 0,10 | 0,03 | 0,07 |