ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
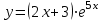.1) Область определения функции:
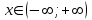,точек разрыва нет. 2)
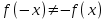и 
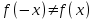, то функция является ни четной и нечетной, график данной функции имеет общий характер,функция непериодическая.4) Найдем точки экстремума и интервалы монотонности
Для этого найдем первую производную от заданной функции и приравняем ее к нулю.
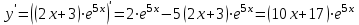
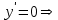
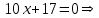
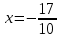.Снесем данные в таблицу:
 |  |  |  |
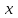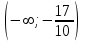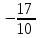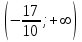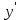 | - | 0 | + |
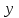 | убывает | 1 | возрастает |
При
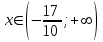- возрастает. При 
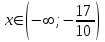- убывает. 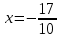- точка минимума.5) Найдем точки перегиба и интервалы выпуклости и вогнутости.
Для этого найдем вторую производную от заданной функции и приравняем ее к нулю
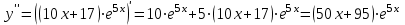
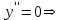
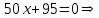
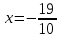. запишем данные в таблицу:
 |  |  |  |
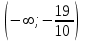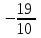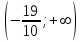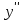 | - | 0 | + |
 | выпуклый | | вогнутый |
При
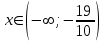график функции выпуклый, при 
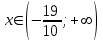- график функции вогнутый. 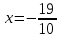- точка перегиба.Найдем наклонные асимптоты
Исследуем при
.
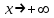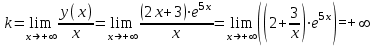
При
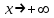горизонтальных и наклонных асимптот нет.Исследуем при
.
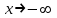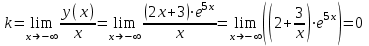
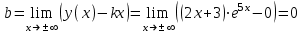
Следовательно, при
, 
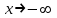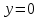- горизонтальная асимптота, наклонных асимптот нет.Найдем точки пересечения с координатными осями:
.
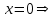
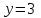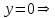
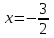.Построим график
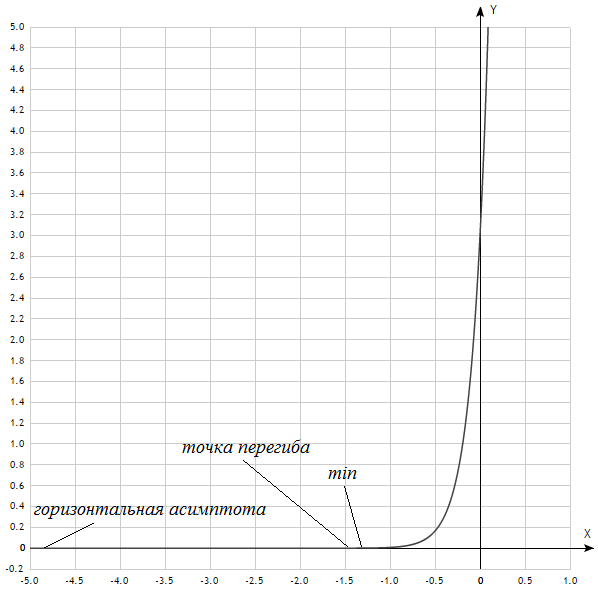
6)Используя свойства определенного интеграла, искомая площадь будет равна:
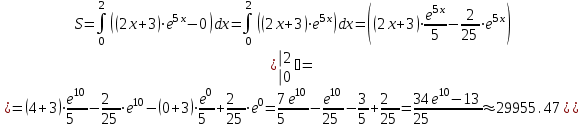(условных квадратных единиц).Таблица
| Область определения: |  |
| Четность, периодичность: | Функция является ни четной и нечетной, не периодичная |
| Поведение на концах области определения: | При  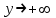 При   |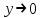
| Асимптоты: |  - горизонтальная асимптота |
| Промежутки монотонности: | При  график функции выпуклый, при  - график функции вогнутый. |
| Точки экстремума: |  - точка минимума |
| Промежутки выпуклости: | При график функции выпуклый, при - график функции вогнутый. |
| Точки перегиба: |  - точка перегиба |
| Площадь криволинейной трапеции: | 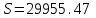 условных квадратных единиц. |