Добавлен: 09.01.2024
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
Пермский национальный исследовательский политехнический университет
Кафедра «Авиационные двигатели»
Дисциплина: «Конструкция и проектирование авиационных двигателей и энергетических установок»
Отчет к лабораторной работе №3
Тема: Расчетный анализ колебаний рабочих лопаток ГТД
Вариант № 19
Выполнили студенты гр. АД-18-1с
Каткова Е.А.
Конюшевская К.В.
Работа принята ____________________
2023
-
Методика определения низшей собственной частоты колебаний рабочих лопаток.
Для расчета низшей собственной частоты невращающейся лопатки используется закон Рэлея.
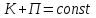 .
.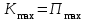 ,
, 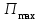 – в момент максимального отклонения.
– в момент максимального отклонения.Рассматриваем гармонические колебания с круговой собственной частотой p. В качестве допущений принимаются: стержневая модель, жёсткое консольное закрепление, отсутствие потерь энергии, а также рассматриваются свободные гармонические колебания по первой изгибной форме.
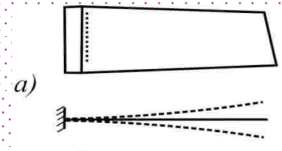
Рисунок 1 – Первая изгибная собственная форма колебаний лопатки
Перемещения произвольной точки оси лопатки с координатой x задают в виде:
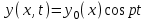 .
.Максимальная кинетическая энергия:
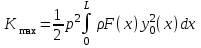 .
.Максимальная потенциальная энергия:
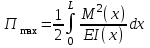
,
где
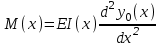 – изгибающий момент, соответствующий прогибу
– изгибающий момент, соответствующий прогибу 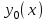 .
.Отсюда, круговая собственная частота:
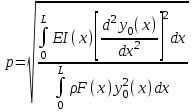 .
.Собственная частота колебаний лопатки при комнатной температуре без учёта вращения:
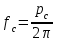 .
.Изменение собственной частоты колебаний лопатки с учетом вращения и изменения температуры:
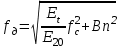 ,
,где
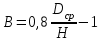 – коэффициент динамического ужесточения.
– коэффициент динамического ужесточения.-
Подготовка исходных данных для анализа колебаний лопатки. Расчет низшей собственной частоты колебаний лопатки.
Для заданного варианта лопатки была построена таблица с исходными данными, таблица с геометрическими параметрами пяти расчётных сечений лопатки, а также таблица с характеристиками материала лопатки. Помимо этого, было вычислено значение низшей собственной частоты колебаний. Параметры материала были найдены исходя из прил. Е. [1]
| Вариант | № ступени | Узел | Частота вращения ротора минимальная 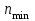 , об/мин , об/мин | Частота вращения ротора максимальная 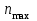 , об/мин , об/мин | Число направляющих лопаток перед рабочим колесом z1 | Число направляющих лопаток за рабочим колесом z2 | Температура лопатки 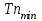 при при 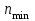 , К , К | Температура лопатки 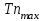 при при 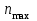 , К , К |
| 19 | 7 | КВД | 7200 | 11600 | 85 | 85 | 380 | 610 |
Таблица 1 – Исходные данные для расчёта
Таблица 2 – Геометрические параметры пяти расчётных сечений лопатки
| N | R, мм | Cmax, мм | h, мм | b, мм | β, ° |
| V-V | 280,5 | 1,74 | 1,38 | 25 | 36° |
| IV-IV | 270,75 | 1,94 | 1,405 | 25 | 32°40` |
| III-III | 261 | 2,125 | 1,605 | 25 | 28°25` |
| II-II | 251,25 | 2,317 | 1,86 | 25 | 24°10` |
| I-I | 241,5 | 2,52 | 2,27 | 25 | 19°40` |
Таблица 3 – Характеристики материала лопатки
| р, кг/м3 | Сигма пред, МПа | E20, 1*1011Па |
| 4500 | 720 | 1,165 |
Вычисленное значение низшей собственной частоты колебаний:
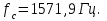
-
Построение резонансной диаграммы. Анализ возможных резонансных режимов лопатки.
Характер изменения температуры лопатки принимается в соответствии с рисунком 2, приведенным ниже. Зависимость была построена с помощью исходных данных. Также в таблице 4 приведены результаты вычисления динамической собственной частоты для 11 значений частоты вращения ротора, а на рисунке 3 – резонансная диаграмма.
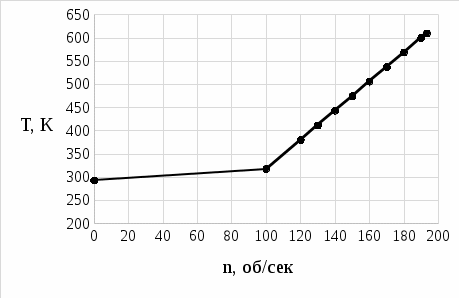
Рисунок 2 – Зависимость температуры лопатки от частоты вращения
Таблица 4 – Результаты вычисления динамической собственной частоты
| n, об/сек | T, К | Et, 1*1011Па | 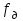 ,Гц ,Гц |
| 0 | 293 | 1,165 | 1571,913 |
| 100 | 317,62 | 1,165 | 1602,494 |
| 120 | 380 | 1,16 | 1612,481 |
| 130 | 411,82 | 1,156 | 1617,369 |
| 140 | 443,22 | 1,15 | 1621,532 |
| 150 | 474,62 | 1,146 | 1627,586 |
| 160 | 506,02 | 1,14 | 1632,913 |
| 170 | 537,42 | 1,133 | 1638,167 |
| 180 | 568,82 | 1,125 | 1643,351 |
| 190 | 600,22 | 1,12 | 1651,035 |
| 193,3333 | 610 | 1,12 | 1654,787 |
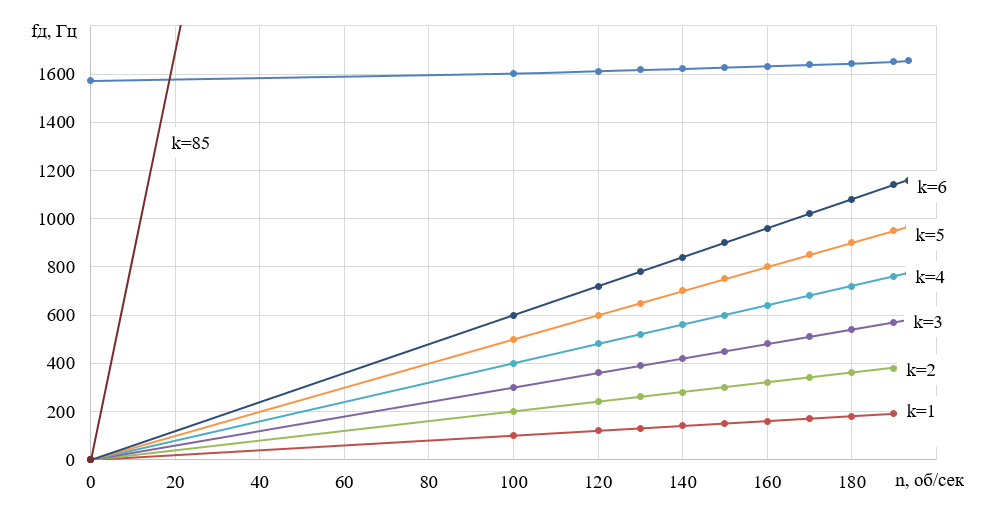
Рисунок 3 – Резонансная диаграмма
Резонанс наступает при совпадении частоты одной из гармонических составляющих нагрузки kn с любой из собственных динамических частот
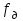 . Исходя из рисунка 3 можно заметить, что резонанс может наступить при совпадении частоты 85 гармоники нагрузки с динамической собственной частотой. Однако интервал рабочей частоты вращения ротора составляет от 120 до 193,33 об/сек, а резонансный режим наступает на частоте менее 20 об/сек. Это означает, что лопатка будет работать в резонансном режиме незначительное количество времени, и мероприятия по отстройке от резонанса не требуются.
. Исходя из рисунка 3 можно заметить, что резонанс может наступить при совпадении частоты 85 гармоники нагрузки с динамической собственной частотой. Однако интервал рабочей частоты вращения ротора составляет от 120 до 193,33 об/сек, а резонансный режим наступает на частоте менее 20 об/сек. Это означает, что лопатка будет работать в резонансном режиме незначительное количество времени, и мероприятия по отстройке от резонанса не требуются.
4. Анализ влияния конструктивных факторов на низшую собственную частоту колебаний рабочей лопатки.
4.1. Оценка влияния максимальной толщины профиля на собственную частоту колебаний лопатки.
При увеличении максимальной толщины профиля лопатки на 10 %.
Таблица 5 – Измененные геометрические параметры лопатки
| N | R, мм | Cmax, мм | Cmax изм, мм |
| V-V | 280,5 | 1,74 | 1,827 |
| IV-IV | 270,75 | 1,94 | 2,037 |
| III-III | 261 | 2,125 | 2,23 |
| II-II | 251,25 | 2,317 | 2,43 |
| I-I | 241,5 | 2,52 | 2,646 |
Измененная собственная частота:
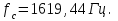
Низшая собственная частота немного повысилась. Это произошло из-за того, что собственная частота пропорциональна толщине профиля:
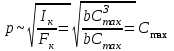 .
.Динамические собственные частоты также оказались приближенно пропорциональны толщине профиля. Таким образом с помощью изменения толщины профиля лопатки можно было бы произвести отстройку от резонанса.
4.2 Оценка влияния кривизны профиля на собственную частоту колебаний лопатки.
При увеличении кривизны профиля на 5%.
Таблица 6 – Измененные геометрические параметры лопатки
| N | R, мм | h, мм | hизм, мм |
| V-V | 280,5 | 1,38 | 1,518 |
| IV-IV | 270,75 | 1,405 | 1,545 |
| III-III | 261 | 1,605 | 1,765 |
| II-II | 251,25 | 1,86 | 2,046 |
| I-I | 241,5 | 2,27 | 2,497 |