ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ



МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»

Кафедра общей и технической физики

МЕХАНИКА

ЛАБОРАТОРНАЯ РАБОТА №3

«Определение ускорения свободного падения при помощи универсального маятника»

По дисциплине Физика

(наименование учебной дисциплины, согласно учебному плану)

Выполнил: студент гр. НБШ-22 Самбурский А.М.

(шифр группы) (подпись) (Ф.И.О.)

Дата:

Проверил

руководитель работы:

(должность) (подпись) (Ф.И.О.)

Санкт-Петербург

2023

Цель работы

Определить ускорение свободного падения при помощи универсального маятника.

Краткое теоретическое содержание

Явление, изучаемое в работе. Колебания маятника под действием силы тяжести.

Определения основных физических понятий, объектов, процессов и величин.

Ускорение свободного падения — ускорение, придаваемое телу силой тяжести, при исключении из рассмотрения других сил.

Колебание —повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.

Период — минимальное время, за которое совершается одно полное колебательное движение.

Приведённая длина физического маятника — длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

---

Математический маятник — материальная точка, подвешенная на невесомой, нерастяжимой нити и совершающая колебание в вертикальной плоскости под действием силы тяжести.

Физический маятник — абсолютно твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр тяжести.

Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении.

Законы и соотношения, описывающие изучаемые процессы, на основании которых, получены расчётные формулы. Пояснения к физическим величинам и их единицы измерений.

Теорема Штейнера — момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.



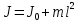
Где 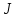— момент инерции относительно произвольной оси, ;

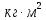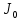— момент инерции относительно оси, параллельной произвольной и проходящей через центр масс тела, ;

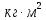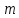— масса тела, ;

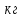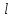— расстояние между осями, .

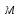Основные расчетные формулы.

Ускорение свободного падения, рассчитанное при помощи математического маятника, :



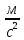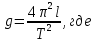
g — ускорение свободного падения,

---

;

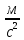
l— длина математического маятника, м;

T— период колебаний, c.
Ускорение свободного падения, рассчитанное при помощи оборотного маятника, :



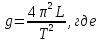
g — ускорение свободного падения, ;

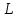— приведённая длина оборотного маятника, м;

T— период колебаний, c.
Период колебаний, с:



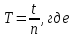
T— период колебаний, c;

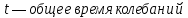с;

.

Формулы для расчёта погрешностей косвенных измерений.

= ; =

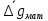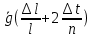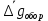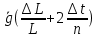
Где 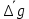— максимальная абсолютная погрешность ускорения свободного падения,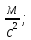

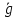— среднее значение ускорение свободного падения,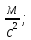

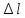— погрешность измерения длины математического маятника, м;

— длина математического маятника, м;

∆T— погрешность периода, с;

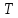— период колебаний, с;

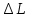— погрешность измерения приведённой длины оборотного маятника, м;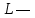

---

приведённая длина оборотного маятника, м.

Таблицы.

Таблица 1. Математический маятник

Величина	t	T	g
Единицы измерения	c	c
1	14,333	1,4333	9,993
2	14,332	1,4332	9,994
3	14,331	1,4331	9,996
4	14,33	1,433	9,997
5	14,334	1,4334	9,991
6	14,335	1,4335	9,99
7	14,327	1,4327	10,001
8	14,329	1,4329	9,998
9	14,33	1,433	9,997
10	14,33	1,433	9,997

Таблица 2. Оборотный маятник

Величина	t	T	g
Единицы измерения	c	c
С1	12,574	1,2574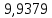
С2	12,578	1,2578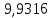

Пример вычислений.

Исходные данные:

L= 39,8 cм = 0,398 м

l = 52 см = 0,52 м

n = 10

Погрешности прямых измерений:

1. 
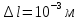   (погрешность измерения длины математического маятника)
   
2. 
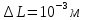   (погрешность измерения приведённой длины оборотного маятника)
   
3. 
   ∆t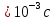 (погрешность измерения времени)
   

---

Вычисления:

Математический маятник.

Пример вычисления для таблицы 1, опыта №1:





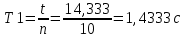
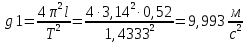
Среднее значение величины ускорения свободного падения:



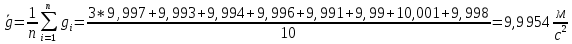
Абсолютная погрешность для величины ускорения свободного падения:

=
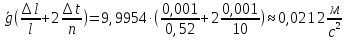
Оборотный маятник.

Пример вычисления для таблицы 2, опыта №1:





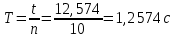
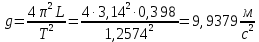
Среднее значение величины ускорения свободного падения:



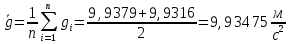
Абсолютная погрешность для величины ускорения свободного падения:

=
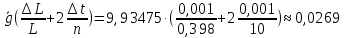
Результат.

Ускорение свободного падения при измерении математическим и оборотным маятниками с учётом максимальной абсолютной ошибки:




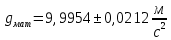
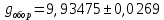
Сравнительная оценка результатов.

Справочное значение ускорения свободного падения — 9,81 .

Расхождение теоретического и экспериментального значений:

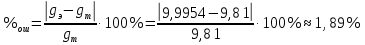- измерение с помощью математического маятника.

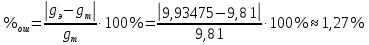- измерение с помощью физического маятника.
Вывод.

В ходе данной лабораторной работы была рассчитана величина ускорения свободного падения. Для получения необходимых данных были использованы математический и оборотный маятники. Показатель, измеренный математическим маятником, расходится с теоретическим значением на 1,89%. Показатель, измеренный оборотным маятником, разошелся с теоретическим значением на 1,27%. При измерении ускорения свободного падения с помощью физического маятника, мне нужно было добиться того, чтобы периоды равнялись друг другу. Периоды измерений математического маятника отличаются друг от друга всего лишь на 0,06%, оборотного маятника ̶ на 0,03%, что является более чем допустимыми результами. Цель работы была достигнута, а полученные измерения являются крайне приближёнными к теоретическому значению.

---

Смотрите также файлы

• И. М. Губкина Факультет Кафедра Направление (специальность) Программа.docx

• Презентацияпроекта образовательный центр иностранного языка.ppt

• Среднее 10,2.docx

• Задача Создатель ЮтубКанала Бешенство фемки.docx

• Курсовая работа по дисциплинам Экономика организации.docx