Файл: Методические указания по проведению практических занятий по метрологии и измерительной технике для студентов всех специальностей очной формы обучения.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 250
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
I3 и возможные пределы его действительного значения, оцените точность измерения тока I3, если при измерениях получены следующие значения токов:
I1 = 17,5А с абсолютной погрешностью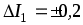 А; I2 = 7,5А с абсолютной погрешностью
А; I2 = 7,5А с абсолютной погрешностью 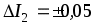 А.
А.
Решение:
1. Ток I3, определенный по показаниям приборов без учета их погрешностей
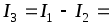 17,5 7,5 = 10(А).
17,5 7,5 = 10(А).
2. Наибольшая абсолютная погрешность измерения тока I3 равна сумме модулей абсолютных погрешностей измерения токов I1 и I2, т. е.
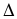 I3 max
I3 max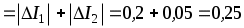 (А).
(А).
Следовательно, наибольшая относительная погрешность измерения тока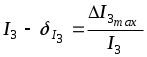 и равна:
и равна:
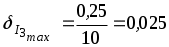 (или 2,5%).
(или 2,5%).
3. Возможное действительное значение тока I3 будет находиться в пределах границ от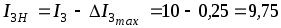 (А), до
(А), до 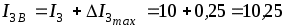 (А).
(А).
4. Точность измерения, согласно определению, есть величина, обратная относительной погрешности. Следовательно, точность измерения тока I3 в данном эксперименте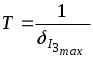 и равна:
и равна:
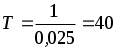 .
.
Ответ: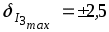 %; 9,75А
%; 9,75А 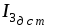 10,25А; точность измерения
10,25А; точность измерения 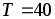 .
.
2.2.3. Задачи для самостоятельного решения
1. Амперметр с пределом измерения 10А показал при измерениях ток 5,3А, при его действительном значении 5,23А. Определите абсолютную, относительную и относительную приведенную погрешности.
2. Погрешность эксплуатируемых счетчиков электрической энергии в среднем 2%. К какой неопределенности в учете энергии (в абсолютных цифрах) приводит этот уровень точности счетчиков, если в стране вырабатывается 1600 млрд. кВтч за год? (для справки, средняя годовая выработка Волжской ГЭС 11 млрд. кВтч).
3. Определите абсолютную погрешность атомных часов, использующих колебание молекул газа на частоте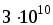 Гц, за год, если относительная погрешность составляет
Гц, за год, если относительная погрешность составляет 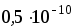 .
.
4. Имеются следующие результаты измерений: (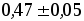 ) мм; (
) мм; (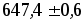 ) мм и (
) мм и (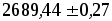 ) мм.
) мм.
Сравните эти результаты по точности. Какой из них самый точный? Во сколько раз точность лучшего результата больше самого грубого?
5. Оцените относительную погрешность самых распространенных измерительных приборов простых бытовых часов, с суточным ходом в 20 сек. (суточный ход поправка к показаниям часов за сутки).
2.3. Систематические погрешности
2.3.1. Вопросы для самоконтроля
1) Перечислите источники систематических погрешностей. Приведите классификацию их по причине возникновения.
2) Дайте определение понятию “методическая погрешность”, поясните причины появления и особенности методических погрешностей.
3) Дайте определение понятию “инструментальная погрешность”, перечислите разновидности их, поясните причины появления и особенности.
4) Поясните причины появления и особенности “личных” погрешностей.
5) Объясните, почему часть инструментальных погрешностей выделяют в отдельную группу и называют погрешности “обусловленные отклонением внешних условий”? Для чего это делается?
6) Дайте определение понятиям “неисправленный результат”, “исправленный результат”, “поправка”.
7) Дайте определение понятию “неисключенный остаток систематичекой погрешности” (НСП), поясните причины появления НСП.
8) Назовите известные вам способы устранения систематической погрешности в процессе измерения.
9) Приведите примеры, поясняющие устранение систематической погрешности методом замещения и методом противопоставления.
10) Приведите пример, поясняющий устранение систематической погрешности в процессе измерения с использованием способа компенсации ее по знаку.
2.3.2. Примеры решения задач
Задача № 2.3
При измерении напряжения показания вольтметра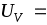 21,5 В. Поправка к показаниям прибора
21,5 В. Поправка к показаниям прибора 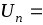 +0,1 В. Определите значение погрешности измерения и погрешности средства измерений (вольтметра), если действительное значение напряжения Uдст = 21,55 В.
+0,1 В. Определите значение погрешности измерения и погрешности средства измерений (вольтметра), если действительное значение напряжения Uдст = 21,55 В.
Решение:
1. По условиям задачи показания вольтметра это неисправленный результат измерения, т. е.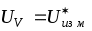 , следовательно, погрешность средства измерений (вольтметра) будет определяться следующим образом:
, следовательно, погрешность средства измерений (вольтметра) будет определяться следующим образом:
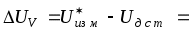
21,5 21,55 = 0,05 (В).
2. Результатом измерения напряжения будет исправленный результат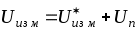 , т. е.
, т. е.
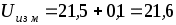 (В).
(В).
3. Погрешность измерения (по определению)
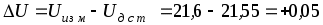 (В).
(В).
Ответ: погрешность СИ -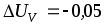 В;
В;
погрешность измерения -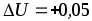 В.
В.
Задача № 2.4
Сопротивление RX измеряется с помощью равноплечего моста, в котором номинальные значения резисторов R2 и R3 равны по 1000 Ом.
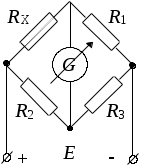
Равновесие моста достигается тогда, когда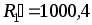 Ом. При измерении RX мостовым методом имеет место систематическая погрешность, обусловленная тем, что реальные значения резисторов R2 и R3 несколько отличаются от номинальных значений и фактически всегда R2 ≠ R3 . Для устранения этой погрешности измерения производят дважды: первый раз так, как показано на рисунке, а второй раз – поменяв местами резисторы RX и R1 в плечах моста. За результат принимают среднее значение из двух измерений. После перемены местами RX и R1 (для устранения систематической погрешности), равновесие достигается при
Ом. При измерении RX мостовым методом имеет место систематическая погрешность, обусловленная тем, что реальные значения резисторов R2 и R3 несколько отличаются от номинальных значений и фактически всегда R2 ≠ R3 . Для устранения этой погрешности измерения производят дважды: первый раз так, как показано на рисунке, а второй раз – поменяв местами резисторы RX и R1 в плечах моста. За результат принимают среднее значение из двух измерений. После перемены местами RX и R1 (для устранения систематической погрешности), равновесие достигается при 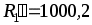 Ом. Составьте уравнение измерения RX, определите его значение и действительное соотношение плеч моста
Ом. Составьте уравнение измерения RX, определите его значение и действительное соотношение плеч моста 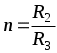 . Классифицируйте метод измерения RX и метод устранения систематической погрешности.
. Классифицируйте метод измерения RX и метод устранения систематической погрешности.
Решение:
1. Условие равновесия моста записывается в следующем виде:
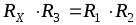 , откуда
, откуда 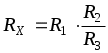
и в идеале, при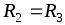 ,
, 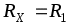 . Из-за неточного равенства
. Из-за неточного равенства 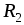 и
и 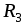 условие равновесия моста в первом и втором случаях следует записать:
условие равновесия моста в первом и втором случаях следует записать:
1.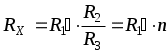 , где
, где  ;
;
2.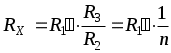 .
.
Пусть, например,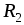 немного меньше
немного меньше 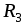 (п 1), тогда в первом случае R'1 будет немного больше действительного значения RX , то есть R'1= =RX+ΔRXст ,а во втором случае R''1 на такую же величину меньше, то есть R''1= RX –ΔRXст. Следовательно, значение сопротивления
(п 1), тогда в первом случае R'1 будет немного больше действительного значения RX , то есть R'1= =RX+ΔRXст ,а во втором случае R''1 на такую же величину меньше, то есть R''1= RX –ΔRXст. Следовательно, значение сопротивления 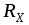 может быть найдено по результатам двух измерений следующим образом:
может быть найдено по результатам двух измерений следующим образом:
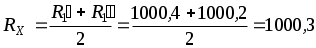 (Ом).
(Ом).
2. Действительное соотношение резисторов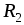 и
и 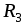 (
(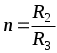 ) можем найти, например, решая совместно уравнения баланса моста в первом и втором случаях;
) можем найти, например, решая совместно уравнения баланса моста в первом и втором случаях;
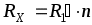 и
и 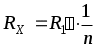 ,
,
откуда получаем:
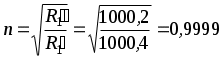 .
.
3. При измерении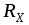 одинарным мостом реализуется метод сравнения. Неизвестное сопротивление
одинарным мостом реализуется метод сравнения. Неизвестное сопротивление 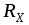
I1 = 17,5А с абсолютной погрешностью
Решение:
1. Ток I3, определенный по показаниям приборов без учета их погрешностей
2. Наибольшая абсолютная погрешность измерения тока I3 равна сумме модулей абсолютных погрешностей измерения токов I1 и I2, т. е.
Следовательно, наибольшая относительная погрешность измерения тока
3. Возможное действительное значение тока I3 будет находиться в пределах границ от
4. Точность измерения, согласно определению, есть величина, обратная относительной погрешности. Следовательно, точность измерения тока I3 в данном эксперименте
Ответ:
2.2.3. Задачи для самостоятельного решения
1. Амперметр с пределом измерения 10А показал при измерениях ток 5,3А, при его действительном значении 5,23А. Определите абсолютную, относительную и относительную приведенную погрешности.
2. Погрешность эксплуатируемых счетчиков электрической энергии в среднем 2%. К какой неопределенности в учете энергии (в абсолютных цифрах) приводит этот уровень точности счетчиков, если в стране вырабатывается 1600 млрд. кВтч за год? (для справки, средняя годовая выработка Волжской ГЭС 11 млрд. кВтч).
3. Определите абсолютную погрешность атомных часов, использующих колебание молекул газа на частоте
4. Имеются следующие результаты измерений: (
Сравните эти результаты по точности. Какой из них самый точный? Во сколько раз точность лучшего результата больше самого грубого?
5. Оцените относительную погрешность самых распространенных измерительных приборов простых бытовых часов, с суточным ходом в 20 сек. (суточный ход поправка к показаниям часов за сутки).
2.3. Систематические погрешности
2.3.1. Вопросы для самоконтроля
1) Перечислите источники систематических погрешностей. Приведите классификацию их по причине возникновения.
2) Дайте определение понятию “методическая погрешность”, поясните причины появления и особенности методических погрешностей.
3) Дайте определение понятию “инструментальная погрешность”, перечислите разновидности их, поясните причины появления и особенности.
4) Поясните причины появления и особенности “личных” погрешностей.
5) Объясните, почему часть инструментальных погрешностей выделяют в отдельную группу и называют погрешности “обусловленные отклонением внешних условий”? Для чего это делается?
6) Дайте определение понятиям “неисправленный результат”, “исправленный результат”, “поправка”.
7) Дайте определение понятию “неисключенный остаток систематичекой погрешности” (НСП), поясните причины появления НСП.
8) Назовите известные вам способы устранения систематической погрешности в процессе измерения.
9) Приведите примеры, поясняющие устранение систематической погрешности методом замещения и методом противопоставления.
10) Приведите пример, поясняющий устранение систематической погрешности в процессе измерения с использованием способа компенсации ее по знаку.
2.3.2. Примеры решения задач
Задача № 2.3
При измерении напряжения показания вольтметра
Решение:
1. По условиям задачи показания вольтметра это неисправленный результат измерения, т. е.
21,5 21,55 = 0,05 (В).
2. Результатом измерения напряжения будет исправленный результат
3. Погрешность измерения (по определению)
Ответ: погрешность СИ -
погрешность измерения -
Задача № 2.4
Сопротивление RX измеряется с помощью равноплечего моста, в котором номинальные значения резисторов R2 и R3 равны по 1000 Ом.

Равновесие моста достигается тогда, когда
Решение:
1. Условие равновесия моста записывается в следующем виде:
и в идеале, при
1.
2.
Пусть, например,
2. Действительное соотношение резисторов
откуда получаем:
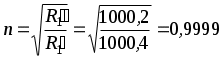 .
.3. При измерении