Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени

федеральное государственное бюджетное образовательное учреждение

высшего образования

«Московский технический университет связи и информатики»

Факультет СиСС

Кафедра «Сети связи и системы коммутации»

Лабораторная работа №1

«Структурные матрицы сетей и операции с ними»

Вариант №10

Выполнил: студент гр. БОС-2002

Ядринцев С.М.

Проверил: к.т.н., доцент Данилов А.Н.

Москва, 2023 г.

1. Цель работы

Изучить и практически освоить описание структурных параметров сетей связи с использованием математического аппарата булевой алгебры. Путем преобразования структурных матриц получить перечень путей, сечений и квазисечений.

2. Задание

2.1. Ознакомиться с основными определениями структурного анализа сетей связи: граф сети, путь, ранг пути, способы записи путей, сечение, квазисечение, правила булевой алгебры.

2.2. Изучить методы получения множества путей и сечений из структурной матрицы.

2.3. Получить задание у преподавателя.

2.4. Согласно полученному варианту задания провести анализ сети:

• записать структурную матрицу сети;

• визуально по схеме графа найти и записать все возможные пути от узла i к узлу j

• определить пути ранга r≤ 3 для заданной пары узлов;

• путем преобразования структурной матрицы найти и записать все пути от узла i к узлу j и все пути ранга r ≤ 3;

• по структурной матрице построить дерево путей с корнем в узле i ранга r≤ 3 для связи с узлом j и сравнить полученный результат с результатами, полученными при выполнении предыдущих пунктов;

• используя аппарат булевой алгебры, найти квазисечения между узлами

iи j для множества путей с рангом

---

r < 3.

Выполнение
Вариант задания

i = 6

j = 2


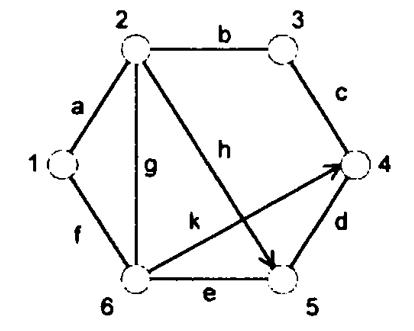
Структурная матрица сети

1		2	3	4	5	6
1	1	a	0	0	0	f
2		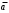1	b	0	h	g
3	0		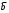1	c	0	0
5	0	0		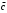1	d	0
5	0	0	0		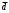1	e
6		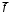	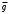0		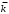	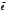1

Множество путей от вершины i = 6 к вершине j = 2 можно записать следующим образом:

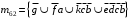
Из m₄₂ можно выделить подмножество тех путей, ранг которых будет, например, не более двух:


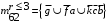
Множество путей проще всего может быть найдено раскрытием минора структурной матрицы В, получаемого путем вычеркивания i-го столбца и j-й строки в матрице В, и последующим разложением полученного определителя по строке.

---

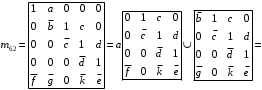
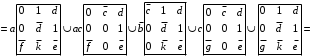
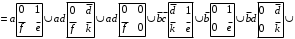
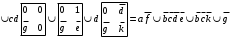
Для построения дерева путей из вершины 1 берем первую строку матрицы В и помечаем на графе вершины путей с r =1, имеющие b_ij ≠ 0. После того как процесс для строки закончен и отмечены номера вершин (по номеру столбца), переходим к строке одного из тех узлов, которые расположены на линии r - 1, и продолжаем процесс аналогичным образом. При этом следует учитывать, что вершины в одном пути не должны повторяться.



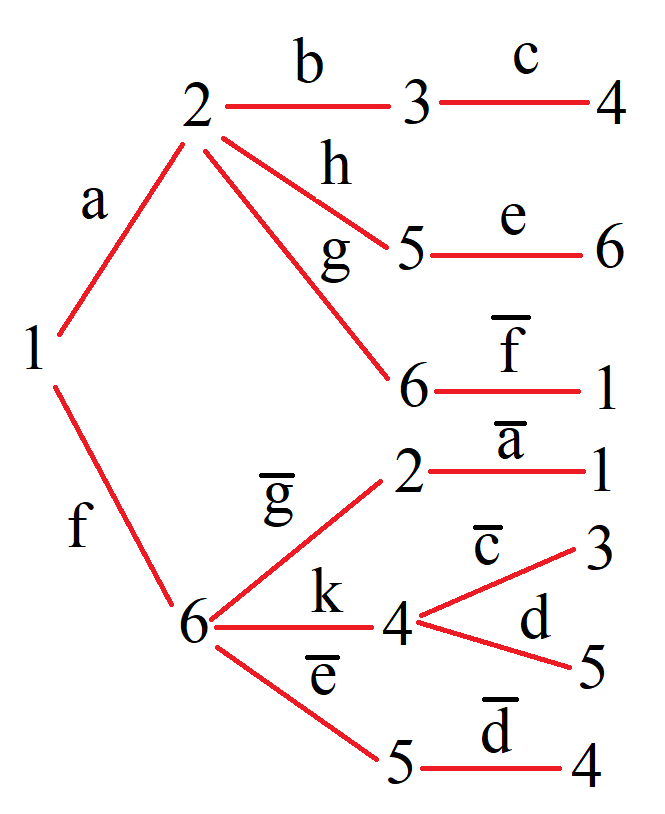
Для нахождения сечений (или квазисечений, т.е. сечений, рассекающих пути только до определенного ранга) следует заменить функцию m₆₂ на двойственную, заменив дизъюнкцию конъюнкцией и, наоборот, - конъюнкцию дизъюнкцией.



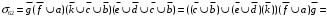
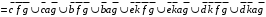
Вывод
Я изучил и практически освоил описание структурных параметров сетей связи с использованием математического аппарата булевой алгебры. Путем преобразования структурных матриц получить перечень путей, сечений и квазисечений.

---

Смотрите также файлы

• Описание сборки дбр 2 (мое видение) Сборка узла корпуса.docx

• Практическая работа 5 Проектирование учебного занятия на основании примерной рабочей программы, умк по английскому языку.docx

• Тест 1 по темам Интеграция отрасли печати в современную медиаиндустрию и Интеграция печатных и электронных изданий.doc

• Правовой акт федерального органа государственной власти.doc

• Название работы Разработка практикумов для работы с исполнителем на уроках информатики в основной школе.docx