ЛАБОРАТОРНОЕ ЗАНЯТИЕ № 15
Обслуживание простейшего потока вызовов полнодоступным пучком с ожиданием при показательном распределении длительности занятия.
Цель работы:  анализ качества обслуживания полнодоступной системы с явными потерями с применением первой формулы Эрланга.

Подготовка к работе

          Изучить и освоить теоретический материал по  первому распределению Эрланга и характеристикам качества обслуживания полнодоступной системой с явными потерями, знать первую формулу Эрланга, рекуррентную форму этой формулы, количественные характеристики качества обслуживания.

Задание к работе

1 Разработать программу на алгоритмическом языке, реализующую рекуррентную форму первой формулы Эрланга

  

 

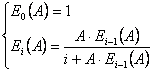
2 Построить график распределения Pi для V-канальной  полнодоступной системы с явными потерями, если на вход поступает простейший поток вызовов с  интенсивностью   λ (Эрл). Число каналов обслуживания V и значение λ определяется по вариантам.

3   Определить характеристики качества обслуживания:

а) вероятность потери вызова Pb( );

б) вероятность потерь по времени Pt( );

в) вероятность потерь по нагрузке Pн( );

г) обслуженную нагрузку Y.

Порядок выполнения работы

1 Получить задание и вариант работы у преподавателя.

2 Разработать алгоритм и программу.

3 Осуществить ввод программы и её отладку.

4 Получить результаты работы программы.

5 График построить в Excel.

6 Сделать выводы и анализ полученных результатов.

7 Подготовить отчет о выполненной работе, где представить алгоритм и листинг программы,  результаты вычислений и анализ полученных данных.

---

Материал для подготовки к лабораторной работе

 Следующая формула

                                                    

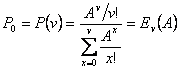
носит название первой формулы Эрланга, в некоторых источниках её называют В – формулой Эрланга.

С помощью данной формулы при известных значениях поступающей нагрузки А и числа линий v можно вычислить вероятность потери поступающего вызова.

Данная формула табулирована. Для вычисления Ev(A) при больших значениях v используют рекуррентную формулу

 

.

 

Итак, с помощью первой формулы Эрланга можно вычислить характеристики качества обслуживания полнодоступной системы с явными потерями, когда на неё поступает простейший поток вызовов. Среди перечисленных ниже характеристик главной является вероятность потери поступившего вызова:

а) вероятность потери по времени

 

                                 Pt = Ev (A);

 

б) вероятность потери вызова

 

                                Pв = Ev (A);

 

в) вероятность потери по нагрузке

 

                                  Pн = Ev (A);

 

г) пропускная способность определяется следующим образом (значение У табулировано)

 

            У = А – Упот = А – А* Ev (A) = А(1 - Ev (A));

 

д) пропускная способность отдельных выходов при случайном занятии

 

                                                                 ,

 

при упорядоченном занятии

                                                 

                                                        .

   

3.6 Варианты лабораторной работы

                               

---

                               Т а б л и ц а 8

 

Номер варианта	V	t   (сек)	λ (выз/мин)
1	5	100	4
2	6	105	5
3	7	110	5,7
4	8	115	6,2
5	9	120	6,7
6	10	125	7
7	11	130	7,3
8	12	135	7,5
9	13	140	7,7
10	7	145	7,8
11	8	150	8
12	9	155	8,1
13	10	160	8,2
14	11	165	8,3
15	12	170	8,4

 

 

Контрольные вопросы.

 1  Привести первую формулу Эрланга.

 2 Какая величина вычисляется с помощью первой формулы Эрланга.

 3 Дать определение характеристикам качества полнодоступной системы обслуживания с явными    потерями.

---

Смотрите также файлы

• Компьютер жне ауіпсіздік.docx

• ысамерзімді жоспар Сабаты таырыбы Заттарды жіктелуі.docx

• Занятие для обучающихся 8 11 классов по теме день защитника отечества.docx

• Подземные машины Шахтные погрузочнотранспортные машины Введение.docx

• Реферат по теме Возможности экономического роста регионов страны. Факторы и типы экономического роста по дисциплине Основы экономики и финансовой грамотности.doc