Файл: Лабораторная работа по общей физике 31. Некоторые законы случайных событий.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 60
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(надстрочной чертой над случайной величиной далее будем отмечать операцию усреднения по совокупности N случайных значений этой величины). 
. При достаточно больших N и Nk относительную частоту 
можно заменить вероятностью P попадания значения X в интервал xk, xk + xk. Тогда среднее значение 
. При достаточно малых xk суммирование можно заменить интегрированием 
(7)Интеграл в равенстве (7) величина не случайная. Она называется математическим ожиданием случайной величины X и обозначается M(X). Вероятность отклонения
от M(X) при увеличении числа испытаний N стремится к нулю. В этом смысле и надо понимать приближенное равенство 
.Для нормального распределения (5) M(X) совпадает с наиболее вероятным значением a, т.е.
.Математическое ожидание является одним из основных параметров, характеризующих распределение вероятности.
Другим важным параметром является дисперсия, она характеризует отклонение случайной величины от среднего значения. Рассмотрим квадрат отклонения случайной величины от среднего значения (x –
)2. Из расчета, аналогичного тому, который привел к выражению (7), получается 
. (8)Правая часть последнего равенства не случайная величина, обозначим ее D. Среднее значение квадрата отклонения случайной величины от своего среднего приблизительно равна D. Приблизительность равенства имеет тот смысл, что при большом числе испытаний редки будут заметные отклонения
от D. Величина D называется дисперсией случайной величины. Величина 
называется стандартом.
Для нормального закона (5) интеграл (8) равен 2, т.е. D = 2. Таким образом, величина – это стандарт случайной величины, подчиняющийся нормальному закону, или среднеквадратичное ее отклонение от среднего значения.
Задание 1.
Проследите несколько раз за движением отдельной частицы по доске Гальтона. Зарисуйте приблизительно траектории частиц.
Задание 2.
Выполните три серии испытаний с разными числами N, равными N = 10, N = N0/2 (половина стакана), N = N0. Для каждой серии произведите не менее трех опытов. Результаты опытов зафиксируйте следующим образом. При N = 10 запишите в Таблицу 1 номера ячеек, в которые попали частицы, и количество частиц в ячейке:
Таблица 1.
| Номер ячейки | | | | |
| 1 | | | | |
| 2 | | | | |
| 3 | | | | |
Таблица 2.
| | 5 | 20 | 28 | 35 | 40 |
| 1 | | | | | |
| 2 | | | | | |
| 3 | | | | | |
h =
Таблица 3.
| | 2 | 4 | 6 | 8 | |
| 1 | | | | | |
| 2 | | | | | |
| 3 | | | | | |
h =
При N = N0/2 в Таблицу 2 занесите высоты столбиков hk в пяти ячейках (центральной и удаленных от нее на разные расстояния), а также суммарную высоту h столбиков во всех ячейках (не в пяти выбранных, а именно во всех ячейках).
При N = N0 в Таблицу 3 занесите высоты столбиков hk во всех четных (или нечетных) ячейках, а также суммарную высоту h столбиков во всех ячейках подряд.
Обработка результатов.
-
Флюктуации относительной частоты.
Сравните флюктуации относительной частоты в одной из средних ячеек при разных N. Сравните флюктуации относительной частоты при одном N в одной из средних ячеек и в одной из крайних ячеек. Сравните средние значения относительной частоты при разных N для одинаковых ячеек. Согласуются ли опыты с законом больших чисел?
-
Закон распределения частиц по ячейкам доски Гальтона.
Постройте график зависимости вероятности Pk от номера ячейки k. За приближенное значение вероятности примите среднее значение относительной частоты
, полученное в опытах с полным стаканом. Значение 
найдите по экспериментальным данным, зафиксированным в Таблице 3. При построении графика берите больше значений k в области, где hk быстро меняется при переходе к соседним ячейкам.Для построения функции Pkт примите за
то значение k, при котором получился максимум экспериментальной кривой. Значение стандарта , которое необходимо для построения теоретической кривой Pkт можно вычислить двумя способами: 1) полагая совпадающими максимальные значения функций Pk и Pkт
; 2) принимая, что стандарт равен полуширине экспериментальной кривой на уровне 
. Оба способа дадут одинаковые значения , если выполняется закон Гаусса.Задание 3.
Интегральный и дифференциальный законы распределения для непрерывной случайной величины. Приводятся 2 варианта задания, которые выполняются для разных случайных величин с разной аппаратурой.
А) При изготовлении резисторов с заданным значением сопротивления из-за многих мелких отклонений от нормального технологического процесса получается разброс значений сопротивления R, который можно описать с помощью закона распределения.
Чтобы получить экспериментально этот закон, измерьте при помощи мостика Уитстона сопротивления 100 образцов резисторов с одинаковой маркировкой. Полученные при измерении значения случайной величины R отметьте на числовой оси. Если значения повторяются, отметьте их штрихами над осью. Используя эти измерения, постройте интегральную функцию распределения F(r) для случайного результата измерения R, пользуясь приближенным равенством
, где N – общее число измерений. N’ – число значений R, которые меньше r.Постройте график дифференциальной функции распределения путем графического дифференцирования функции F(r). На том же рисунке постройте график плотности вероятности для нормального распределения
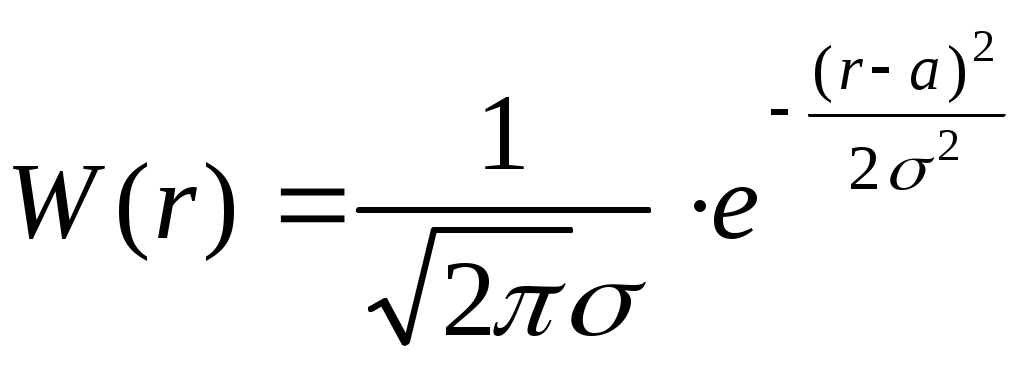. За a примите наиболее вероятное значение величины R, полученное при эксперименте, а за – полуширину экспериментальной кривой на уровне 
(
). Сравните стандарт с погрешностью, которую дает мостик, использованный для измерений.Сравните a со значением сопротивления R0, указанным на резисторах. Сравните систематическую и случайную погрешности изготовления резисторов (a – R0)/a и /a с погрешностью, указанной на образцах.
Б) Измерьте при помощи мостика УМ-2 емкость 100 образцов конденсаторов с одинаковой маркировкой. Разброс полученных значений емкости C тоже связан со случайными отклонениями от нормального технологического процесса. Результаты обработайте так же, как указано в задании А).