ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 25
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» |
| Кафедра экономики и управления Форма обучения: очно-заочная |
ВЫПОЛНЕНИЕ
ПРАКТИЧЕСКИХ ЗАДАНИЙ
ПО ДИСЦИПЛИНЕ
МАТЕМАТИКА
Группа 22ГУ171в
Студент
А.С. Капытко
МОСКВА 2023
Содержание:
1. Методом изоклин построить интегральные кривые уравнения
1.1.
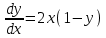 .
.2. Решить уравнение, допускающее понижения порядка
2.1.
3. Решить систему уравнений
3.1.

4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10?
Практические задания
1. Методом изоклин построить интегральные кривые уравнения:
1.1.
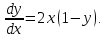
Решение:
Уравнение изоклин:
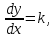
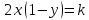 , где
, где 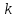 - const, откуда
- const, откуда 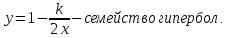
1) при
 имеем
имеем 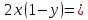 0,
0, 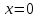 или
или 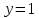 , таким образом,
, таким образом, 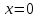
- линия экстремумов,
 - не линия экстремумов, так как является частным решением уравнения, и на основании теоремы существования и единственности решения через её точки не могут проходить других интегральные кривые.
- не линия экстремумов, так как является частным решением уравнения, и на основании теоремы существования и единственности решения через её точки не могут проходить других интегральные кривые.2) при
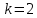 уравнения изоклин имеет вид:
уравнения изоклин имеет вид:  2, далее:
2, далее: 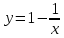 , в точках пересечения с данной изоклиной, касательные интегральных кривых образуют с осью
, в точках пересечения с данной изоклиной, касательные интегральных кривых образуют с осью  угол
угол 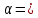
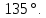
3) при
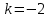 уравнения изоклин имеет вид
уравнения изоклин имеет вид 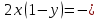 2, далее:
2, далее: 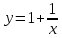 , угол наклона отрезков касательных составляет
, угол наклона отрезков касательных составляет 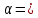
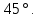
На изоклине, где
 , могут находиться точки максимума и минимума интегральных кривых. Для большей точности построения кривых найдём вторую производную
, могут находиться точки максимума и минимума интегральных кривых. Для большей точности построения кривых найдём вторую производную 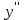 , чтобы найти геометрическое место точек и определить выпуклость или вогнутость кривых.
, чтобы найти геометрическое место точек и определить выпуклость или вогнутость кривых. Так как
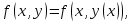 то
то 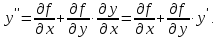
В нашем случае:
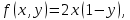
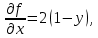
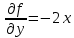 , тогда
, тогда , подставляя вместо
, подставляя вместо 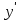 значение функции
значение функции 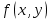 , получим:
, получим: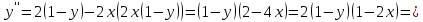
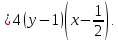
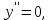
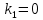
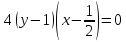
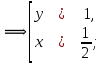 - частное решение.
- частное решение.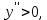
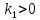
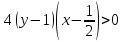
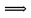
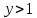 – кривая вогнута,
– кривая вогнута, 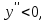
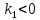
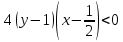
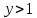 – кривая выпукла.
– кривая выпукла.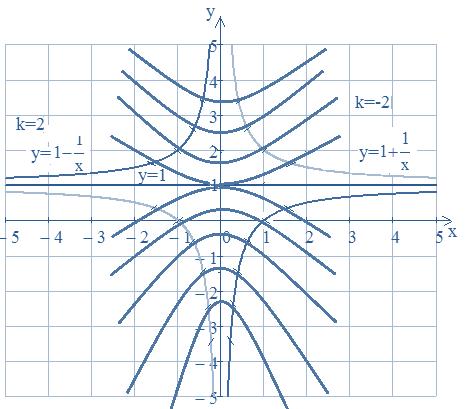
Рис.1. Построение интегральных кривых уравнения методом изоклин
2. Решить уравнение, допускающее понижение порядка:
2. 1.

Решение:
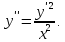
Данное уравнение вида
 допускающее понижение порядка, которое не содержит явно искомой функции
допускающее понижение порядка, которое не содержит явно искомой функции 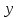 .
.Пусть
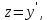 тогда
тогда 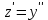 , получим уравнение:
, получим уравнение: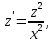
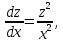
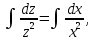
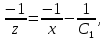
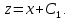
 следовательно,
следовательно, 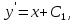 откуда получим:
откуда получим: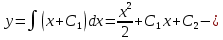
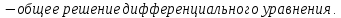
Ответ:
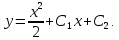
3. Решить систему уравнений:
3. 1.
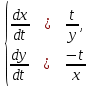
Решение:
Воспользуемся методом интегрируемых комбинаций.
Разделим первое уравнение на второе, получим:
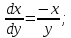
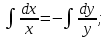
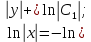
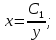
Разделим второе уравнение на первое:
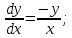
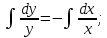
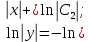
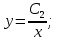
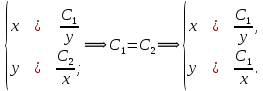
Ответ:
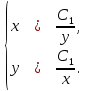
4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появления события равнялось 10?
Решение:
Наивероятнейшее число наступлений события А в схеме Бернулли находится по формуле:
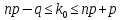
В данном случае
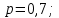
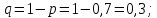
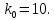
Согласно неравенству:
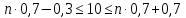
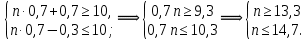
следовательно, необходимо провести 14 испытаний.
Ответ: 14 испытаний.