ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 16
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
4 МАТЕМАТИКАЛЫҚ БАҒДАРЛАМАЛАУ
Математикалық бағдарламалау- қолданбалы математиканың белгілі бір шектерді сақтай отырып фунцияның максимал мен минимал мәнін іздеуге бағытталған бір бөлімі.
Есептеу келісідей реттілікпен жүзеге асады:
Мысалы: белгілі бір функцияның максималданатын (минималданатын)
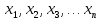 айнымалыларын анықтау қажет. Бұл жағдайда өрнек келесі түрде жазылады:
айнымалыларын анықтау қажет. Бұл жағдайда өрнек келесі түрде жазылады:L=f(
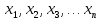 ) (1)
) (1)Келесідей теңсіздіктердің орындалуы кезінде:


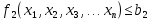
---------------------------------- (2)

Есептің шегіне қойылатын ең негізгі шарт бірқатар немесе барлық айнымалылардың оң мәнді болуы

(1)-ші функция,яғни максимум және минимум табу қажет етілетін функция есептің - мақсатты функциясы деп аталады.
Шектеу жүйесі (2) оң мәнді болу шартымен бірігіп
 кеңістігінде айнымалылардың рұқсат етілетін мәндерінің аймағын құрайды. Рұқсат етілетін мәндер аймағының ішінен таңдалған
кеңістігінде айнымалылардың рұқсат етілетін мәндерінің аймағын құрайды. Рұқсат етілетін мәндер аймағының ішінен таңдалған 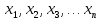 айнымалылар мәнінің жиынтығы- тапсырманың жоспары деп аталады.
айнымалылар мәнінің жиынтығы- тапсырманың жоспары деп аталады.Ал L функциясының максимумы (минимумы) мәніне сәйкес келетін жоспар – тиімді жоспар деп аталады.
Мақсатты функцияның және шектеу жүйесінің түріне байланысты математикалық бағдарламалар тапсырмалары екіге бөлінеді:
-
Сызықты бағдарламалау тапсырмалары – егер мақсатты функция және оның барлық шектеулері айнымалыларына қатысты сызықты болса
айнымалыларына қатысты сызықты болса -
Сызықсыз бағдарламалау тапсырмалары- егер керісінше сызықсыз байланыста болса.
4.1 Сызықты бағдарламалау тапсырмаларын орындау тәртібі
Қарастырылатын көптеген жоспарлау, жобалау, құрылыс және эксплуатация тапсырмалары – сызықты бағдарламалау қатарына жатады. Мақсатты функция ретінде шығыстар мен шығындар, кірістер, өнімнің өндірілуі қарастырылады. Ал айнымалылар ретінде – барлық қажетті ресурстар, қорлар, жабдықтар және т.б қарастырылады.
Мысалы: D1 және D2 станоктарында өнімнің екі түрі A1 және А2 өндіріледі.
A1 өнімді өндіру үшін D1 станогы 2 сағат жұмыс жасайды;
D2 станогы 1 сағат жұмыс жасайды;
A2 өнімді өндіру үшін D1 станогы 1 сағат жұмыс жасайды;
D2 станогы 2 сағат жұмыс жасайды;
Бір тәулік ішінде D1-10 сағаттан артық жұмыс жасамайды;
D1-8 сағаттан артық жұмыс жасамайды.
Станоктардың жұмыс жасамай тұрып қалуы шығынға әкеледі. 1 сағат тоқтап тұруы:D1 – 200тн, D2 – 100тн.
Таза пайда максимал болатындай бір тәулік ішінде өндірілетін өнім жоспарын құру қажет.
Таза пайда – бұл өндірілген өнімнен түскен пайдадан станоктардың тоқтап тұруынан болатын шығынның айырмасы.
Тиімді мәні →max.
10
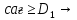
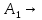 2 сағ
2 сағ 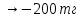
8сағ

 1 сағ
1 сағ

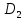
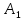
 1 сағ
1 сағ
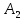
 2 сағ
2 сағ Айнымалылардың белгіленуі:
 -
- өнімінің 1 тәуліктегі мөлшері
өнімінің 1 тәуліктегі мөлшері -
-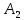 өнімінің 1 тәуліктегі мөлшері
өнімінің 1 тәуліктегі мөлшері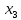 -
- станогының тоқтап тұру уақыты
станогының тоқтап тұру уақыты -
-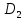 станогының тоқтап тұру уақыты
станогының тоқтап тұру уақыты f- таза пайдa
Есептің шарты:
f=500
 +200
+200 -200
-200 -100
-100 =max (1)
=max (1)Төрт аргументтен тұратын функция. Төрт шаманың жиынтығы – жоспар.
Мақсатты функцияның максимумы ізделінетін жоспар аймағы анықталады.
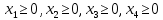 (2)
(2)Тәуліктегі станоктардың жұмыс жасау уақыты:
D1 2x1+ x2 ;
D2 x1 + 2x2.
Егер станоктардың тоқтап тұруын ескерсек:

 (3)
(3)
Бұл тапсырмада айнымалылар саны шектеу шартын көп 4>2. Сол себепті x3 және x4 айнымалыларын x1 және x2 арқылы өрнектеуге болады:
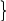
 (4)
(4)
(4) өрнекті (1) және (3) теңсіздіктерге қою арқылы келесідей нәтижеге қол жеткіземіз:
f= -2800+1000
 +600
+600 (5)
(5) Шарт келесідей сипатқа ие болады:
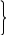 2
2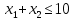
 +2
+2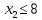 (6)
(6)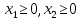
Тапсырма →берілген (6) теңсіздік шешімінің аймағында (5) функциясының ең үлкен мәнін анықтау.
Бұл мысалды талдау арқылы математикалық бағдарламалау тапсырмаларын құру жолдары меңгеріледі.