Файл: Смеси идеальных газов. Термодинамические процессы с идеальным газом.docx
Добавлен: 10.01.2024
Просмотров: 39
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– изменение дельной энтальпии
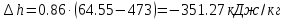 ;
;
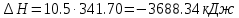 .
.
Изменение удельной энтропии в политропном процессе определяют по формуле:
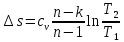 ;
;
Изменение энтропии определяется по формуле:
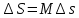 .
.
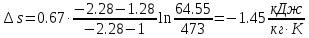 ;
;
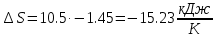 .
.
Адиабатный процесс – процесс без изменения энтропии. Уравнение адиабаты называют уравнением Пуассона:
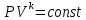 ;
;
Показатель адиабаты k был вычислен ранее. k=1.28
Давление P2 можно найти через связь между параметрами состояния в адиабатном процессе:
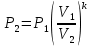 ;
;
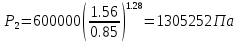 .
.
Температуру Т2 определяем по отношению:
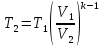 ;
;
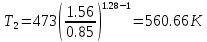 .
.
По первому закону термодинамики, при отсутствии теплообмена с окружающей средой работа адиабатного процесса осуществляется за счет внутренней энергии:
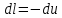 .
.
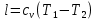 ;
;
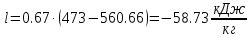 ;
;
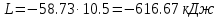 .
.
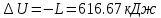 .
.
В адиабатном процессе ds=0, следовательно dq=ds∙T=0.
ΔS=0, ΔQ=0
 ; где
; где  – изменение дельной энтальпии
– изменение дельной энтальпии
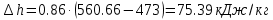 ;
;
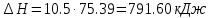 .
.
Изотермный процесс – процесс, проходящий при постоянной температуре. Уравнение изотермы:
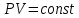 .
.
Давление P2 можно найти через связь между параметрами состояния в изотермном процессе:
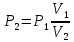 ;
;
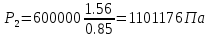 ;
;
Т2=T1=473 К
В случае постоянства температуры в процессе внутренняя энергия и энтальпия остаются постоянными
ΔU=0; ΔH=0
 ; где
; где 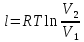 – удельная работа изотермного процесса.
– удельная работа изотермного процесса.
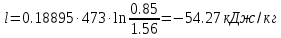 ;
;
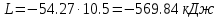 .
.
По первому закону термодинамики dU=dQ-dL. Т.к. dU=0, dQ=dL
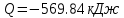 .
.
Изменение энтропии изотремного процесса:
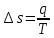 ;
;
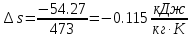 ;
;
 ;
;
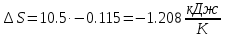 .
.
Сводная таблица результатов расчета:
Вывод
Зная молярные (или массовые) доли компонентов смеси, можно вычислить основные параметры состава смеси: среднюю (кажущуюся) молярную теплоемкость, газовую постоянную, плотность, удельный объем, парциальное давление компонентов.
Зная одну из удельных теплоемкостей (массовую, молярную, объемную, изобарную или изохорную), можно рассчитать другие. Если зависимость теплоемкости от температуры нелинейная, то средняя теплоемкость определяется в интервале температур.
Рассчитав показатель политропы, можно определить, к какому термодинамическому процессу относится данный процесс. Также его можно определить графически, по P-V и T-S диаграммам.
Список литературы
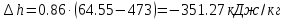 ;
;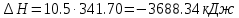 .
.Изменение удельной энтропии в политропном процессе определяют по формуле:
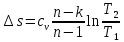 ;
;Изменение энтропии определяется по формуле:
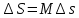 .
.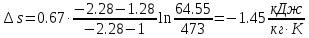 ;
;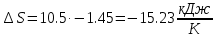 .
.Адиабатный процесс – процесс без изменения энтропии. Уравнение адиабаты называют уравнением Пуассона:
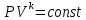 ;
;Показатель адиабаты k был вычислен ранее. k=1.28
Давление P2 можно найти через связь между параметрами состояния в адиабатном процессе:
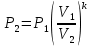 ;
;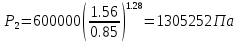 .
.Температуру Т2 определяем по отношению:
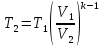 ;
;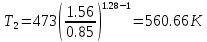 .
.По первому закону термодинамики, при отсутствии теплообмена с окружающей средой работа адиабатного процесса осуществляется за счет внутренней энергии:
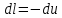 .
.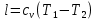 ;
;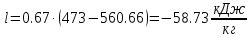 ;
;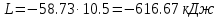 .
.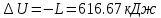 .
.В адиабатном процессе ds=0, следовательно dq=ds∙T=0.
ΔS=0, ΔQ=0
 ; где
; где  – изменение дельной энтальпии
– изменение дельной энтальпии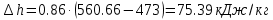 ;
;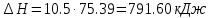 .
.Изотермный процесс – процесс, проходящий при постоянной температуре. Уравнение изотермы:
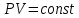 .
.Давление P2 можно найти через связь между параметрами состояния в изотермном процессе:
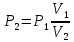 ;
;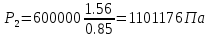 ;
;Т2=T1=473 К
В случае постоянства температуры в процессе внутренняя энергия и энтальпия остаются постоянными
ΔU=0; ΔH=0
 ; где
; где 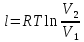 – удельная работа изотермного процесса.
– удельная работа изотермного процесса.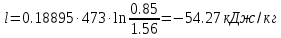 ;
;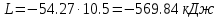 .
.По первому закону термодинамики dU=dQ-dL. Т.к. dU=0, dQ=dL
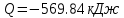 .
.Изменение энтропии изотремного процесса:
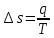 ;
;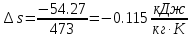 ;
; ;
;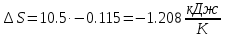 .
.Сводная таблица результатов расчета:
| Вычисленные величины | Политропный процесс | Адиабатный процесс | Изотермный процесс |
| V1, м3 | 1.56 | 1.56 | 1.56 |
| V2, м3 | 0.85 | 0.85 | 0.85 |
| P1, Па | 600000 | 600000 | 600000 |
| P2, Па | 150000 | 1305252 | 1101176 |
| T1, К | 473 | 473 | 473 |
| T2, К | 64.55 | 560.66 | 473 |
| Характер процесса | сжатие | сжатие | сжатие |
| n | -2.28 | 1.28 | 1 |
| L, кДж | -245.28 | -616.67 | -569.84 |
| Q, кДж | -3118.71 | 0 | -569.84 |
| ∆U, кДж | -2873.43 | 616.67 | 0 |
| ∆H, кДж | -3688.34 | 791.60 | 0 |
| ∆S, кДж/К | -15.23 | 0 | -1.208 |
Вывод
Зная молярные (или массовые) доли компонентов смеси, можно вычислить основные параметры состава смеси: среднюю (кажущуюся) молярную теплоемкость, газовую постоянную, плотность, удельный объем, парциальное давление компонентов.
Зная одну из удельных теплоемкостей (массовую, молярную, объемную, изобарную или изохорную), можно рассчитать другие. Если зависимость теплоемкости от температуры нелинейная, то средняя теплоемкость определяется в интервале температур.
Рассчитав показатель политропы, можно определить, к какому термодинамическому процессу относится данный процесс. Также его можно определить графически, по P-V и T-S диаграммам.
Список литературы
-
Теплотехника: Учеб. для вузов / В.Н.Луканин, М.Г.Шатров, Г.М.Камфер и др.; Под ред. В.Н.Луканина. – 3-е изд., испр. – М.Ж Высш. шк., 2002. - 671 с. -
Техническая термодинамика: Рук-во к лаб.работам / Сост. И.Х.Хайруллин., Казань, КХТИ, 1995, 48с.