Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования

Санкт-Петербургский горный университет

Кафедра Общей и технической физики
По дисциплине: Физика
Расчетно-графическое задание

Вариант 23

Раздел: Механика
Тема «Движение материальной точки (вращательное движение)»

Выполнил: студент гр. /./

^{(шифр группы) (подпись) (Ф.И.О.)}

Проверил: ________ /_______________/

(подпись) (Ф.И.О.)


Дата:____________________

Оценка:

Санкт-Петербург

2012
Задача.

Конус массой 520 кг. вращается без начальной скорости вокруг своей оси. На тело действует пара сил с моментом 20,5 Дж и моментом сопротивления Mсопр=kω². Сколько оборотов сделает цилиндр до того, как его угловая скорость станет равной 3,45 рад/с? (k=2,5 кг·м² ,R=0,6 м) Построить графики зависимостей момента силы и угловой скорости от времени

Краткое теоретическое содержание:

Явление,изучаемое в задаче:

В данной задаче рассматривается явление вращательного движения и понятия момента силы, пары сил, момента инерции, угловой скорости, углового ускорения.

Определение основных физических понятий, объектов, Процессов и величин.

Вращательное движение твёрдого тела – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.

Момент силы относительно неподвижной точки – это физическая величина, определяемая векторным произведением радиуса-вектора

---

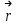, проведённого из точки О в точку А приложения силы, на силу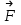

Модуль момента силы



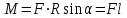
де α – угол между 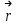и 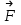; r·sinα=l – плечо силы.

Плечо силы – длина, перпендикулярно-опущенная из заданной точки на прямую, вдоль которой действует сила.

Момент силы относительно неподвижной оси – проекция момента силы относительно точки на ось произвольно проходящей через данную точку.

М 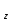- скалярная величина, не зависящая от выбора положения точки на ось.

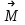- момента силы.

Пара сил – это две равные по модулю, но противоположные по направлению и не действующие вдоль одной прямой силы. Плечо пары сил-расстояние между прямыми, вдоль которых действуют силы.

Угловая скорость – это векторная величина ω, модуль которой определяется пределом отношения поворота тела на угол Δφ за время Δt к этому времени, при стремлении последнего к нулю:



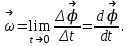
где 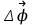- изменение угла поворота за время .

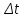Модуль угловой скорости –величина, которая определяет угол поворота в единицу времени и характеризует быстроту вращения:



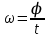
Единица угловой скорости [ 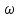]=1 рад/с.

Угловое ускорение – это векторная величина, определяемая первой производной угловой скорости по времени:

.

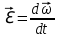При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости.

---

Модуль углового ускорения – величина, характеризующая изменение модуля угловой скорости в течении времени.

Единицы измерения угловой скорости [ω] =рад/с

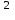
Момент инерции тела относительно оси вращения -это физическая величина, равная сумме произведений элементарных масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
.

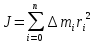В случае непрерывного распределения масс эта сумма сводится к интегралу:
J= ,

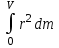Величина r в данном случае есть функция положения точки с координатами x,y,z.
Решение задачи

Дано:

R = 0,6м

m =520кг

М=20,5 Дж М_сопр.=kω²

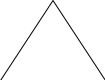
k=2,5 кг•м

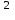
ω=3,45 рад/с

Найти: N -?








Согласно основному уравнению динамики вращательного движения твердого тела относительно неподвижной оси:

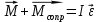
Спроецируем векторы на ось Oz: 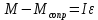(1)

Введём формулу момента инерции конуса относительно оси вращения (центра):

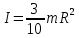(2)

Из условия задачи знаем: 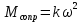(3)

Вспомним, что угловое ускорение – это производная угловой скорости по времени. Преобразуем угловое ускорение, для этого домножим числитель и знаменатель на dφ, чтобы получить угловую скорость, которая равна

---

:

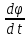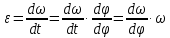(4)

Теперь подставим выражения в уравнение (1) выражения (2), (3), (4):



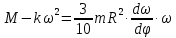
Перенесем 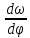в левую сторону: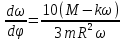

Перевернём дробь:

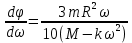
Представим 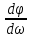в виде производной: 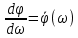= 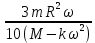(5)

Возьмём интеграл от φ: ;

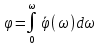Подставим теперь выражение (5) в интеграл: ;









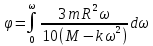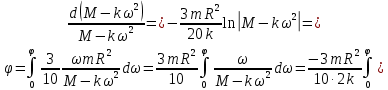
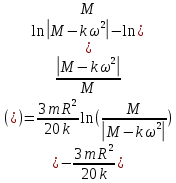
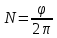
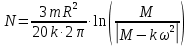
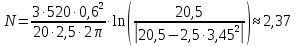
Проверим размерность: 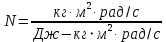= 1→ N-безразмерная величина

Графики

График зависимости момента силы от времени:

Момент силы остается равным 20,5 Дж на протяжении всего времени наблюдения.

Графиком будет прямая, параллельная оси времени.



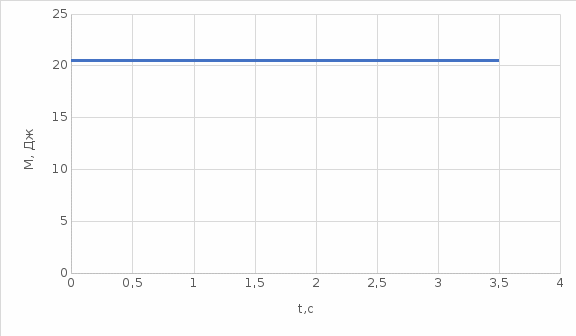
График зависимости угловой скорости от времени.

В основное уравнение динамики вращательного движения: 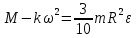подставим ω=1рад/c и найдем угловое ускорение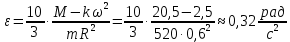



Уравнение равноускоренного движения:



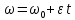
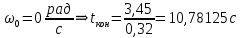
График будет представлять из себя прямую, исходящую из начала координат.

---

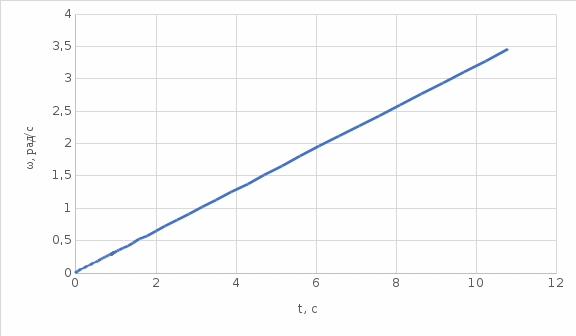
Вывод:

В данной расчётно-графической работе мы вычислили количество оборотов равное 2,37, сделанное конусом, до того, как его угловая скорость стала равной 3,45 рад/с.

---

Смотрите также файлы

• Учебная программа по предмету История Казахстана для 59 классов уровня основного среднего образования (с русским языком обучения).pdf

• Практическая работа 3 Задание 1.docx

• Задание Вспомнив, материалы лекций, вам необходимо понять оценка это или факт.docx

• 1. Метрологическое обеспечение и его структура. Магнитоэлектрический измерительный механизм.doc

• Итоговый индивидуальный проект метеориты и астроблемы.docx