Файл: Решение Фигура 1 прямоугольник b32мм h185мм Фигура 2 швеллер 16а по сортаменту.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 12
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1)
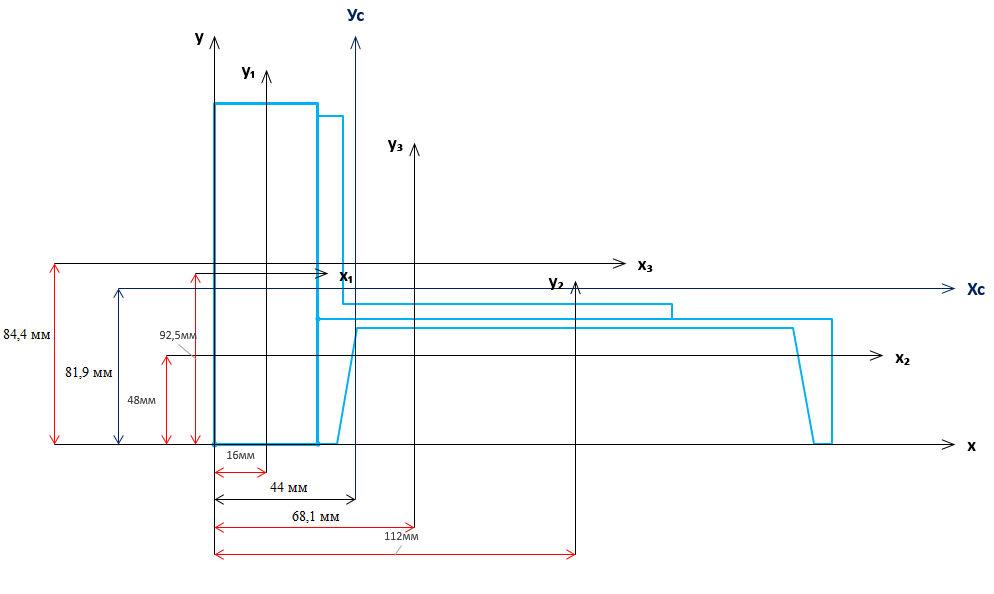
| Решение: |
| Фигура №1: прямоугольник: b₁=32мм; h₁=185мм; |
| Фигура №2: швеллер 16а: по сортаменту; |
| Фигура №3: уголок 11*110*8: b₃=110мм; |
| Проводим дополнительные оси центров тяжести фигур относительно главных осей. |
| Их координаты: |
| x₁=16мм; x₂=112мм; x₃=68,1мм; |
| y₁=92,5мм; y₂=48мм; y₃=84,4мм; |
| Площади сечений фигур: |
| А₁=b₁·h₁=32мм·185мм=5920мм² |
| А₂=1950мм² |
| А₃=1390мм² |
| Сумма площадей: |
| А=А₁+А₂+А₃=5920мм²+1950мм²+1390мм²=9260мм² |
| Статические моменты инерции относительно оси Х: |
| Sx₁=А₁·y₁=5920мм²·92,5мм=547600мм³ |
| Sx₂=А₂·y₂=1950мм²·48мм=93600мм³ |
| Sx₃=А₃·y₃=1390мм²·84,4мм=117316мм³ |
| Sx=Sx₁+Sx₂+Sx₃=547600мм³+93600мм³+117316мм³=758516мм³ |
| Статические моменты инерции относительно оси У: |
| Sу₁=А₁·x₁=5920мм²·16мм=94720мм³ |
| Sу₂=А₂·x₂=1950мм²·112мм=218400мм³ |
| Sу₃=А₃·x₃=1390мм²·68,1мм=94659мм³ |
| Sу=Sу₁+Sу₂+Sу₃=94720мм³+218400мм³+94659мм³=407779мм³ |
| Моменты инерции фигур относительно своих осей: |
| Осей Х: |
| Ix₁=(b₁·h₁³)/12=(32мм·(185мм)³)/12=16884333,33мм⁴ Iy₁=(b₁³·h₁)/12=((32мм)³·185мм)/12=505173.33мм⁴ |
| Ix₂=788000мм⁴ Iy₂=8230000мм⁴ |
| Ix₃=1720000мм⁴ Iy₃=546000мм⁴ |
| Находим центр тяжести фигуры: |
| Xc=Sу/А=407779мм³/9260мм²=44мм |
| Yc=Sx/А=758516мм³/9260мм²=81,9мм |
| Указываем положение центра тяжести всей фигуры. |
| Проводим через него центральные оси Хс и Yс. |
| Моменты инерции фигур относительно центра тяжести: |
| Ixс₁=Ix₁+(y₁-Yc)²·А₁=16884333,33мм⁴+(92,5мм-81,9мм)²·5920мм²=17549504.53мм⁴ |
| Iyс₁=Iy₁+(x₁-Xc)²·А₁=505173,33мм⁴+(16мм-44мм)²·5920мм²=5146453.33мм⁴ |
| Ixс₂=Ix₂+(y₂-Yc)²·А₂=788000мм⁴+(48мм-81,9мм)²·1950мм²=3028959.5мм⁴ |
| Iyс₂=Iy₂+(x₂-Xc)²·А₂=8230000мм⁴+(112мм-44мм)²·1950мм²=17246800мм⁴ |
| Ixс₃=Ix₃+(y₃-Yc)²·А₃=1981700мм⁴+(84,4мм-81,9мм)²·1390мм²=1990387.5мм⁴ |
| Iyс₃=Iy₃+(x₃-Xc)²·А₃=1981700мм⁴+(68,1мм-44мм)²·1390мм²=2789025.9мм⁴ |
| Находим центральные осевые моменты инерции фигуры: |
| Ixс=Ixс₁+Ixс₂+Ixс₃=17549504.53мм⁴+3028959.5мм⁴+1990387.5мм⁴=22568851.33мм⁴ |
| Iyс=Iyс₁+Iyс₂+Iyс₃=5146453.33мм⁴+17246800мм⁴+2789025.9мм⁴=25182279.23мм⁴ |
3)
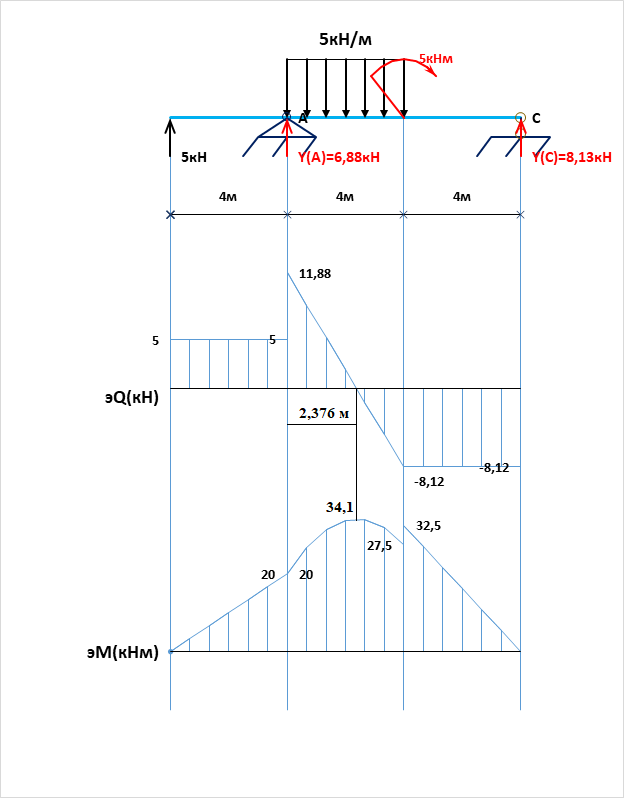
| Находим реакции в опорах: |
| ∑Fkx=X(A)=0 |
| ∑m(A)Fk=Y(C)∙8м-5кНм-5кН∙4м-5кН/м∙4м∙2м=0; |
| Y(C)=(+5кНм+20кНм+40кНм)/8м=8,13кН; |
| ∑m(C)Fk=-Y(A)∙8м-5кНм-5кН∙12м+5кН/м∙4м∙6м=0; |
| Y(A)=(-5кНм-60кНм+120кНм)/8м=6,88кН; |
| Проверка: |
| ∑Fky=Y(A)+Y(C)+5кН-5кН/м∙4м=0; |
| 6,88кН+8,13кН+5кН-5кН/м∙4м=0; |
| 0=0; проверка сходится. |
| Строим эпюры поперечных сил и изгибающих моментов. |
| В сечениях где эQ пересекает нулевую линию, поэтому на эМ будет экстремум. |
| Найдем длины на этих участках. |
| 2 участок: |
| 11,88кН/z₂=8,12кН/(4м-z₂); 11,88кН∙(4м-z₂)=8,12кН∙z₂; |
| 47,52кНм-11,88кН∙z₂=8,12кН∙z₂; 8,12кН∙z₂+11,88кН∙z₂=47,52кНм; |
| z₂=47,52кНм/(20кН)=2,376м |
| Запишем условие прочности: |
| maxσ≤[σ] |
| [σ]=160МПа |
| Находим максимальное напряжение: |
| maxσ=(34,1∙кНм)/Wx |
| σᵢ/[n]≥(34,1∙кНм)/Wx |
| Рассмотрим сечение: |
| Форма сечения: окружность |
| Wx=(π∙(d)³)/32=0,098d³ |
| Выражаем и определяем момент сопротивления: |
| Wx=(34,1∙кНм)/σт=(34,1∙1000Нм)/(160∙10⁶Па)=0,2131·10-3м³=2131000мм³; |
| Находим размеры сечения: |
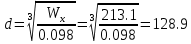
| Полученное значение округляем по ГОСТ 6636-69 (Ra20): |
| d=140мм. |