ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 19
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
КАЗАНСКИЙ ИННОВАЦИОННЫЙ УНИВЕРСИТЕТ ИМ. В.Г. ТИМИРЯСОВА (ИЭУП)
ЛАБОРАТОРНАЯ РАБОТА № 1 ПО ЭКОНОМЕТРИКЕ
Тема: Парная линейная регрессия
Вариант 9
Выполнила:
студент группы № 1001з
факультета “Прикладная информатика”
Петрова Елена Геннадьевна
зачетная книжка № 20-10-09з
Руководитель:
ст. преп. Аглямова З. Ш.
Казань – 2023г.
Решение:
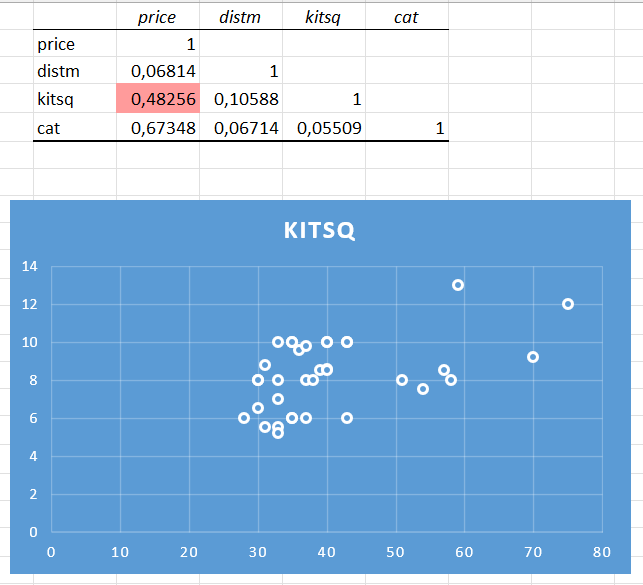
По рисунку видно, что наибольшее значение линейного коэффициента корреляции с зависимой переменной y принадлежит фактору жилая площадь – ryx = 0,483. Поэтому именно этот доминирующий фактор будем использовать для построения уравнения парной линейной регрессии.
Вывод 1: Как видно из рисунка 2, наблюдается прямая умеренная взаи- мосвязь между ценой квартиры (y) и площадью кухни квартиры (x). Точки на графике сосредоточены вокруг прямой линии, поэтому взаимосвязь между ценой и площадью квартиры уместно аппроксимировать прямой линией и применить линейную регрессию с одной объясняющей переменной.
 Вывод 2: Запишем модель линейной регрессии: y16,278 2,94x .
Вывод 2: Запишем модель линейной регрессии: y16,278 2,94x .Экономическая интерпретация коэффициентов следующая. Увеличение площади кухни на 1 кв.м приводит при прочих равных условиях к увеличению стоимости жилья на 2.94 тыс. USD. Данный результат согласуется с экономической интуицией, так как при росте площади кухни можно ожидать увеличения её стоимости.
Вывод 3: Согласно шкале Чеддока-Снедекора наблюдается умеренная прямая статистическая взаимосвязь между ценой и жилой площади квартиры
.
Вывод 4: Увеличение площади кухни на 1% приводит к увеличению цены на 0,6%
9-11.
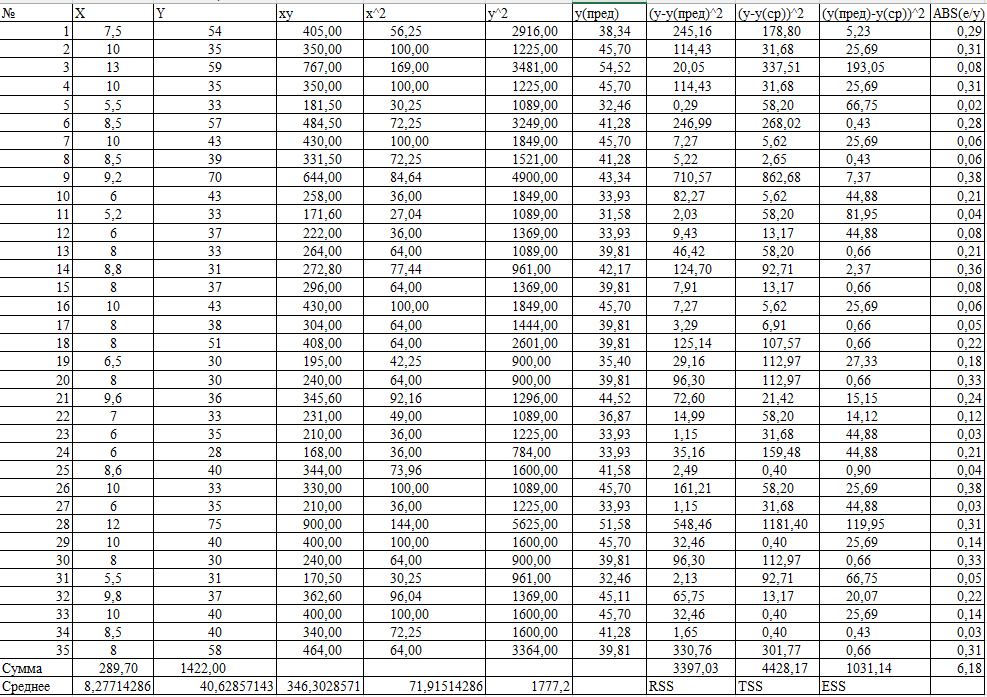
12-20.

Рисунок 8. Задачи 12-14
Вывод 5: Доля дисперсии цены, объясненная с помощью жилой площади квартиры, составляет 23,29%. Чем ближе R^2 к 1, тем лучше качество подгонки регрессии.
Вывод 6: Поскольку 3,1649 > 2,7332, то гипотеза Н0: β = 0 отвергается, т.е. согласно тесту Стьюдента коэффициент регрессии β является значимым. Это означает, что между переменными x (площадь кухни) и y (цена) существует значимая линейная связь.
Вывод 7: Диапазон границ доверительного интервала для коэффициента регрессии в модели с хорошим качеством подгонки обычно не превышает 3. В нашем случае, правая граница больше, чем левая, более чем в 3 раза, значит, качество подгонки модели рекомендуется улучшать.
Вывод 8: Поскольку 10,01 > 4,13, то гипотеза Н0: β = 0 отвергается, т.е. согласно тесту Фишера регрессия адекватна. Это означает, что между переменными x (площадь кухни) и y (цена) существует значимая линейная связь.
Вывод 9: Допустимый интервал средней ошибки аппроксимации – от 4% до 7%. Для построенной линейной парной регрессии средняя ошибка аппроксимации составила 17,64%, значит, качество подгонки модели рекомендуется улучшать, возможно, путем расширения модели до множественной регрессии через включение в нее дополнительных регрессоров.
21-24.