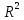Министерство науки и высшего образования РФ
Федеральное государственное бюджетное образовательное учреждение высшего образования

«Сибирский государственный индустриальный университет»


Кафедра естественнонаучных дисциплин им. профессора В.М. Финкеля

Контрольная работа Вариант 8

Выполнил:

Миллер А.В

ст.гр. ЗИС-221

22048


Новокузнецк 2023


Задача № 1

Дано:

X= + +

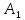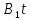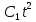
Y= + +

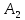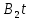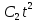
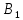=7 м/с

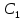=-2 м/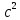

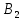=-1 м/с

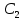=0,2 м/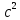

Найти:


V (t)-?


A (t)-?

Решение:

Запишем радиус-вектор. Он равен r=xi+yj, где i-орт оси X, а j-орт оси Y.

Поэтому получаем r=i× ( 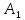+ +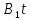 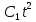)+j×( + + ).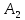

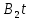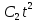Скорость есть производная перемещения по времени.

Поэтому V= 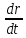= =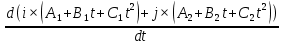i×(

---

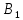
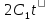+ )+j×( + )

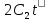Эта величина является вектором. Проекция скорости V на ось X равна

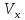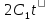= + , на ось Y равна 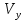= + 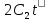. Тогда модуль скорости равен ║V║= +

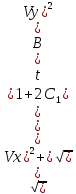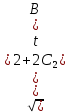
Подставляем числа:

║V║= 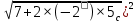+ 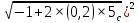=13 м/с

По определению ускорение это производная скорости по времени.

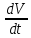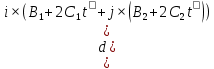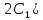Поэтому a= = =i×( +j× )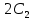

Проекция ускорения a на ось X равна ax=

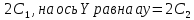
Поэтому ║a║= = +

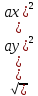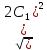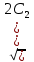
Подставляем числа.

║a║= 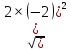+ 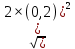=4,02 м/

Ответ: V(t)=13 м/с; A(t)=4,02 м/

Задача № 2

Дано:

M=200 кг

m=20кг

V=1м/с

Найти:

V1-?

V2-?

Решение:

Воспользуемся законом сохранения импульса. А так как задача симметрична

Относительно перестановки лодок (они абсолютно равны) и перебрасываемые грузы одинаковы, то скорость лодок будет равна по модулю

---

, но противоположны по направлению.

Поэтому рассматриваем одну лодку.

Для первой лодки.

M×V1= (M-m) ×V+m×V, где M-масса лодки, m-груза, V1-скорость лодки после перебрасывания грузов.

Проектируем вектора на ось X и получаем M×V1=(M-m) ×V-m×V

Откуда искомая скорость

V= 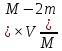= =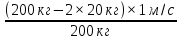0, 8 м/c

Ответ: V(1,2) =0,8 м/с


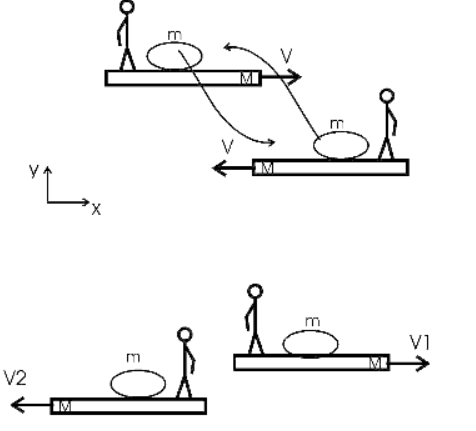
Задача № 3

Дано:

m=5кг

V0=1м/c

M=2кг

Найти:

V1=?

V2=?

Решение:

Шарики должны отскочить в разные стороны так как удар упругий, поэтому из закона сохранения импульса находим: m× 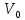=-m×V1+M×V2.

Из закона сохранения энергии получаем: = + .

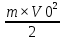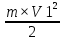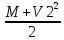Из первого уравнения находим скорость второго шара V2= .

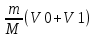Подставим во второе уравнение: 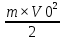= 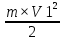+ 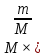(V0+V1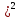

Упрощаем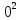: V =V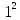 + 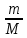×(V0+V1 .

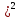Далее 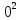V -V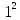 =(V0-V1)×(V0+V1)= 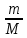×(V0+V1 .

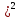Откуда получаем (V0-V1)= 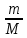×(V0+V1).

И в дальнейшем находим скорость первого шара после удара

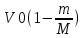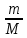V1= ÷(1+ )=V0(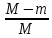

---

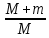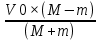)÷( )= , подставляем в

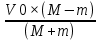V2= (V0+V1)= (V0+ ), подставим числа

V1= 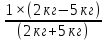=0,429 м/с.

Находим скорость второго шара: V2= 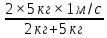=1,429 м/с

Ответ: V1=0,429; V2=1,429 (м/с)


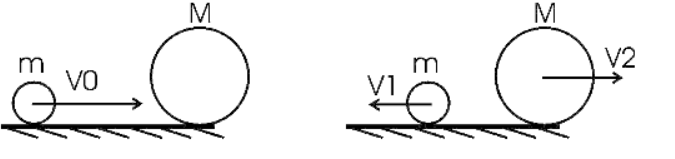
Задача № 4

Дано:

m=16 т

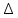x=8 см

V=0, 6 м/с

Найти:

k=?

Решение:

Кинетическая сила вагона до столкновения: Ek= 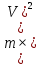, где V- скорость вагона.

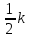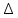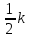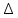Эта энергия идет на деформацию пружины. Энергия деформированной пружины: W= ( x , Тогда ( x = 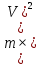, Откуда искомая величина равна

k= 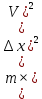, Подставляем числа: k= 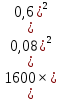=9,5×1 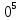H/m=0,9 MH/m

Ответ: k=0,9 MH/m.
Задача № 5

Дано:

m1=0,3 кг

m2=0,7 кг

m=0,4 кг

Найти:

Т1=?

Т2=?

Решение:

Веса первой и второй гири равны P1=m1×g и P2=m2×g соответственно.

Ввиду того, что масса нити пренебрежимо мала, изменения натяжений T1 и T2 вдоль нити можно не учитывать. Используем второй закон Ньютона и, одновременно проецируем силы на ось X. Тогда уравнение движение грузов и блока будут выглядеть следующим образом.

-m1×a=T1+m1×g (1)

m2×a=-T2+m2×g (2)

J 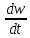=R×(T2-T1) (3)
Где J- момент инерции блока. Известно, что для однократного диска массой m и радиусом R момент инерции равен: J=

---

.

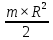Если проскальзывания нити по блоку, нет то =a, где а-ускорение грузов

-угловое ускорение блока. Тогда 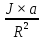=(T2-T1).

Из (1) и (2) уравнения находим (m1+m2)×a=-(T2-T1)+(m2-m1)×g, Подставляем (T2-T1) 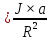и получаем (m1+m2)×a+ 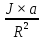=(m2-m1)×g ,откуда ускорение равно a= = = .

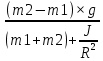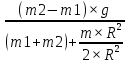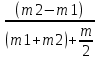Подставляем ускорение в (1) и находим Т1:

T1=m1×(g+a)=m1×( 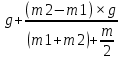)=m1×g×( ).

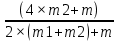Подставляем ускорение в (2) и находим Т2

T2=m2×(g-a)=m1×( 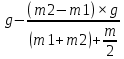)=m2×g×( ).

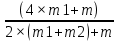Подставляем числа. T=0,3кг×9,81м/ ×( 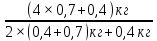)=3,92H.

T2=0,7кг×9,81м/ ×( 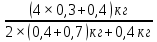)=4,58H.

Ответ: T1=3,92; Т2=4,58H.

Задача № 6

Дано:

D=0,8м

m1=6кг

m2=60кг

m=0,5кг

V=5м/с

R=0,4м

D=2×R

Найти:

w=?

Решение:

Мяч обладает моментом импульса относительно оси вращения: M=m×V×R. Воспользуемся законом сохранения импульса: (J1+J2+m× 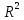)×w=M=m×V×R, где J1= = .

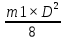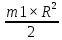Момент инерции скамьи D=2×R и массой m1, w-угловая скорость вращения человека с диском J1+J2-суммарный момент инерции диска и человека, находящегося на краю диска. Момент инерции человека J2=m2×

---

Смотрите также файлы

• .rtf

• Абсолютная монархия в Англии (конец xv середина xvii вв.).rtf

• Анализ по произведению русская народная песня.docx

• Абсолютная монархия во Франции (xvixviii вв.).rtf

• Измерение радиуса кривизны линзы методом интерференционных колец ньютона.docx