Таблица 4.1.3 Измерение углов дифракции для линий синего цвета

|m|	0	1	2	3
α+m	0	4,51	9,04	13,41
ᾱ+m	0	4,51	9,04	13,41
ϕ̅+m=ᾱ+m-ᾱ0	-	4,51	9,04	13,41
a=sinϕ̅+m/m	-	0,079	0,079	0,077
ϴa=cosϕ̅+m/m	-	0,997	0,494	0,324
ϴa=cosϕ̅-m/m	-	-0,997	-0,494	-0,324
a=sinϕ̅-m/m	-	0,079	0,078	0,077
ϕ̅-m=ᾱ-m-ᾱ0	0	-4,51	-9,03	-13,4
ᾱ-m	0	-4,51	-9,03	-13,4
α-m	0	-4,51	-9,03	-13,4

3. 
   По полученным выборкам значений объема по каждой из таблиц по форме 4.1 найти результат косвенного измерения выборочным методом обработки данных косвенных измерений с . Результаты занести в таблицу 4.3
   

Для примера приведен расчет углового параметра для зеленого цвета.

Находим СКО:

при и

Находим среднюю приборную погрешность

Из таблицы очевидно, что

---

Связано это с уже упомянутым выше фактором виртуального стенда. Значения при m=1 и m=-1 получились равными по модулю, но противоположными по знаку и в сумме каждо такая пара значений противоположных порядков дифракции даёт нуль.

Находим полную приборную погрешность :

В нашем случае:

Как итог, результат косвенного измерения:

Аналогично находим угловые коэффициенты для зеленого и синего цветов. Результаты заносим в табл. 4.3.

4. 
   В координатах отметить положение совместных значений для синей, зеленой и желтой линий, и через полученные совокупности точек провести аппроксимирующие прямые
   

График 4.1. Зависимость синуса угла дифракции от порядка дифракции, а также их аппроксимирующая функция для желтого цвета.



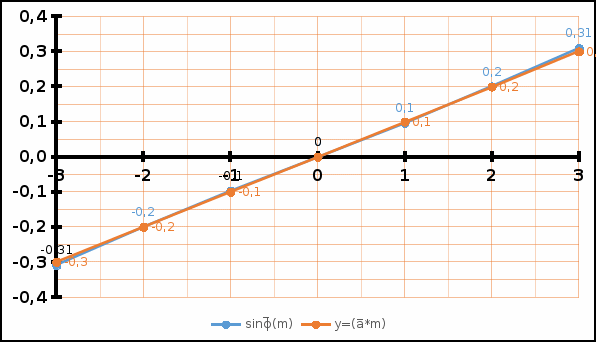
График 4.2. Зависимость синуса угла дифракции от порядка дифракции, а также их аппроксимирующая функция для зеленого цвета.



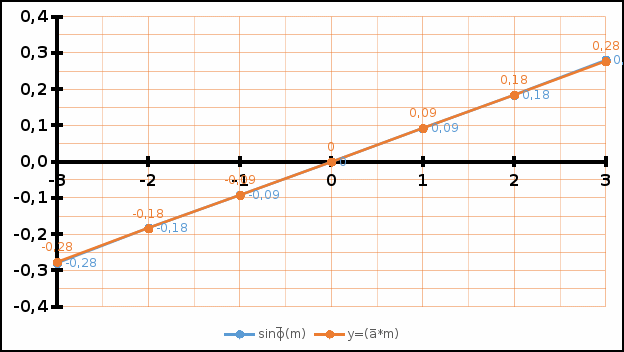
График 4.3. Зависимость синуса угла дифракции от порядка дифракции, а также их аппроксимирующая функция для синего цвета.



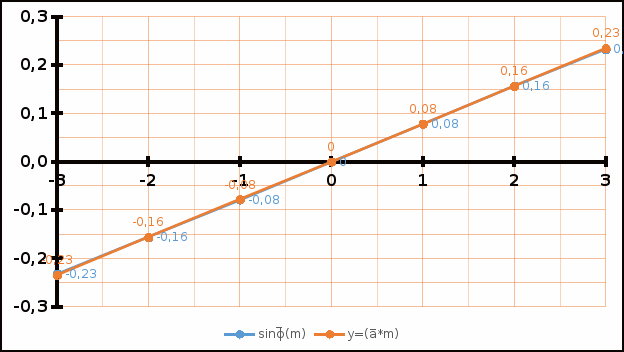
И снова из-за программной природы измерений, зависимость получилась строго линейной и их аппроксимации практически совпали. В случае реального стенда, конечно, зависимость была бы неидеальной и картина получилась бы более информативной с академической точки зрения.

5. 
   Используя значение длины волны для зеленой линии в таблице 4.2 расчитать методом переноса погрешностей постоянную дифракционной решетки .
   

Результаты заносим в табл. 4.2

Таблица 4.2 Константы эксперимента

Длина волны зеленого цвета λ=λ̅+Δλ̅ нм	Постоянная решетки d = d̅±Δd̅, мкм	Длина решетки L, см	Число щтрихов на решетке N=L/d̅
λ=546±5, нм с Р = 95%	5,92±0,18	2	3376

6. 
   Используя метод переноса погрешностей, рассчитать длины волн света, соответствующие желтому и синему участкам спектра. Результаты занести в таблицу 4.3.
   

---

Для примера показан расчёт для желтого участка спектра

7. 
   По экспериментальным данным трех таблиц по форме 4.1 и соотношению (4.5) определить угловую дисперсию дифракционной решетки для желтого, зеленого и синего участков спектра для . Результаты расчетов представить в таблице 4.3.
   

Для примера приведем расчёт для желтого участка спектра третьего порядка:

8. 
   Используя значение длины L и постоянной решетки (таблица 4.2), рассчитать число штрихов N на решетке. Результат расчета представить в таблице 4.2.
   

9. 
   По данным таблицы 4.2 рассчитать разрешающую способность R решетки для желтого, зеленого и синего участков спектра для . Результаты расчетов представить в таблице 4.3
   

Для примера приведем расчёт для желтого участка спектра третьего порядка:

10. 
    Рассчитать минимальный интервал длин волн двух близких спектральных линий, которые может разрешить данная решетка, для желтого, зеленого и синего участков спектра для . Результаты расчетов представить в таблице 4.3
    

Для примера приведем расчёт для желтого участка спектра третьего порядка:
Таблица 4.3 Определение длины волны и характеристик дифракционной решетки

Цвет спектральной линии	Угловой коэффициент a=a̅±Δa̅	Длина волны λ=λ̅+Δλ̅ нм	Порядок спектра, m	Dϕ=m/d̅cosϕm мин/нм	R=mN	Δλ=λ̅/R нм
Желтая	0,100±0,007	546±5	1	227,195	3376	175,3
			3	758,392	10129	58,4
Зеленая	0,092±0,003	591±4	1	169,528	3376	161,7
			3	508,671	10129	53,9
Синяя	0,078±0,002	462±1	1	169,340	3376	137,1
			3	507,966	10129	45,7

---

---

Смотрите также файлы

• Система методов оценки.docx

• Задание Какие страны достигли технологической зрелости к началу xx в., а какие власти в это же время встали на путь ускоренной индустриализации.docx

• Объект исследования Учебнотренировочный процесс стрелков армейской тактической стрельбы. Предмет исследования.pptx

• Ценностносмысловая позиция учителя Инструкция к выполнению практической работы 1.docx

• Тема Моральнонравственная характеристика деятельности прокурора в уголовном процессе.docx