№	y	x
1	20,48	124
2	20,13	96
3	20,26	106
4	19,89	70
5	19,92	97
6	19,78	76
7	20,23	112
8	20,46	113
9	20,07	109
10	20,23	91
11	20,26	95
12	20,28	115
13	20,52	114
14	20,28	133
15	19,97	116
16	19,97	85
17	19,57	91
18	19,94	82
19	20,29	105
20	20,83	124
21	19,59	70
22	19,76	84
23	20,19	106
24	20,66	128
25	19,95	105
26	20,61	121
27	20,03	79
28	19,78	82
29	20,22	80
30	19,78	37
31	20,09	101
32	20,13	98
33	20,56	98
34	20,51	134
35	19,71	39
36	20,1	88
37	20,32	108
38	20,37	112
39	20,03	80
40	20,65	120
41	20,19	88
42	20,24	104
43	20,27	94
44	20,69	107
45	19,85	82
46	19,87	84
47	20,2	101
48	20,33	98
49	20,2	99
50	20,46	118
51	20,17	90
52	20,62	123
53	19,79	107
54	20,34	97
55	20,51	126
56	20,04	147
57	20,39	88
58	20,27	111
59	20,06	121
60	20,39	104
61	19,94	63
62	19,95	99
63	20,23	114
64	20,49	99
65	20,61	94
66	20,56	124
67	20,42	117
68	19,73	64
69	19,42	52
70	20,17	114
71	19,87	78
72	20,26	85
73	20,04	57
74	20,34	98
75	20,63	119
76	20,32	94
77	20,06	94
78	20,04	83
79	20,62	118
80	20,53	116

---

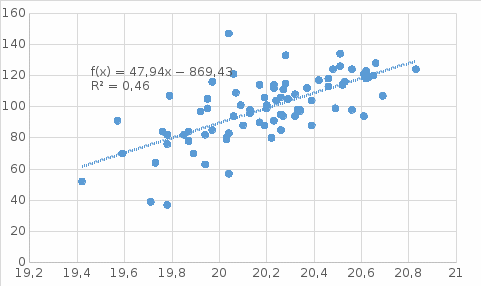
Уравнение регрессии (эмпирическое уравнение регрессии):y = 47.941 x - 869.43Х- Дивиденды, начисленные по результатам деятельностиУ – Курсовая цена акции, рубТест Голдфелда-Квандта.В данном случае предполагается, что стандартное отклонение σi = σ(εi) пропорционально значению yi переменной Y в этом наблюдении, т.е. σ2i = σ2y2i , i = 1,2,…,n.Тест Голдфелда-Квандта состоит в следующем:1. Все n наблюдений упорядочиваются по величине Y.2. Вся упорядоченная выборка после этого разбивается на три подвыборки размерностей k,(n-2k),k.3. Оцениваются отдельные регрессии для первой подвыборки (k первых наблюдений) и для третьей подвыборки (k последних наблюдений).4. Для сравнения соответствующих дисперсий строится соответствующая F-статистика:F = S3/S1Построенная F-статистика имеет распределение Фишера с числом степеней свободы v1 = v2 = (n – c - 2m)/2.5. Если F > Fkp, то гипотеза об отсутствии гетероскедастичности отклоняется.Этот же тест может использоваться при предположении об обратной пропорциональности между σi и значениями объясняющей переменной. При этом статистика Фишера имеет вид:F = S1/S31. Упорядочим все значения по величине Y.2. Находим размер подвыборки k = (80 - 21)/2 = 30.где c = 4n/15 = 4*80/15 = 213. Оценим регрессию для первой подвыборки.Находим параметры уравнения методом наименьших квадратов.Система уравнений МНК:a0n + a1∑y = ∑xa0∑y + a1∑y2 = ∑x•yДля наших данных система уравнений имеет вид:30a0 + 596.49a1 = 2534596.49a0 + 11860.81a1 = 50440.01Из первого уравнения выражаем а0 и подставим во второе уравнениеПолучаем a0 = 70.77, a1 = -1322.59

y	x	y2	x2	y*x	x(y)	(x-x(y))2
19.42	52	377.136	2704	1009.84	51.702	0.089
19.57	91	382.985	8281	1780.87	62.317	822.73
19.59	70	383.768	4900	1371.3	63.732	39.287
19.71	39	388.484	1521	768.69	72.224	1103.837
19.73	64	389.273	4096	1262.72	73.639	92.918
19.76	84	390.458	7056	1659.84	75.762	67.858
19.78	76	391.248	5776	1503.28	77.178	1.387
19.78	82	391.248	6724	1621.96	77.178	23.254
19.78	37	391.248	1369	731.86	77.178	1614.248
19.79	107	391.644	11449	2117.53	77.885	847.661
19.85	82	394.023	6724	1627.7	82.131	0.0173
19.87	84	394.817	7056	1669.08	83.547	0.205
19.87	78	394.817	6084	1549.86	83.547	30.766
19.89	70	395.612	4900	1392.3	84.962	223.862
19.92	97	396.806	9409	1932.24	87.085	98.307
19.94	82	397.604	6724	1635.08	88.5	42.255
19.94	63	397.604	3969	1256.22	88.5	650.268
19.95	105	398.003	11025	2094.75	89.208	249.386
19.95	99	398.003	9801	1975.05	89.208	95.883
19.97	116	398.801	13456	2316.52	90.623	643.974
19.97	85	398.801	7225	1697.45	90.623	31.622
20.03	79	401.201	6241	1582.37	94.869	251.836
20.03	80	401.201	6400	1602.4	94.869	221.098
20.04	147	401.602	21609	2945.88	95.577	2644.323
20.04	57	401.602	3249	1142.28	95.577	1488.186
20.04	83	401.602	6889	1663.32	95.577	158.181
20.06	121	402.404	14641	2427.26	96.992	576.367
20.06	94	402.404	8836	1885.64	96.992	8.954
20.07	109	402.805	11881	2187.63	97.7	127.69
20.09	101	403.608	10201	2029.09	99.115	3.552
596.49	2534	11860.809	230196	50440.01	2534	12160.005

---

Здесь S1 = 12160Оценим регрессию для третьей подвыборки.Находим параметры уравнения методом наименьших квадратов.Система уравнений МНК:a0n + a1∑y = ∑xa0∑y + a1∑y2 = ∑x•yДля наших данных система уравнений имеет вид:30a0 + 614.79a1 = 3374614.79a0 + 12599.45a1 = 69163.17Из первого уравнения выражаем а0 и подставим во второе уравнениеПолучаем a0 = 35.41, a1 = -613.18

x	y	x2	y2	x*y	y(x)	(y-y(x))2
20.28	133	411.278	17689	2697.24	104.924	788.239
20.29	105	411.684	11025	2130.45	105.278	0.0776
20.32	108	412.902	11664	2194.56	106.341	2.753
20.32	94	412.902	8836	1910.08	106.341	152.295
20.33	98	413.309	9604	1992.34	106.695	75.601
20.34	97	413.716	9409	1972.98	107.049	100.982
20.34	98	413.716	9604	1993.32	107.049	81.884
20.37	112	414.937	12544	2281.44	108.111	15.122
20.39	88	415.752	7744	1794.32	108.819	433.45
20.39	104	415.752	10816	2120.56	108.819	23.227
20.42	117	416.976	13689	2389.14	109.882	50.669
20.46	113	418.612	12769	2311.98	111.298	2.896
20.46	118	418.612	13924	2414.28	111.298	44.915
20.48	124	419.43	15376	2539.52	112.006	143.848
20.49	99	419.84	9801	2028.51	112.36	178.501
20.51	134	420.66	17956	2748.34	113.069	438.122
20.51	126	420.66	15876	2584.26	113.069	167.22
20.52	114	421.07	12996	2339.28	113.423	0.333
20.53	116	421.481	13456	2381.48	113.777	4.943
20.56	98	422.714	9604	2014.88	114.839	283.556
20.56	124	422.714	15376	2549.44	114.839	83.922
20.61	121	424.772	14641	2493.81	116.61	19.276
20.61	94	424.772	8836	1937.34	116.61	511.194
20.62	123	425.184	15129	2536.26	116.964	36.437
20.62	118	425.184	13924	2433.16	116.964	1.074
20.63	119	425.597	14161	2454.97	117.318	2.83
20.65	120	426.423	14400	2478	118.026	3.897
20.66	128	426.836	16384	2644.48	118.38	92.543
20.69	107	428.076	11449	2213.83	119.442	154.813
20.83	124	433.889	15376	2582.92	124.4	0.16
614.79	3374	12599.45	384058	69163.17	3374	3894.78

---

Здесь S3 = 3894.78Число степеней свободы v1 = v2 = (n – c - 2m)/2 = (80 - 21 - 2*1)/2 = 28.5Fkp(28.5,28.5) = 4.2Строим обратную F-статистику:F = 12160/3894.78 = 3.12Поскольку F < Fkp = 4.2, то гипотеза об отсутствии гетероскедастичности принимается.

---

Смотрите также файлы

• Разработка продуктовой стратегии предприятия.docx

• Лабораторная работа 3 По дисциплине Техника высоких напряжений 6В07101 Электроэнергетика На тему Генератор импульсных напряжений (гин).docx

• Тема Стремление к знаниям, трудолюбие и патриотизм.docx

• Задание для практической работы по модулю Государственная символика Российской Федерации Класс 5 Цель.docx

• Решение р s (1 nd).doc