Файл: Решение. Задание Вычислить произведение матриц а и В, если Решение.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 40
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 1. Найти матрицу С, равную сумме матриц А и В, если
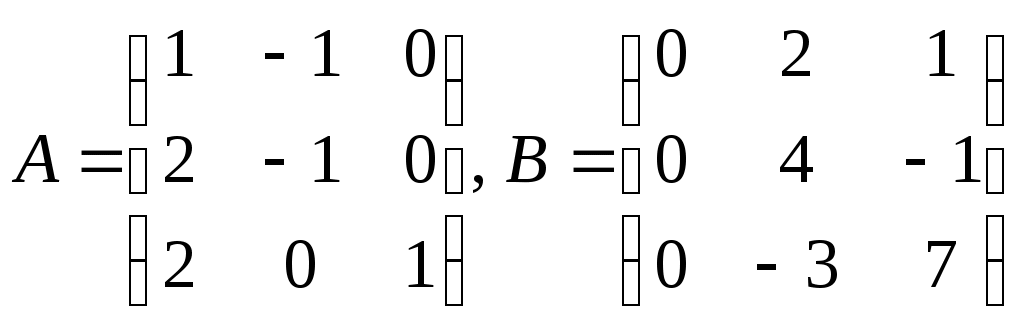
Решение.
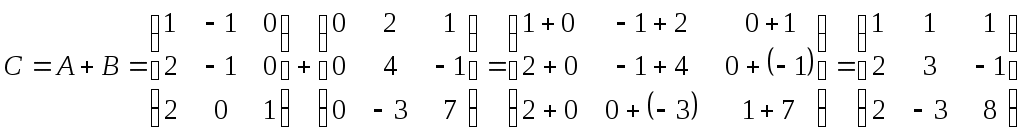
Задание 2. Вычислить произведение матриц А и В, если
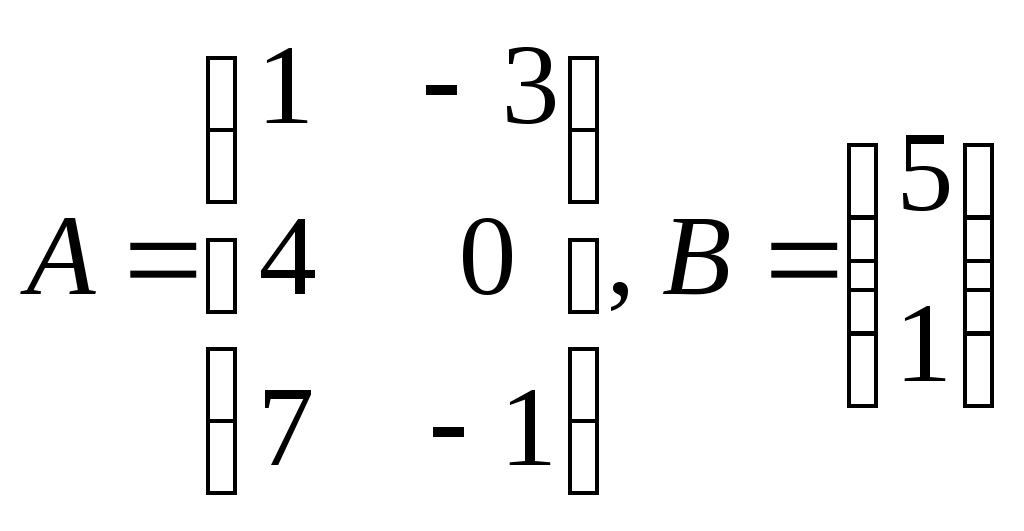
Решение.
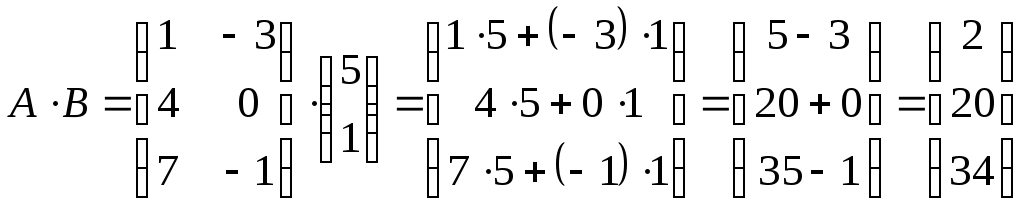
Задание 3. Вычислить произведение матриц А и В, если
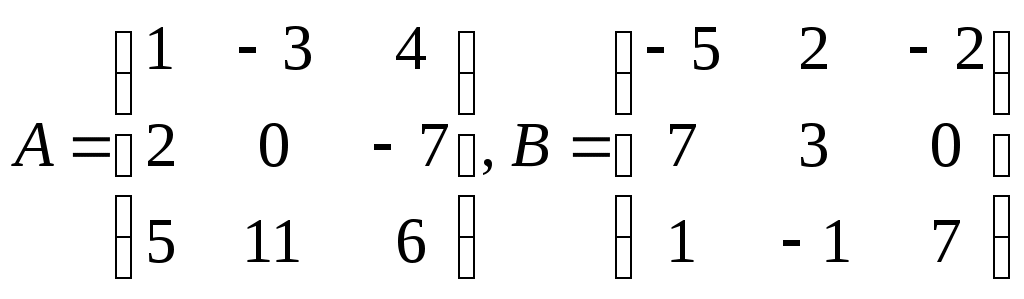
Решение.
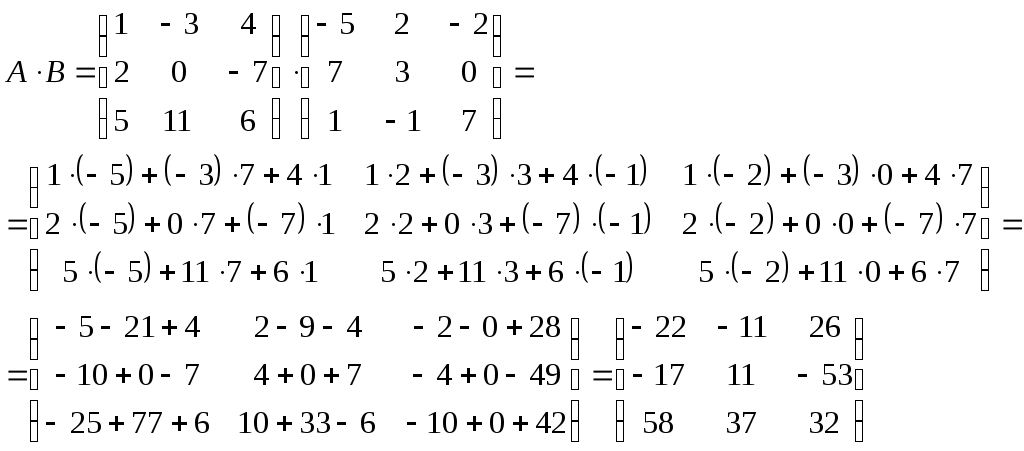
Задание 4. Найти матрицу, обратную к матрице А
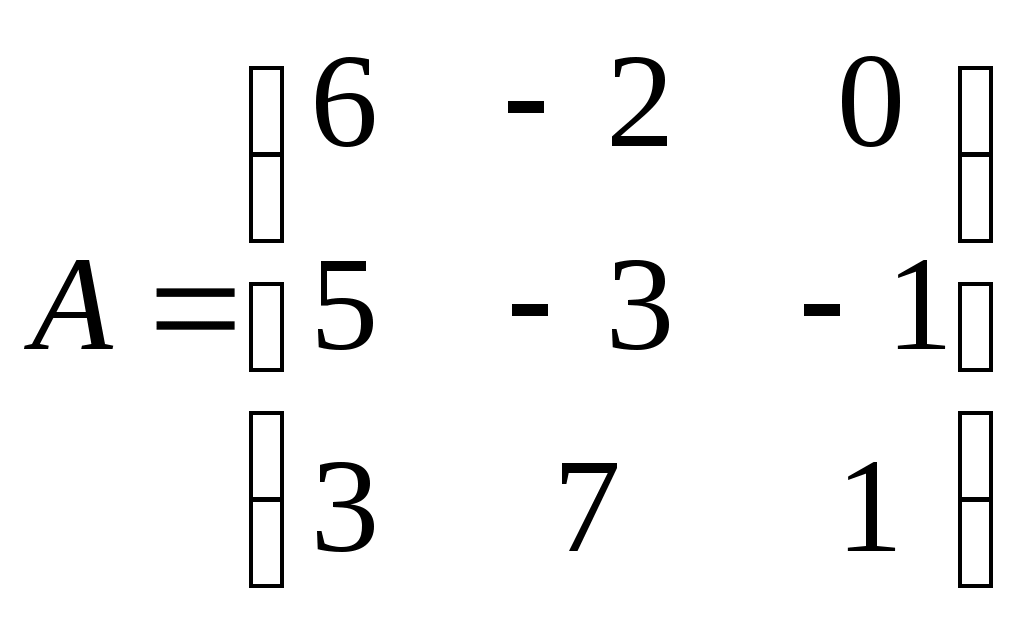
Решение.
Найдем определитель матрицы А:
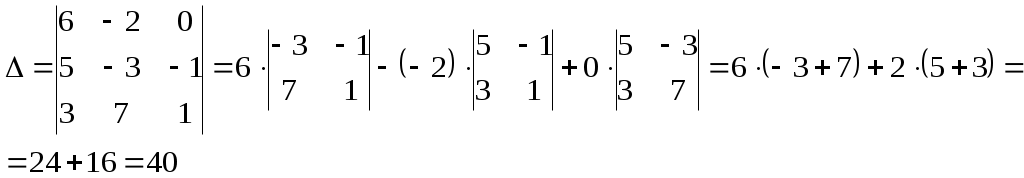
Найдем алгебраические дополнения для всех элементов матрицы А:
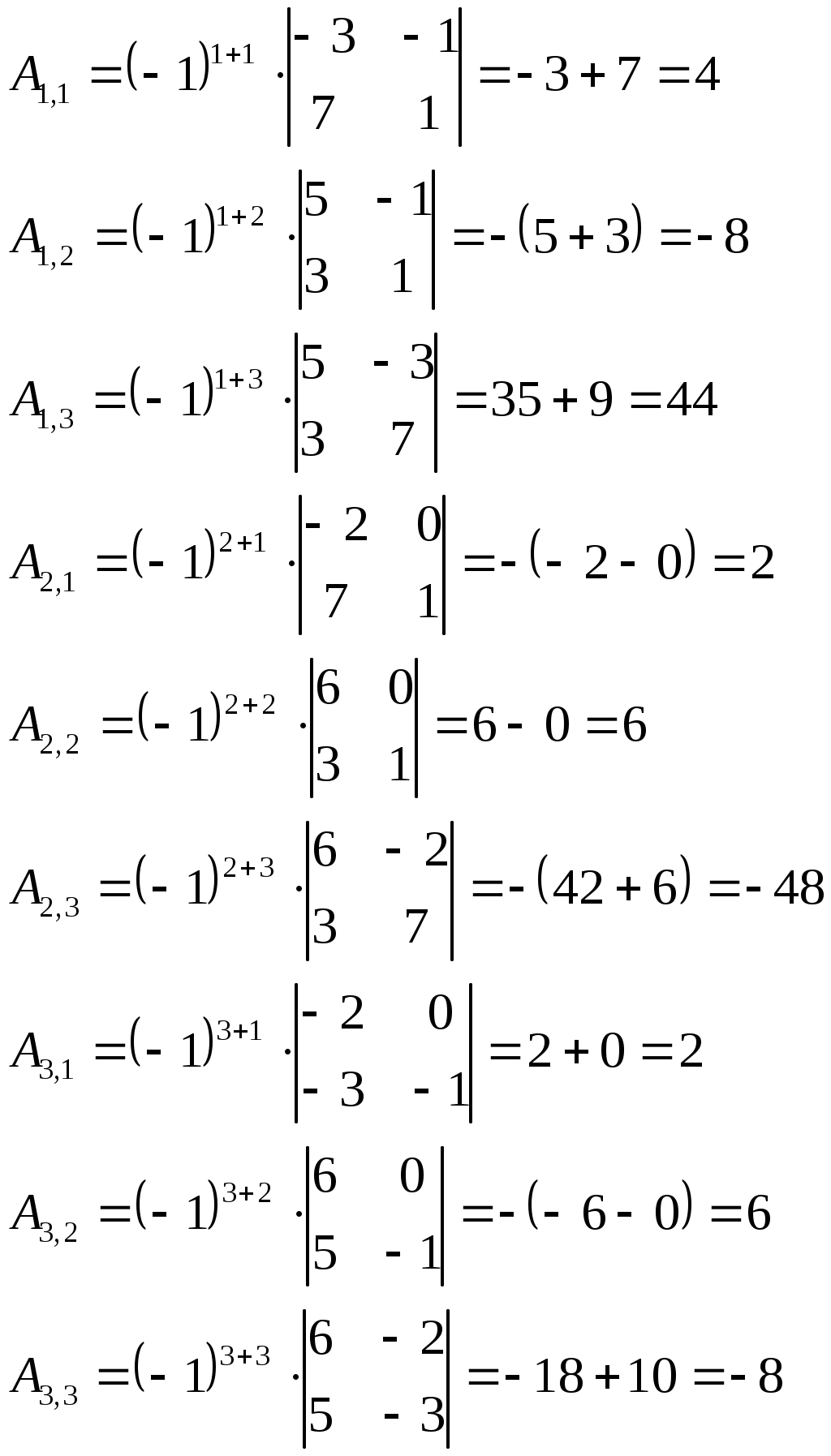
Составим матрицу алгебраических дополнений:
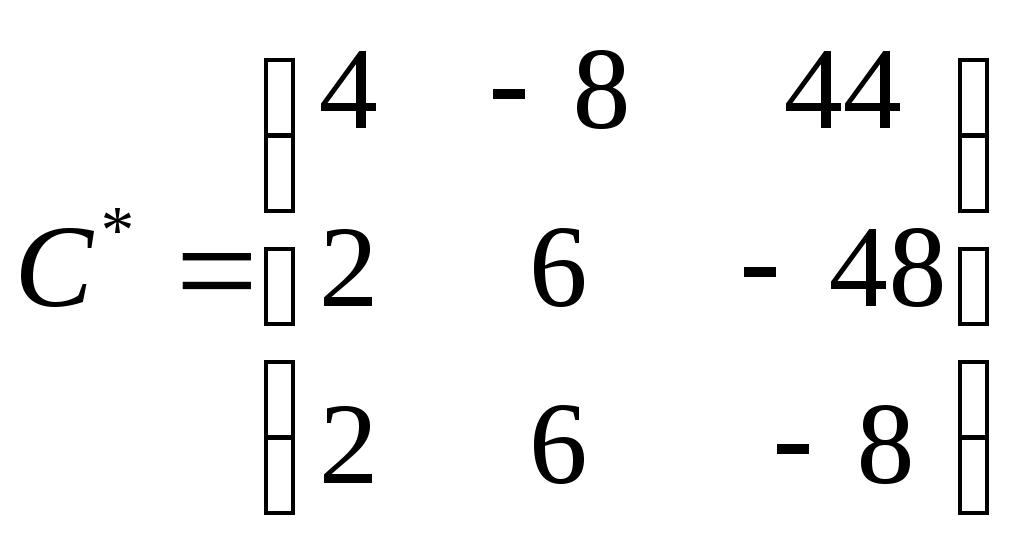
Транспонируем полученную матрицу:
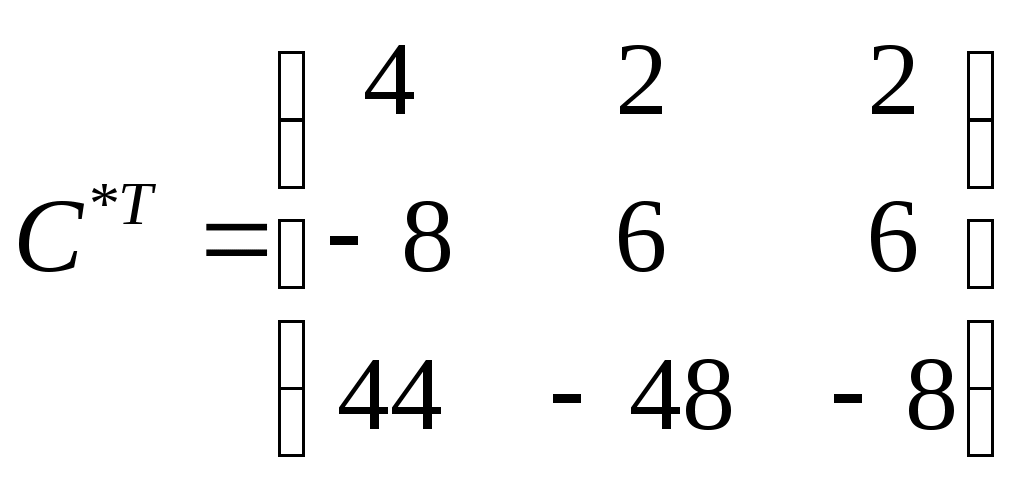
Найдем обратную матрицу:
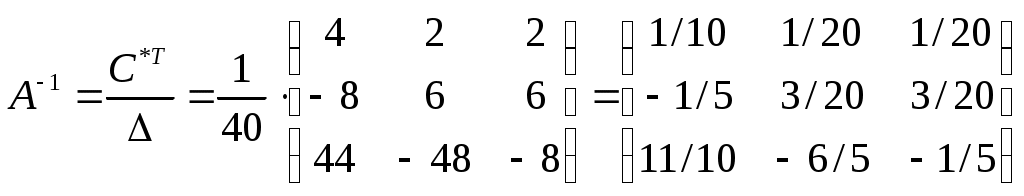
Задание 5. Решить систему матричным методом
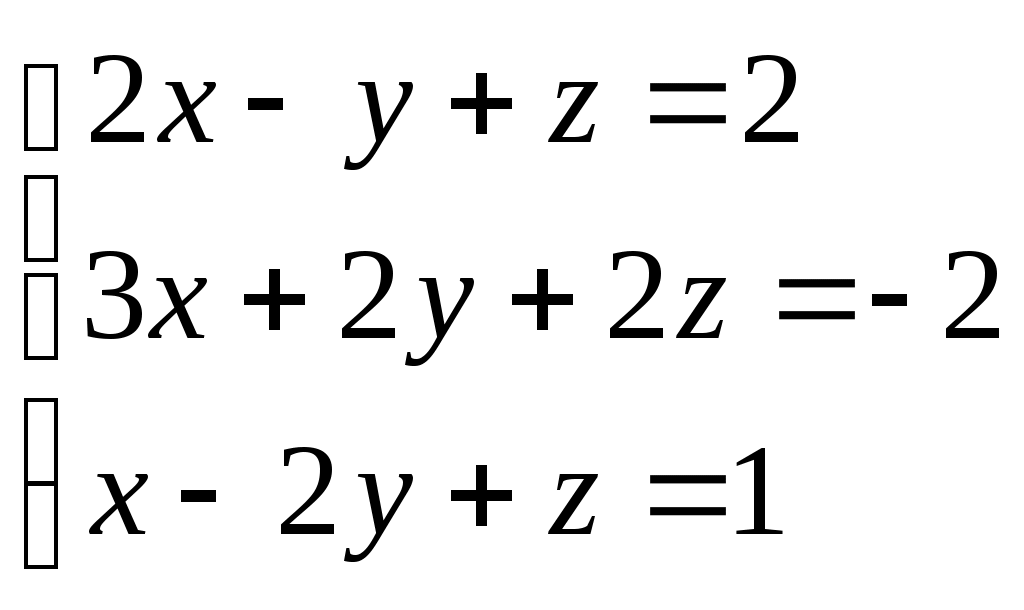
Решение.
Система уравнений в общем виде:
, гдеА – матрица, составленная из коэффициентов при неизвестных
В – столбец свободных членов.
Решение системы в общем виде:
Найдем А–1 – матрицу, обратную матрице А.
Найдем определитель матрицы А:
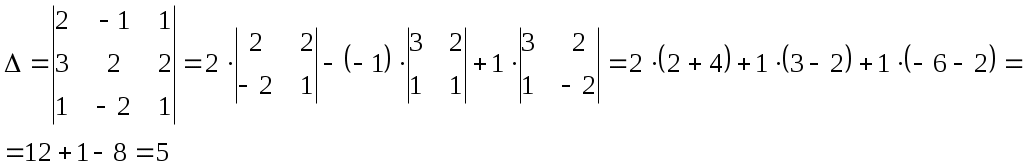
Найдем алгебраические дополнения для всех элементов матрицы А:
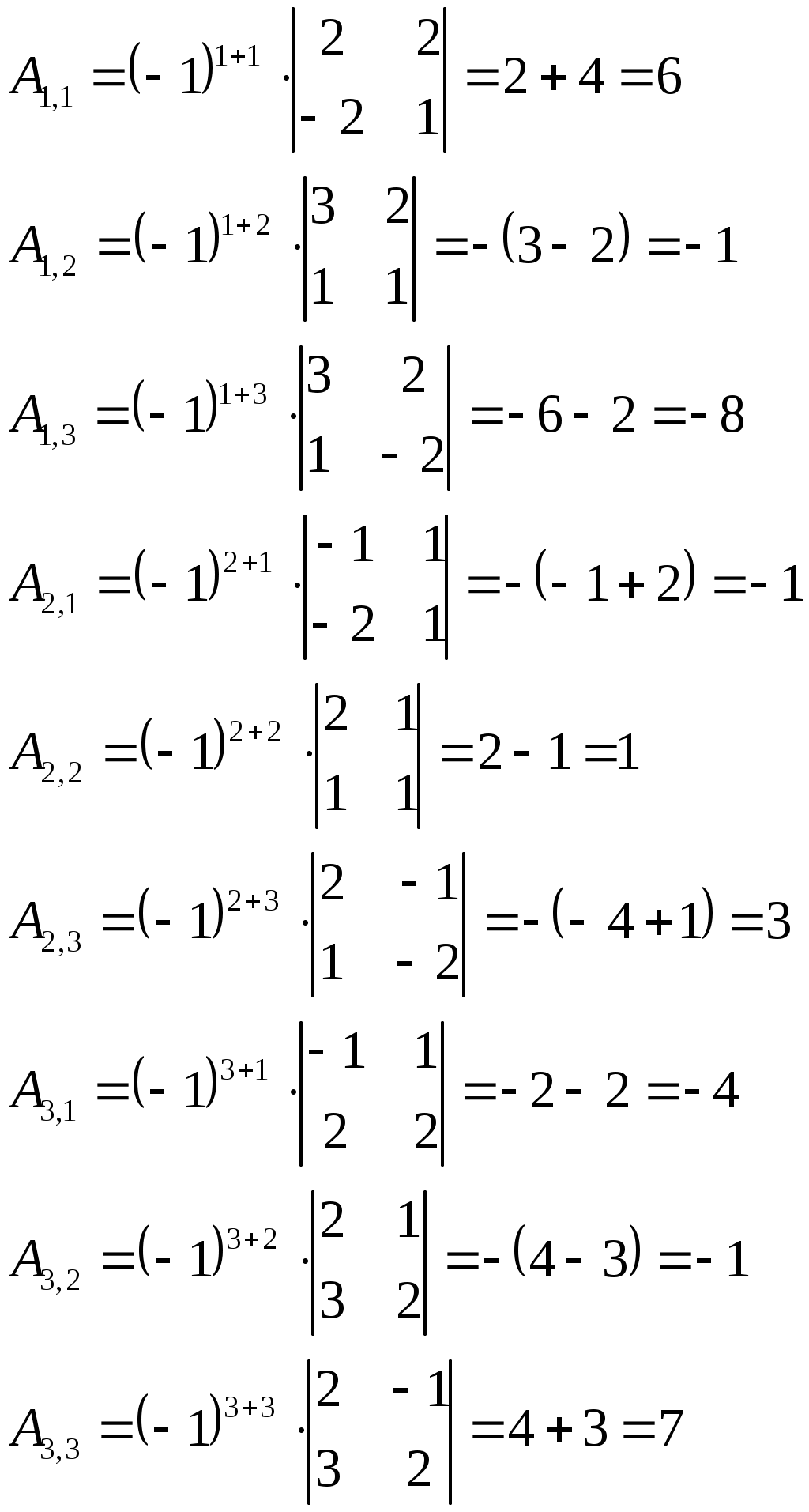
Составим матрицу алгебраических дополнений:
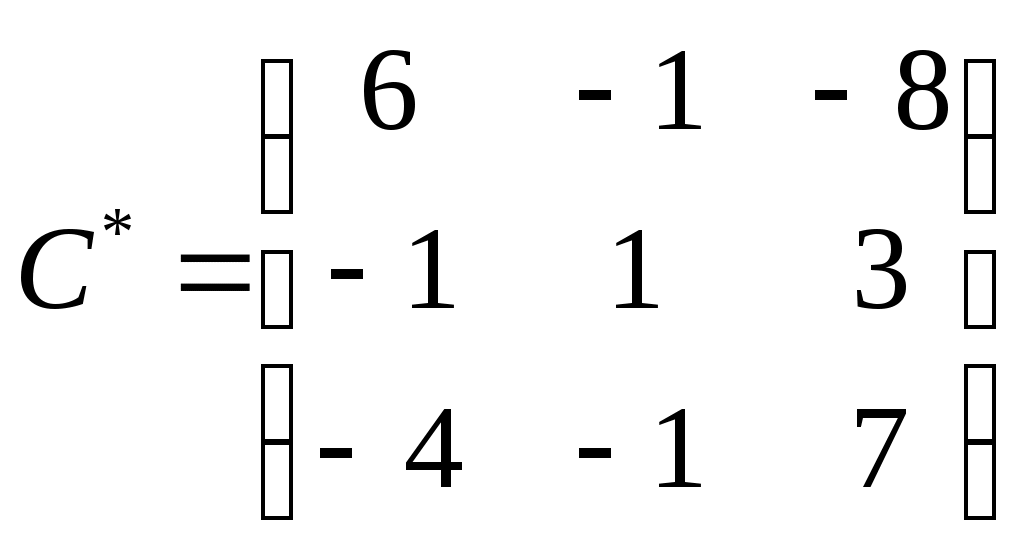
Транспонируем полученную матрицу:
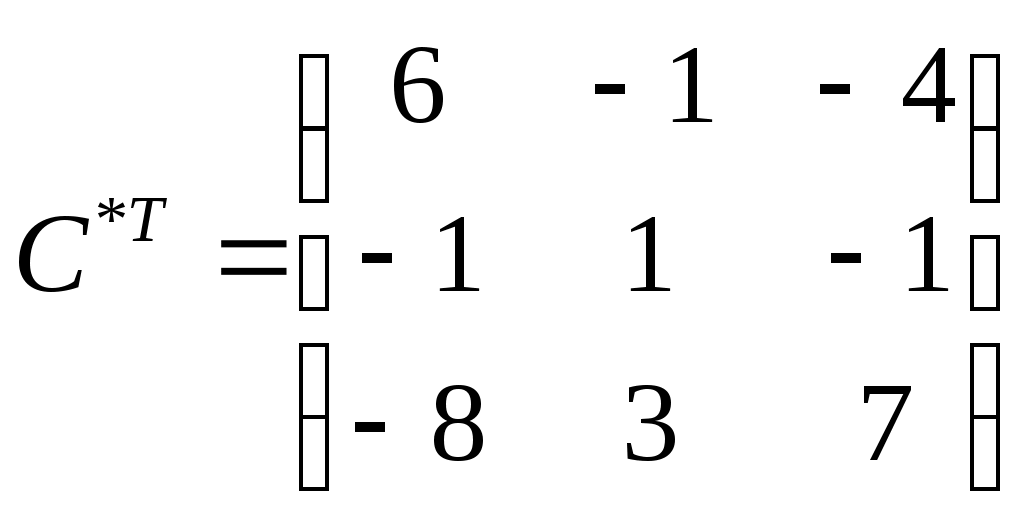
Найдем обратную матрицу:
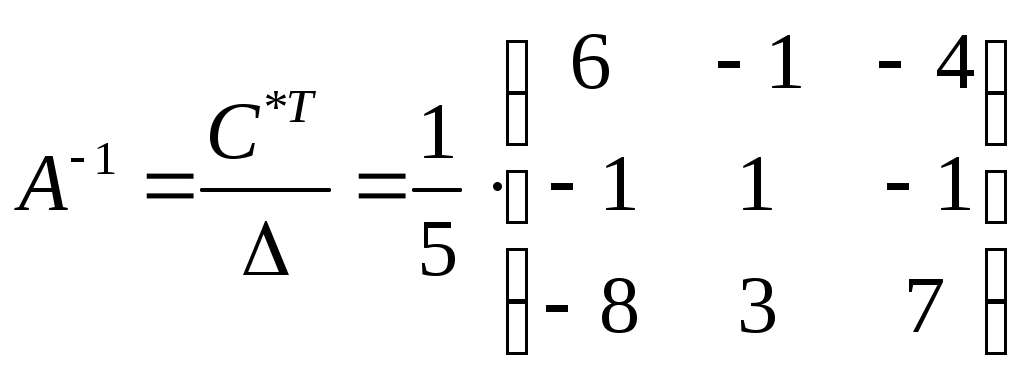
Найдем решение системы уравнений:
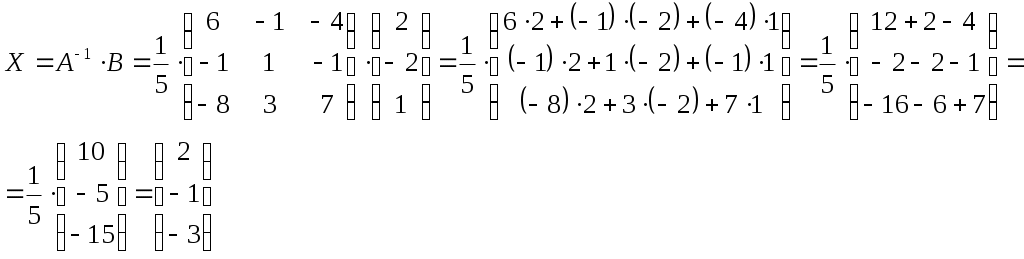
Получили решение системы уравнений:
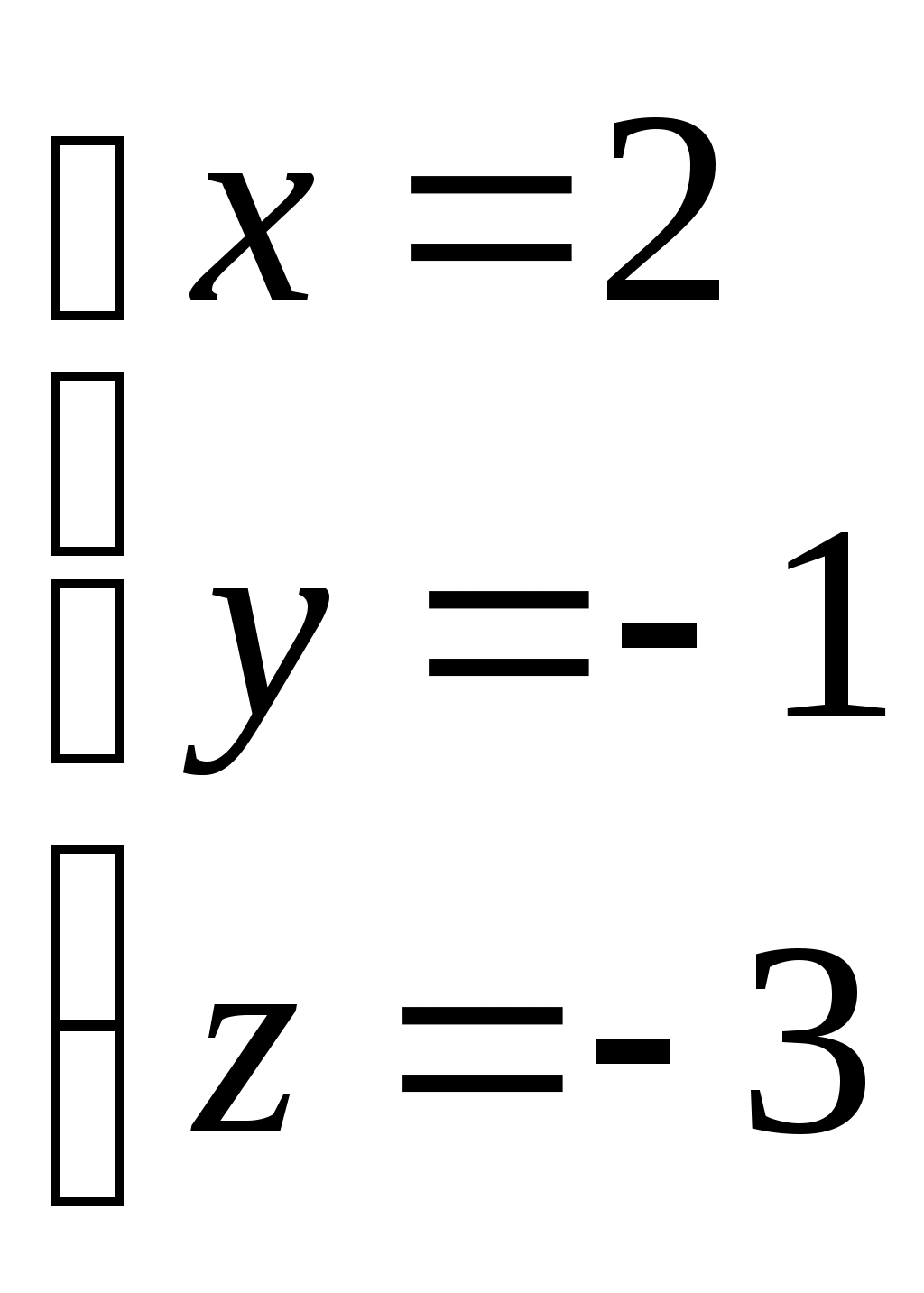
Задание 6. Решить систему методом Гаусса
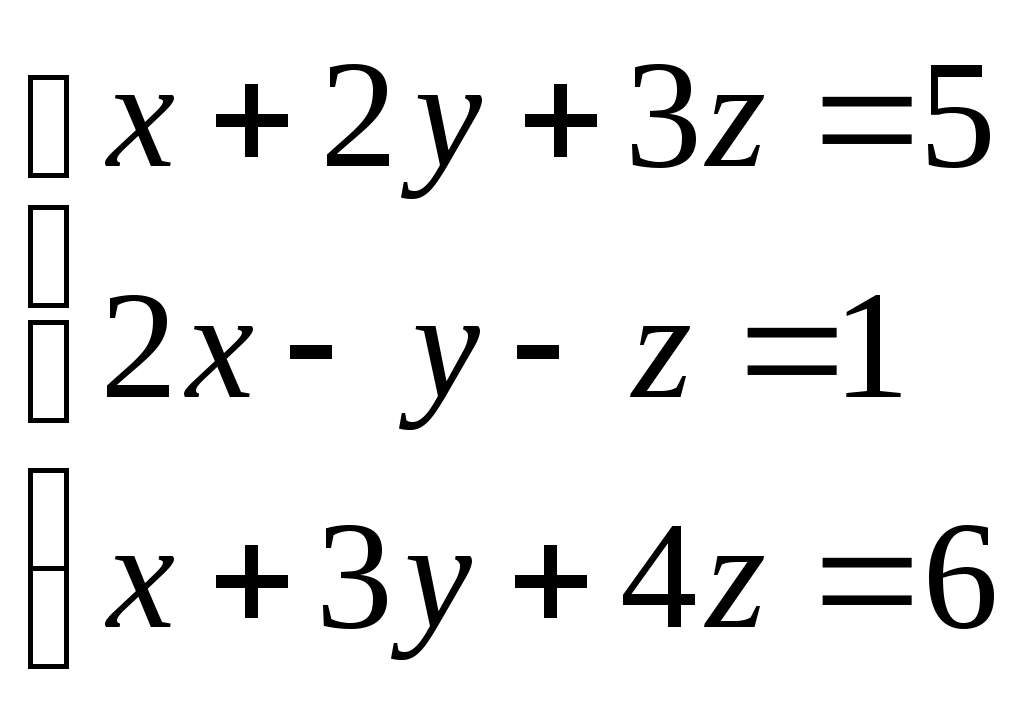
Решение.
Представим систему в матричном виде:
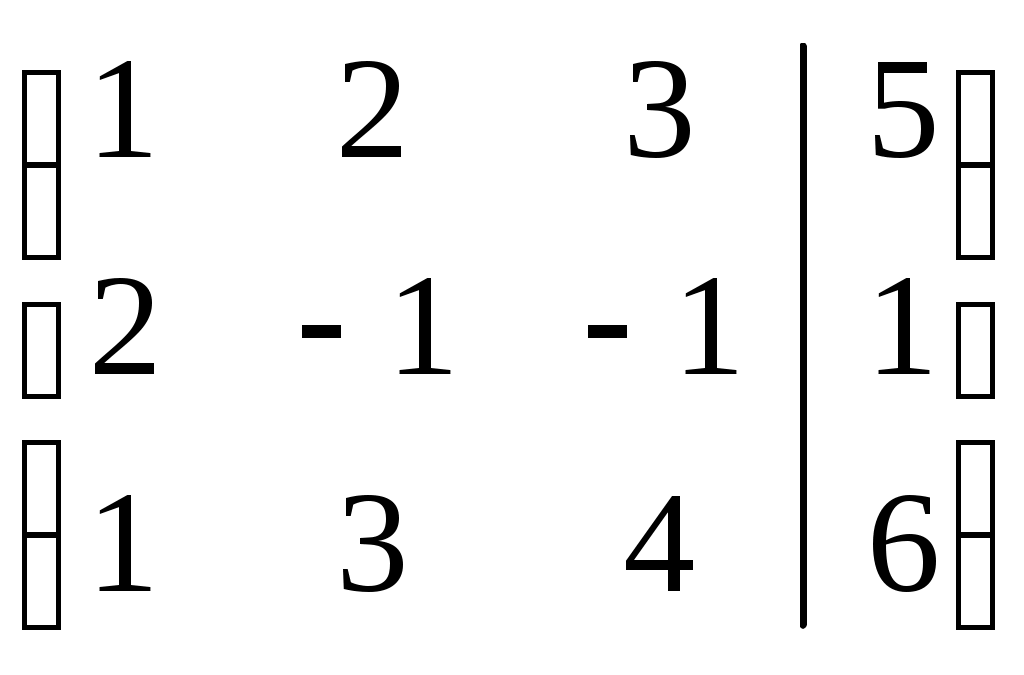
Вычтем из 2-ой строки 1-ую строку, умноженную на 2. Получим:
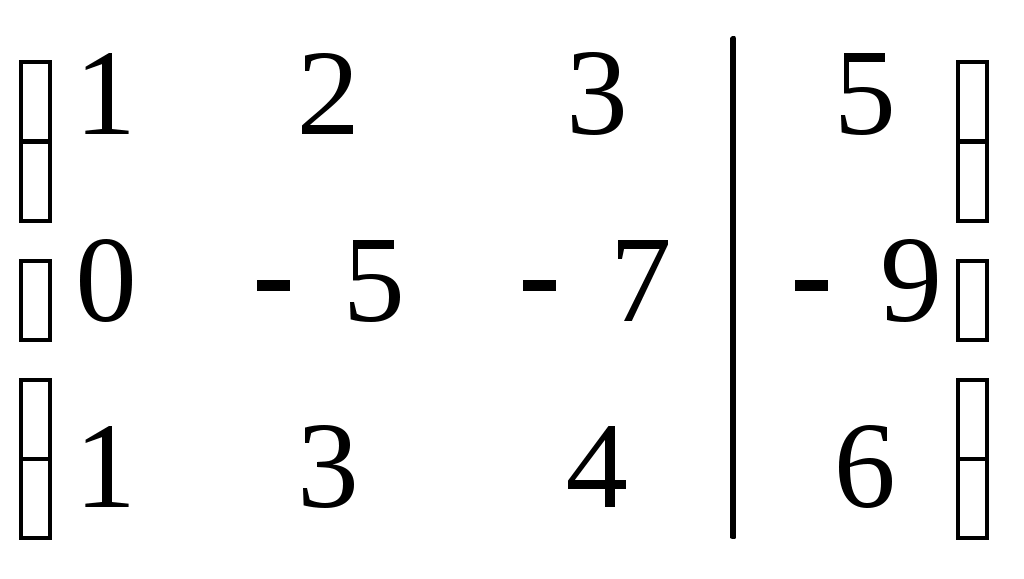
Вычтем из 3-ей строки 1-ую строку. Получим:
Разделим 2-ую строку на (–5). Получим:
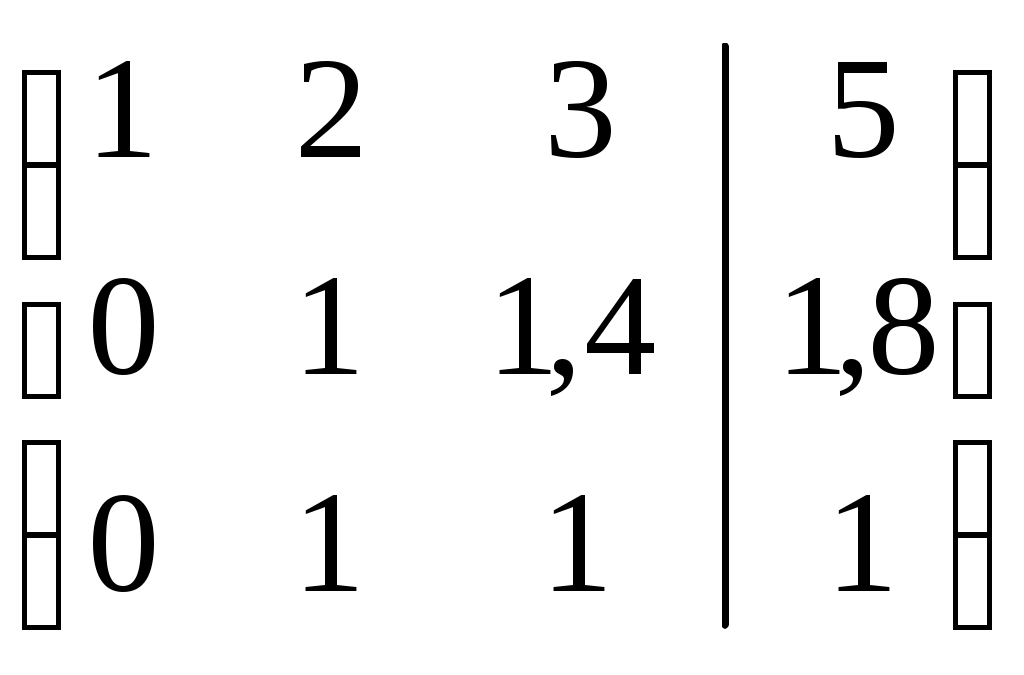
Вычтем из 1-ой строки 2-ую строку, умноженную на 2. Получим:
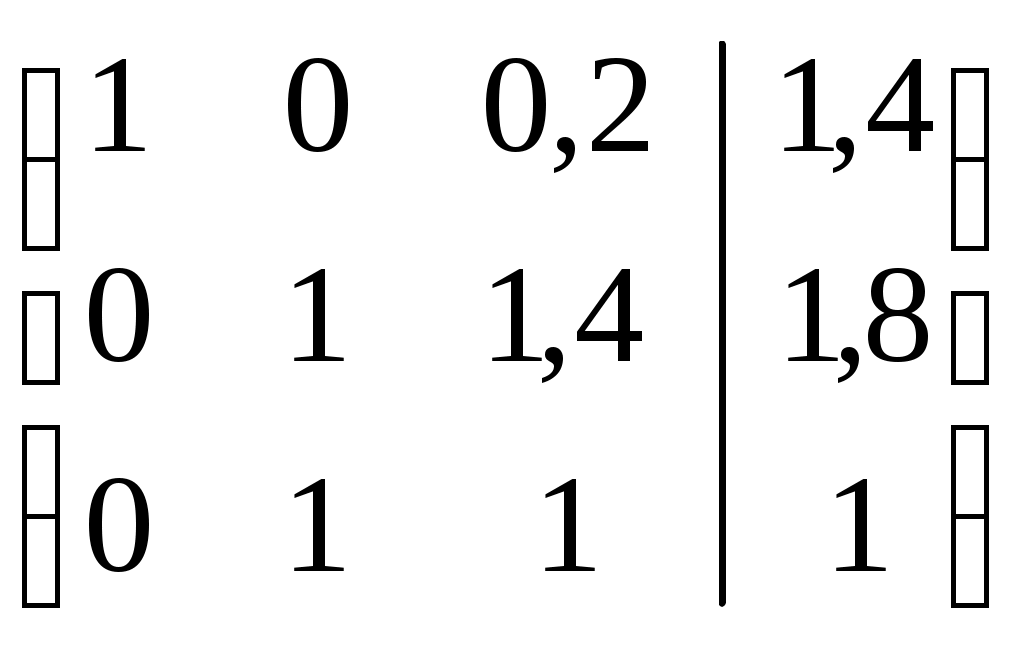
Вычтем из 3-ей строки 2-ую строку. Получим:
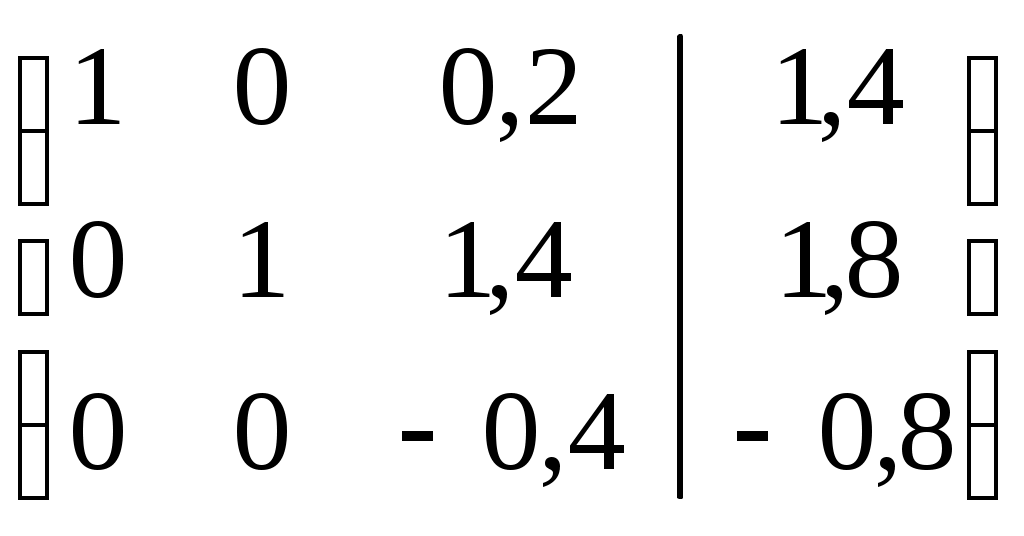
Разделим 3-ю строку на (–0,4). Получим:
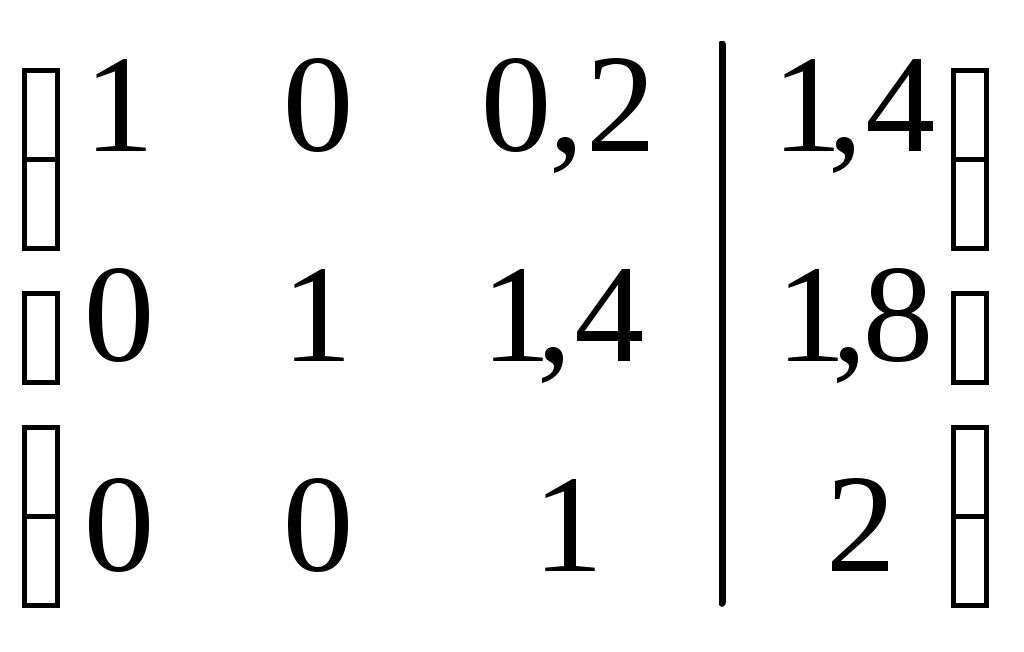
Вычтем из 1-ой строки 3-ю строку, умноженную на 0,2. Получим:
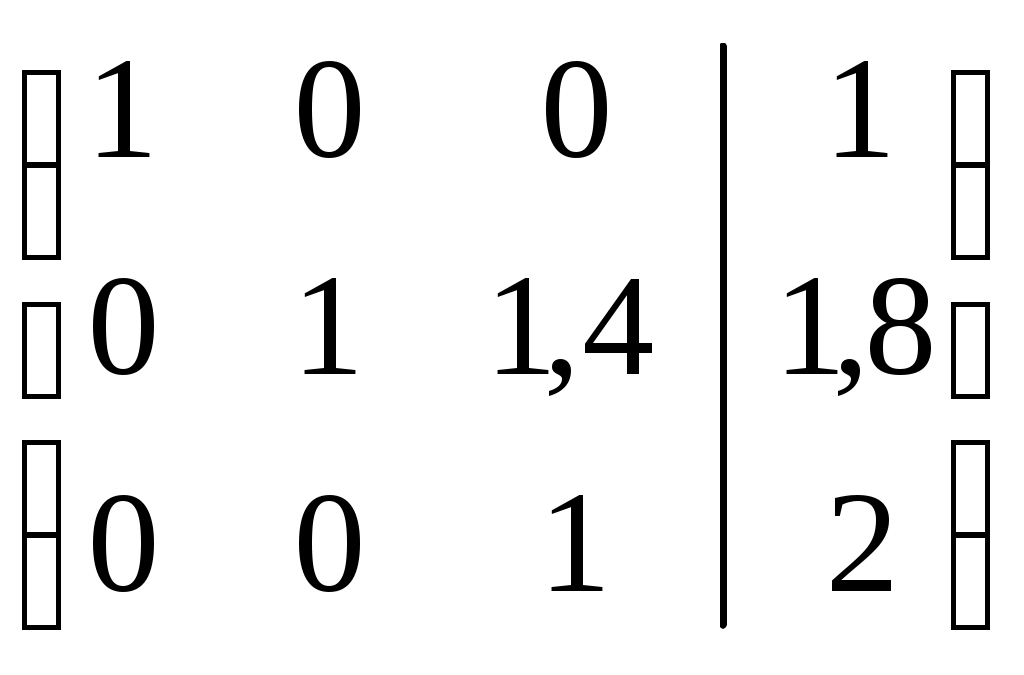
Вычтем из 2-ой строки 3-ю строку, умноженную на 1,4. Получим:
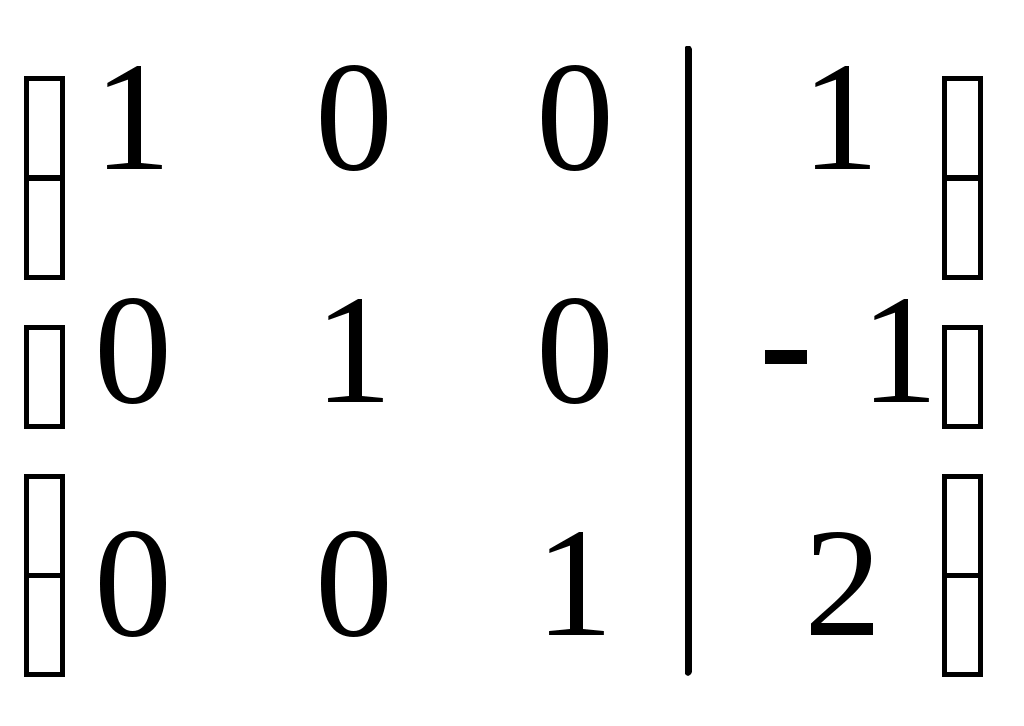
Получили решение системы уравнений:
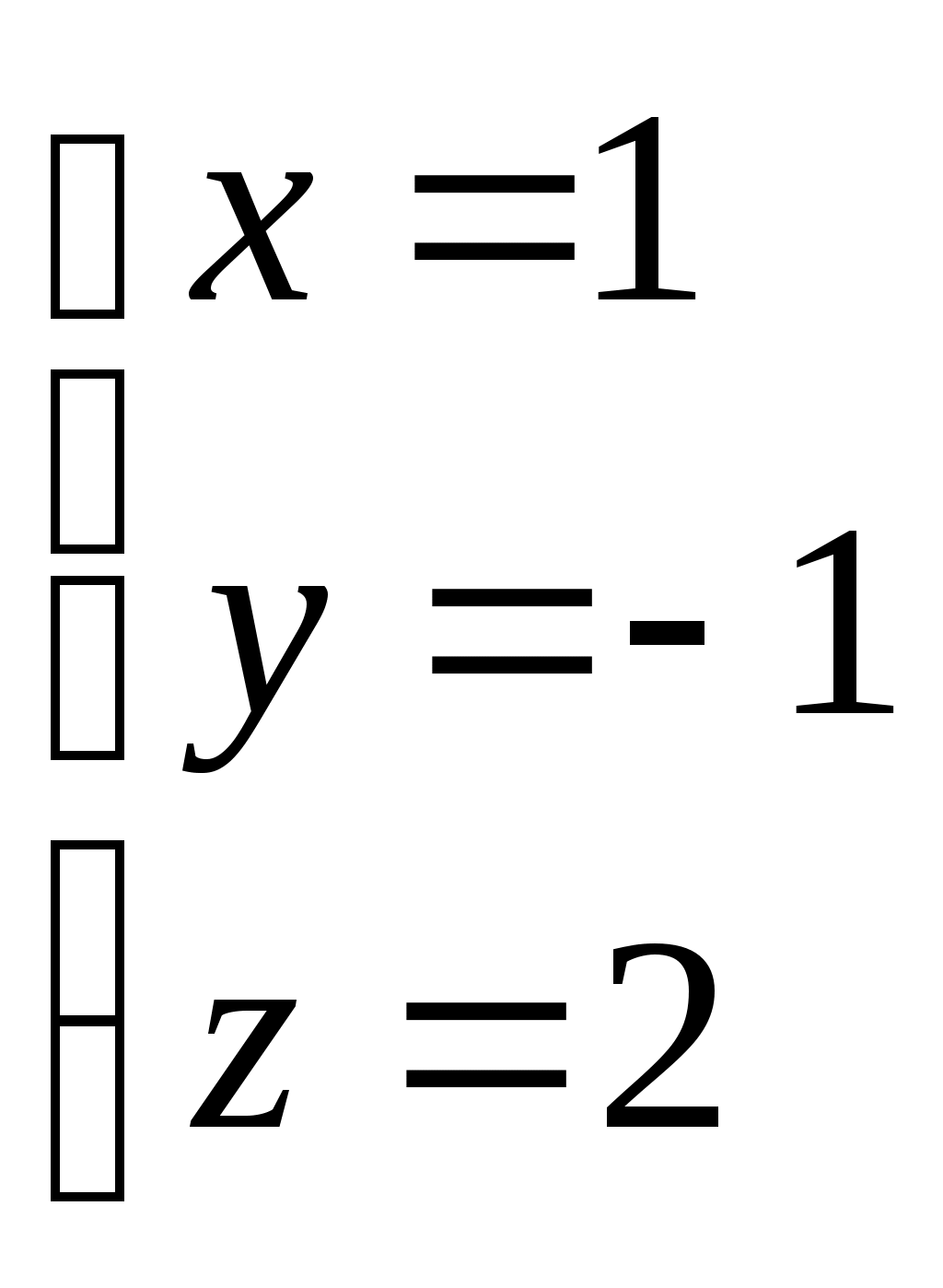
Задание 7. Решить систему методом Крамера
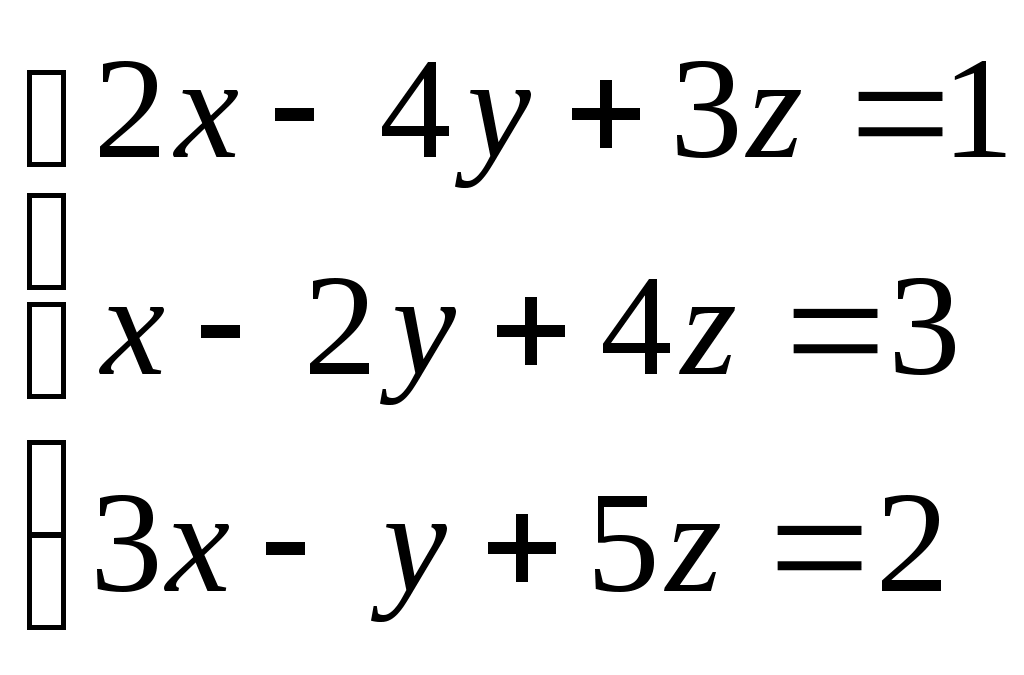
Решение.
Найдем главный определитель матрицы, составленной из коэффициентов при неизвестных:
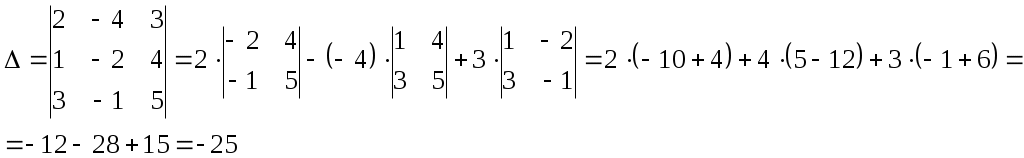
Найдем 1-ый определитель матрицы. Для этого вместо 1-го столбца подставим столбец свободных членов:
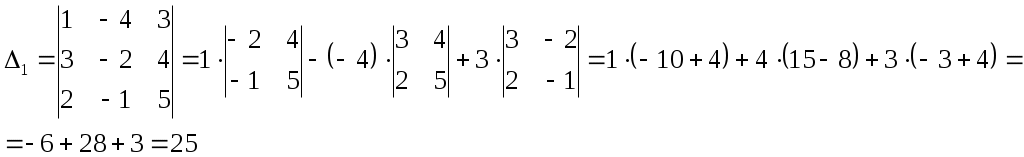
Найдем 2-ой определитель матрицы. Для этого вместо 2-го столбца подставим столбец свободных членов:
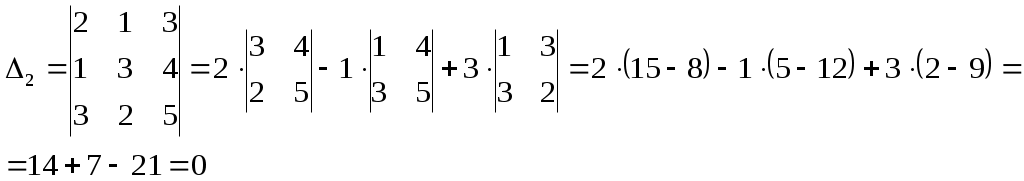
Найдем 3-ий определитель матрицы. Для этого вместо 3-го столбца подставим столбец свободных членов:
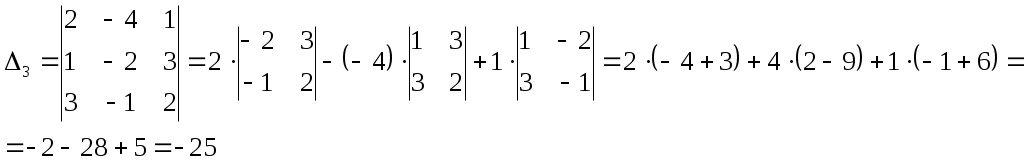
Получили решение системы уравнений:
Задание 8. Фирмой было выделено 236 тыс. усл. ед. для покупки 29 предметов для оборудования офиса: несколько компьютеров по цене 20 тыс. усл. ед. за компьютер, офисных столов по 8,5 тыс. усл. ед. за стол, стульев по 1,5 тыс. усл. ед. за стул. Позже выяснилось, что в другом месте компьютеры можно приобрести по 19,5 тыс. усл. ед., а столы – по 8 тыс. усл. ед. (стулья по той же цене), благодаря чему на ту же сумму было куплено на 1 стол больше. Выяснить, какое количество единиц каждого вида оборудования было приобретено.
Решение.
Пусть х – количество компьютеров, у – количество столов, (29 – х – у) – количество стульев. Тогда получим систему уравнений:
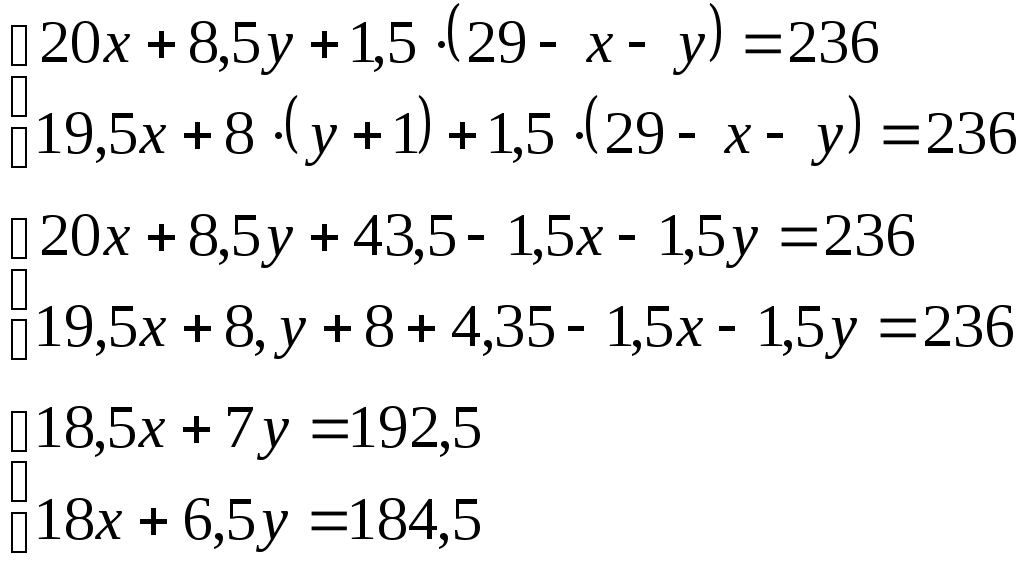
Решим полученную систему уравнений методом Крамера:
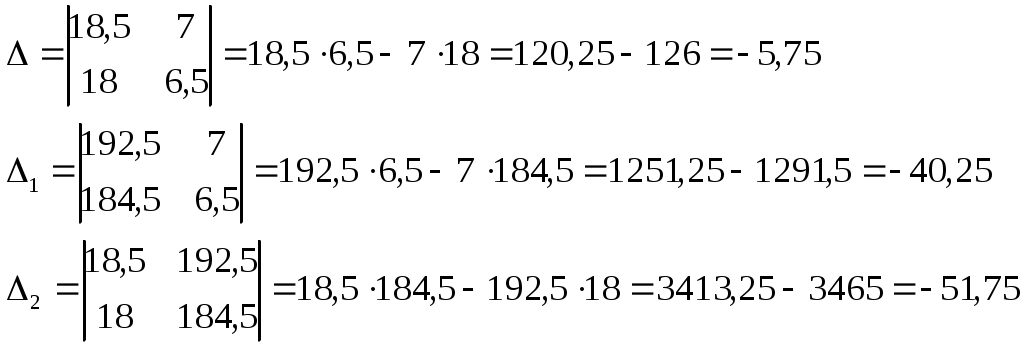
Отсюда:
Получили:
– 7 компьютеров;
– 9 столов;
– (29 – 7 – 9) = 13 стульев.
Так как в условии сказано, что приобрели на 1 стол больше, следовательно:
компьютеров – 7, столов – 10, стульев – 13.
Задание 9. Объемы трех видов продукции, выпущенных фирмой «Пласт» за декабрь прошедшего года задаются вектором
, цена каждого из выпускаемых товаров (в рублях) задается вектором 
. Определить стоимость продукции, выпущенной фирмой «Пласт» за декабрь прошедшего года.
Решение.
Чтобы найти стоимость продукции, необходимо найти скалярное произведение векторов
и 
.
Задание 10. Найти площадь параллелограмма, построенного на векторах пространства
и 
. Ответ округлить с точностью до десятых.Решение.
Найдем векторное произведение векторов:
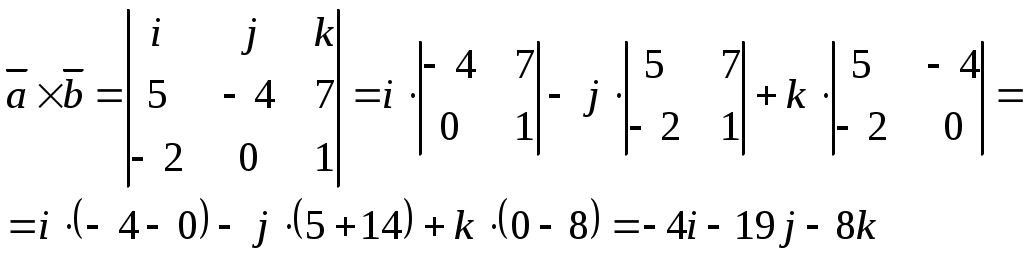
Найдем модуль векторного произведения, который является площадью параллелограмма:
Задание 11. Составить каноническое уравнение прямой, проходящей через точку М0 (–1; 2; 4), перпендикулярно вектору
Решение.
Уравнение прямой найдем по формуле:
x0, y0, z0 – координаты точки
А, В, С – координаты вектора
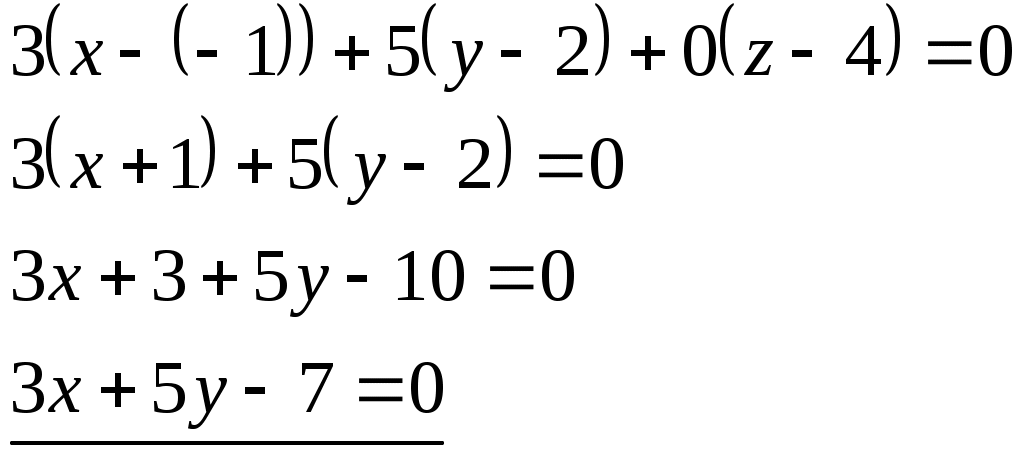
Задание 12. В треугольнике с вершинами А(–2; 0), В(2; 6) и С(4; 2) проведена медиана ВЕ. Написать уравнение медианы ВЕ.
Решение.
Медиана ВЕ делит сторону АС пополам. Найдем координаты точки Е – середины стороны АС:
Составим уравнение прямой ВЕ по точкам В(2; 6) и Е(1; 1):
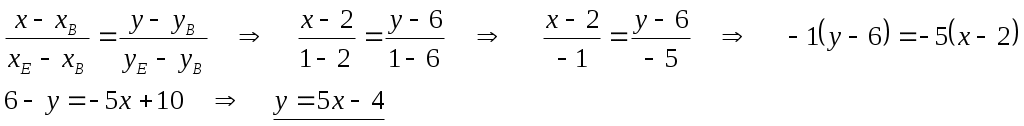
Задание 13. Составить уравнение плоскости, проходящей через точки
А(–3; 2; 1) и В(4; –1; 2) перпендикулярно плоскости
Решение.
Нормаль заданной плоскости
будет перпендикулярна самой плоскости и параллельна плоскости, которую необходимо найти.
Возьмем произвольную точку М(х; у; z). Тогда условие компланарности векторов задает требуемое уравнение плоскости:
– смешанное произведение трех векторов.
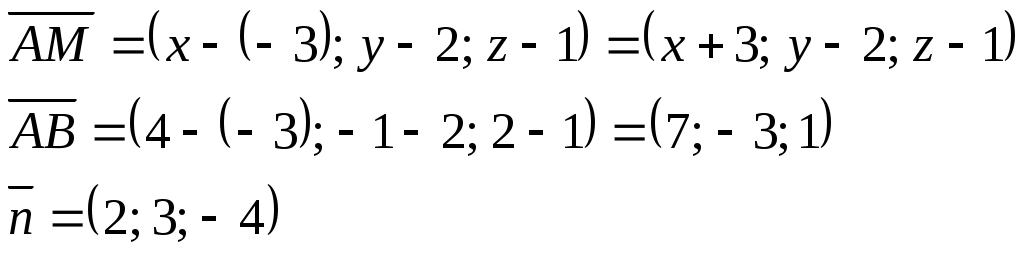
Найдем смешанное произведение трех векторов и приравняем его нулю, тем самым получим требуемое уравнение плоскости:
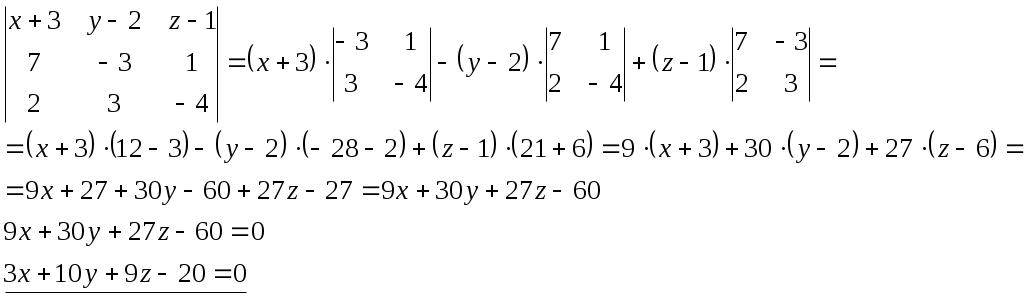
Задание 14. Написать уравнение эллипса, если известно, что расстояние между фокусами равно 8, а малая полуось b = 3
Решение.
Уравнение эллипса в общем виде:
Параметр b = 3, необходимой найти параметр а.
Расстояние между фокусами:
Найдем параметр а из соотношения:
Следовательно, уравнение эллипса:
Задание 15. Найти эксцентриситет гиперболы, заданной уравнением
. Ответ округлить с точностью до десятых.Решение.
Уравнение гиперболы в общем виде6
Найдем эксцентриситет гиперболы по формуле:
