ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 20
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Қазақстан Республикасы білім және ғылым министрлігі
«Ғұмарбек Дәукеев атындағы Алматы энергетика және байланыс
университеті» коммерциялық емес АҚ
Ақпараттық технологиялар институты
IT-инжиниринг кафедрасы
№2 ЗЕРТХАНАЛЫҚ ЖҰМЫС
бойынша
ЕСЕП БЕРУ
Пәннің атауы: Интеллектуалды ақпараттық жүйелерді құру негіздері
Тақырыбы: Matlab-та матрицалармен жұмыс
Тобы: ЭСХк 20-1
Орындаған: Алшора Әлия
Қабылдаған: аға оқытушы Кальпебаев А.
Алматы, 2022
Зертханалық жұмыс №2. Matlab-та матрицалармен жұмыс
Жұмыс мақсаты: MATLAB жүйесінің қолданушы интерфейсін және тура есептеу режиміндегі жүйенің жұмыс негізін зерттеу матрицалармен жұмыс жасап үйрену
Матрицалар
MatLab-та скаляр шама, вектор және матрицалармен есептеулер жүргізуге болады. MatLab - та кіші және бас әріптер айырылып жазылады, сондықтан p және P әр түрлі айнымалылар екендігін байқауымызға болады. Массивтердің енгізілуі үшін (векторлардың немесе матрицалардың) олардың элементтері квадрат жақшаларға алынып жазылады. Вектордың жол енгізуіне 1х3 өлшеммен келесі команда орындалады, онда жол элементтері пробелмен немесе үтірлермен бөлінеді.
Тапсырма
Магиялық матрица – magіc құрыңыз. Матрицаның ранг және базистік минорларын құрыңыз. Сызықты теңдеулер жүйесін шешіңіз.
Matlab-тың кез келген көлемді сиқырлы квадрат құрайтын функциясы бар (сиқырлы квадратта жол элементінің қосындысы баған элементтерінің қосындысына тең және ол басты және қосымша диагоналдар элементтерінің қосындысына тең). Сондықтан, бұл функция magіc деп аталады.
>>B=magic(4)
B=
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
Сызықты теңдеулер жүйесін шешу үшін кері матрица әдісін қолдануға болады, ол үшін келесі шарттарды орындау керек:
Берілген жүйедегі матрицаның коэффициенттерін ж/е вектор элементтерін келтіру;
Кері матрица әдісін қолдана отырып, белгісіз векторды матрицаның туындысы ретінде қарастыру арқылы жүйені шешу.
Мысалы,
Matlab-та шешімі:
A=[1 -2 1;2 -5 -1;-7 0 1];
b=[2;-1;-2];
x=inv(A)*b
Кері және жалған кері матрица алыңыз. Транспонирленген және комплексті түйіндес матрицалар құрыңыз.
Кері ж/е жалған кері матрица есептерін Matlab-та шешуге болады. Кері матирица есептерін шешу үшін inv функциясы қолданылады.
Мысалы,
Matlab-та шешімі:
A=[1 -2 1;2 -5 -1;-7 0 1]; b=[2;-1;-2]; x=inv(A)*b
Ал жалған кері матирица есептерін шешу үшін inv функциясы колд.
Траспорнирленген матрица векторлар секілді .’ көмегімен жазылады, ал ‘ символы комплексті түйінің білдіреді. Кейбір матрицаларда осы екі екеуі қолданғанда бірдей мән шығады.
>>B’
Ans=
4 2 5
7 1
1 0 2
>>B.’
Ans=
2 5
3 7 1
-
2
1. Тапсырмада магиялық матрица magic құру (1-сурет )
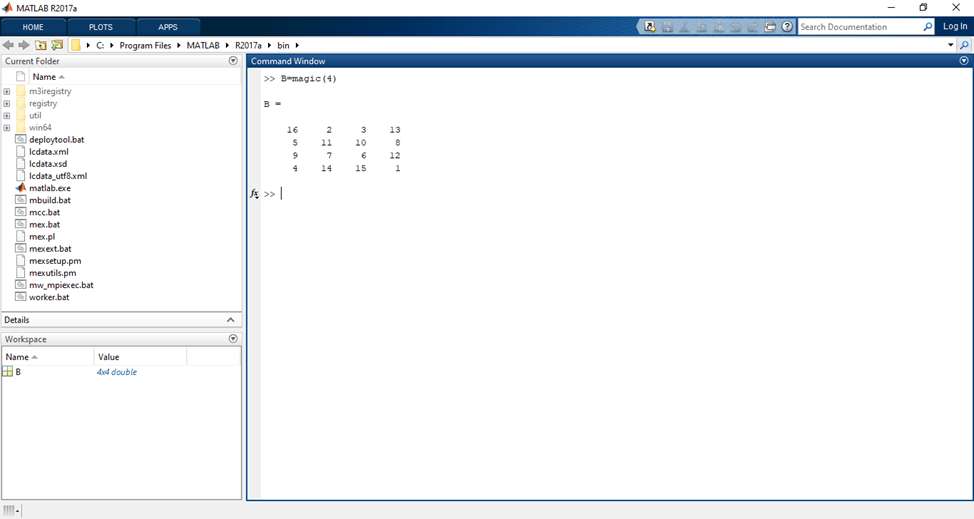
1-сурет – magic құру
2. Тапсырмада кері матрица есептерін inv арқылы есептеу ( 2-сурет )
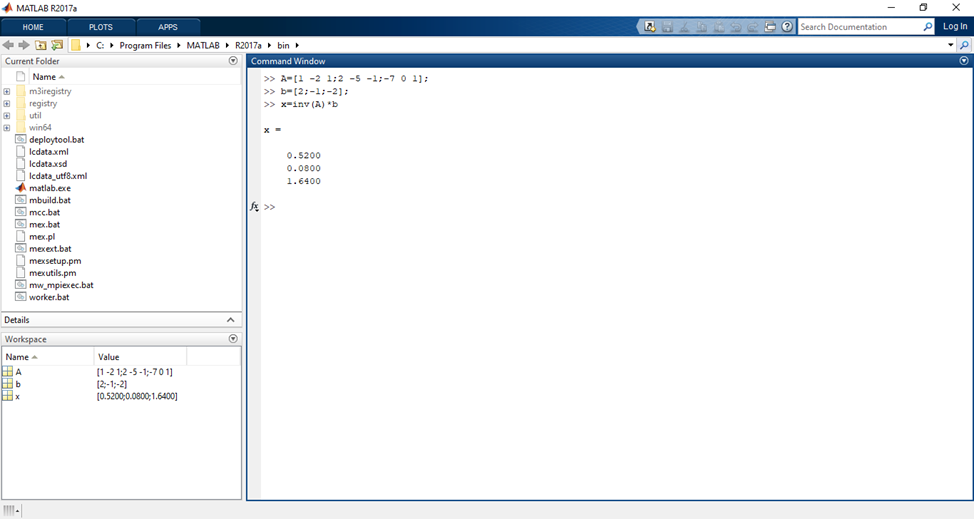
2- сурет – inv арқылы есептеу
Қорытынды
Мен бұл зертханалық жұмыста MATLAB-та матрицалармен жұмыс жасау болды. MATLAB жүйесінің қолданушы интерфейсін және тура есептеу режиміндегі жүйенің жұмыс негізін зерттеу матрицалармен жұмыс жасап үйрену болатын. Яғни 2 тапсырма берілген. Олар магиялық матрица құру және кері матрицаны есептеу.