Глоссарий. Теория множеств
Георг Кантор	Немецкий математик, ученик Вейерштрасса. Наиболее известен как создатель теории множеств.
Множество	Представляет собой набор, совокупность каких-либо объектов - элементов этого множества.
Элемент множества	Любой объект, входящий в состав множества.
Числовые множества	Это наборы чисел, объединенных в группы согласно какими-то общим свойствам
N – множество	Множество натуральных чисел.
Z – множество	Множество целых чисел.
Q – множество	Множество рациональных чисел.
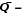множество	Множество иррациональных чисел.
R – множество	Множество действительных чисел.
C – множество	Множество комплексных чисел.
Множество считают заданным, если	Если о каждом элементе можно однозначно сказать, принадлежит он этому множеству или нет.
Способы задания множеств	1. это простое перечисление элементов множества 2. задать множество с помощью так называемого характеристического условия
Характеристическое свойство множеств	Это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
Конечное множество	Множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества.
Бесконечное множество	Множество, не являющееся конечным.
Пустое множество	Множество, не содержащее ни одного элемента
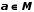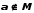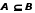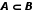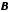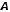Множество является подмножеством множества	если каждый элемент множества В является также элементом множества А. В этом случае множество А является надмножеством В.
Собственное подмножество Несобственное подмножество	Любое множество В среди своих множеств содержащие само себя и пустое множество. Само множество В и пустое множество называют несобственными подмножествами, остальные подмножества называют собственными.
Универсальное множество	Множество, содержащее все объекты и все множества
Парадокс Рассела	Парадокс можно описать следующим образом. Условимся называть множество «обычным», если оно не является своим собственным элементом. Например, множество всех людей является «обычным», так как само множество — не человек. Примером «необычного» множества является множество всех множеств так как оно само является множеством, а следовательно, само является собственным элементом
Отношения множеств	Отношение из двух элементов множества называют бинарным. Бинарные отношения множеств представляют собой некоторое множество упорядоченных пар, образованных декартовым произведением
Алгоритм определения вида отношения между двумя множествами А и В
Операции над множествами	Две самые важные операции, которые выполняют над множествами – это пересечение и объединение. Пересечение множеств часто записывают с помощью такой нотации: Пересечение определяет, где два множества пересекаются. Другими словами, эта операция возвращает все элементы, которые входят в два множества.
Бинарные операции	Бинарная, или другими словами двуместная операция, принимающая два аргумента и возвращающая один результат (то есть с арностью два )
Унарные операции	Это операция над одним операндом (побитовое отрицание, унарный минус – меняет знак числа)
Диаграммы Эйлера-Венна	Геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Первое их использование приписывают Леонарду Эйлеру. Используются в математике, логике, менеджменте и других прикладных направлениях.
Пересечением множеств А и В	Пересечением множеств А и В является множество их общих элементов, т.е. всех элементов, принадлежащих и множеству А, и множеству В. Пересечение множеств обозначается :
Объединением множеств А и В	Объединением множеств А и В является множество содержащее те и только те элементы, которые принадлежат множеству либо А либо В
Разностью множеств А и В	Разностью множеств А и В называется множество содержащее только те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В.
Дополнение к множеству А	Дополнением множества В до множества А называется множества, содержащее все элементы множества А, которые не принадлежат множеству В.
Симметрическая разность двух множеств	Одна из операций над множествами
Декартовым произведением множеств А и В	Множество, элементами которого являются все возможные упорядоченные пары элементов исходных множеств.
Приоритет выполнения операций	Приоритет операций – очерёдность выполнения операции в выражении, при условии что в выражении нет явного указания порядка следования выполнения операций (с помощью круглых скобок). Если операции имеют одинаковый приоритет. То очерёдность выполнения таких операций определяется согласно свойству ассоциативности.
Разбиение множества на классы	Так как разбитие множества на классы связано с выделением его подмножеств, то классификацию можно выполнять при помощи свойств элементов множеств.
Классификация	Это действие распределения объектов по классам на основании сходств внутри класса и их отличия от других объектов.
Дихотомическая классификация	Это задача классификации элементов заданного множества в две группы (предсказание, какой из групп принадлежит каждый элемент множества) на основе правила классификации.
Формула включения-исключения
Закон Моргана. Для множеств А и В: 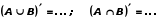.	Логические правила, связывающие пары логических операций при помощи логического отрицания. Названы в честь шотландского математика Огастеса де Моргана. В краткой форме звучат так: Отрицание конъюнкции есть дизъюнкция отрицаний. Отрицание дизъюнкции есть конъюнкция отрицаний.
Переместительный закон (коммутативность) для операций объединения и пересечения	свойство алгебраической операции, выражающее независимость суммы или произведения от перестановки слагаемых или сомножителей, напр. а + b = b + а; ab = ba.
Сочетательный закон (ассоциативность) для операций объединения и пересечения	Свойство операций сложения и умножения чисел, выражаемое тождествами (а + b) + c = a + (b + c) и (ab)c = a(bc). В общем смысле, действие а * b называется ассоциативным, если (а * b) * c = а * (b * с)
Распределительный закон (дистрибутивность) пересечения относительно объединения множеств	Свойство согласованности ассоциативной и коммутативной операций, определённых на одном и том же множестве
Распределительный закон объединения относительно пересечения множеств	Если операции объединения множеств поставить в соответствие операцию сложения чисел, операции пересечения – операцию умножения, универсальному множеству – единицу, а пустому множеству – ноль, то возникает аналогия между множествами и числами.
Законы поглощения
Универсальное и пустое множества являются	Множество всех вещественных чисел. Пустое множество обозначается знаком, оно не содержит ни одного элемента. Иногда полезно считать, что существует некое универсальное множество, содержащие все элементы.

---

---

Смотрите также файлы

• Религиознотрадиционные правовые системы.docx

• Надлежащая аптечная практика(gpp). Основные принципы gpp.docx

• Ткани человека.docx

• Эсн и эо электромеханического цеха.docx

• Организация бухгалтерского учета.docx