I. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Рабочая программа составлена на основе федерального государственного стандарта основного общего образования по математике 2004 г, Примерной программы по математике основного общего образования (Просвещение 2016г), УМК Атанасяна Л.С., и др. «Геометрия, 10-11» (Просвещение, 2016г.), основной образовательной программы школы на 2021-2022 учебный год.

Рабочая программа ориентирована на использование дополнительных пособий для учащихся:

• 
  Энциклопедия. Я познаю мир. Математика.-М.: ООО «Издательство АСТ»,2016;
  
• 
  За страницами учебника геометрии.
  

и для учителя:

• 
  Изучение геометрии в 10-11 классах: методические рекомендации : кн. для учителя / С.М. Саакян, В.Ф Бутузов и др. – М.: Просвещение,
  
• 
  А.И Медняк Контрольные и проверочные работы по геометрии 7-11 классы: Москва «Дрофа»,г
  
• 
  Геометрия 10-11Дидактический материал по стереомеории./ Г.И. Ковалёва – Волгоград, «Учитель»,
  
• 
  Сугоняев И.М. Геометрия 10 класс. Тесты в 2-х частях –
  
• 
  В.А. Яровенко Поурочные разработки по геометрии к учебному комплекту Л.С. Атанасяна и др.
  

В рабочей программе представлены содержание математического образования, требования к обязательному и возможному уровню подготовки обучающегося и выпускника, виды контроля, а также компьютерное обеспечение урока.
  Цели обучения.
      Школьное математическое образование ставит следующие цели обучения:

• 
  овладение конкретными математическими знаниями, необходимыми для применения в практической     деятельности, для изучения смежных дисциплин, для продолжения образования;
  
• 
  интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для повседневной жизни;
  
• 
  формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
  
• 
  формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
  

Задачи курса геометрии для достижения поставленных целей:
-систематическое изучение свойств геометрических тел в пространстве;

-формирование умений применять полученные знания для решения практических задач;

-формирование умения логически обосновывать выводы для изучения школьных естественнонаучных дисциплин на базовом уровне.

---

Общая характеристика учебного предмета.
Геометрия- один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Место предмета в базисном учебном плане.
Согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации для обязательного изучения геометрии на этапе среднего (полного) общего образования отводится 70 часов ( 2 часа в неделю). Учебная нагрузка 35 недель.
Предусмотрены 4 контрольные тематические работы, зачёты, практические работы.
  При планировании учебного времени на освоение курса геометрии 10 класса, предусмотрены:

• 
  использование электронных учебных пособий,
  
• 
  применение современных информационных технологий компьютерных и мультимедийных продуктов;
  
• 
  интерактивное оборудование.
  

Оставляю за собой право в течении учебного года добавлять количество часов на изучение отдельных тем за счёт повторения в конце учебного года, если на то будут причины (плохое усвоение темы), а также вносить изменения в тексты к/р по той же причине .

II. Содержание учебного предмета.
Тема 1. «Введение. Аксиомы стереометрии и их следствия» (5 часов)

 

Раздел математики. Сквозная линия

• 
  Геометрические тела и их свойства.
  
• 
  Измерение геометрических величин.
  

Обязательный минимум содержания образовательной области математика

• 
  Предмет стереометрии.
  
• 
  Аксиомы стереометрии. Некоторые следствия из аксиом.
  

Требования к математической подготовке

Иметь представление о содержании предмета стереометрии. Знать аксиомы стереометрии и их следствия.

Уровень обязательной подготовки обучающегося

• 
   Иметь представление о содержании предмета стереометрии.
  
• 
  Знать аксиомы стереометрии и их следствия.
  

Уровень возможной подготовки обучающегося

• 
   Иметь представление о содержании предмета стереометрии , об аксиоматическом методе построения геометрии.
  
• 
  Знать аксиомы стереометрии и их следствия, уметь применять их при решении задач.
  

---

Уровень обязательной подготовки выпускника

• 
  Верно ли утверждение: если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?
  

 

Уровень возможной подготовки выпускника

• 
  Три прямые проходят через одну точку. Через каждые две из них проведена плоскость. Сколько всего проведено плоскостей?
  

Тема 2. «Параллельность прямых и плоскостей» (19 часов)
Раздел математики. Сквозная линия

• 
  Геометрические тела и их свойства.
  
• 
  Измерение геометрических величин.
  

Обязательный минимум содержания образовательной области математика

• 
  Взаимное расположение прямых и плоскостей в пространстве.
  
• 
  Угол между двумя прямыми.
  
• 
  Параллельность прямых и плоскостей.
  
• 
  Признаки параллельности прямых и плоскостей.
  

Требования к математической подготовке
Уровень обязательной подготовки обучающегося

• 
  Знать определения параллельных прямых и плоскостей, их взаимное расположение в пространстве.
  
• 
  Знать признаки параллельности прямых и плоскостей.
  
• 
  Уметь решать простые задачи по этой теме.
  

Уровень возможной подготовки обучающегося

• 
  Знать определения параллельных прямых и плоскостей, их взаимное расположение в пространстве, признаки параллельности прямых и плоскостей.
  
• 
  Уметь решать задачи по этой теме, правильно выполнять чертеж по условию стереометрической задачи, понимать стереометрические чертежи.
  
• 
  Уметь решать задачи на доказательство, строить сечения геометрических тел.
  

Уровень обязательной подготовки выпускника

• 
  Параллельные плоскости α и β пересекают сторону АВ угла ВАС соответственно в точках А₁ и А₂, а сторону АС этого угла – соответственно в точках В₁ и В₂. Найдите АА₂ и АВ₂, если А₁А₂ = 2А₁А, А₁А₂=12 см, АВ₁=5 см.
  

 

Уровень возможной подготовки выпускника

• 
  Стороны АВ и ВС параллелограмма АВСD пересекают плоскость α . Докажите, что прямые AD и DC также пересекают плоскость α.
  
• 
  Проведите сечение прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ , проходящее через вершину А, В и середину ребра СС₁.
  

Тема 3. «Перпендикулярность прямых и плоскостей» (20 часов)

---

 

Раздел математики. Сквозная линия

• 
  Геометрические тела и их свойства.
  
• 
  Измерение геометрических величин.
  

Обязательный минимум содержания образовательной области математика

• 
  Перпендикулярность прямых в пространстве.
  
• 
  Углы между прямыми и плоскостями, между плоскостями.
  
• 
  Признак перпендикулярности прямой и плоскости.
  

Требования к математической подготовке

 

Уровень обязательной подготовки обучающегося

• 
  Знать определения перпендикулярных прямых и плоскостей.
  
• 
  Знать о перпендикуляре и наклонных в пространстве.
  
• 
  Понимать сущность углов между прямыми, между прямыми и плоскостями, между плоскостями в пространстве.
  
• 
  Знать признак перпендикулярности прямой и плоскости.
  
• 
  Уметь решать простые задачи по этой теме.
  

Уровень возможной подготовки обучающегося

• 
  Уметь анализировать взаимное расположение объектов в пространстве.
  
• 
  Решать стереометрические задачи на нахождение геометрических величин (длин, углов, площадей).
  

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• 
  исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
  

Уровень обязательной подготовки выпускника

• 
  Отрезок ВМ перпендикулярен к плоскости прямоугольника АВСD. Докажите, что прямая CD перпендикулярна к плоскости МВС.
  

 

Уровень возможной подготовки выпускника

• 
  Правильные треугольники АВС и МВС расположены так, что вершина М проецируется в центр треугольника АВС. Вычислите угол между плоскостями этих треугольников.
  
• 
  Проведите сечение прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ , проходящее через вершину А, В и середину ребра СС₁.
  

 

Тема 4. «Многогранники» (12 часов)

 

Раздел математики. Сквозная линия

• 
  Геометрические тела и их свойства.
  
• 
  Измерение геометрических величин.
  

Обязательный минимум содержания образовательной области математика

• 
  Понятие многогранника.
  
• 
  Призма.
  
• 
  Пирамида. Усеченная пирамида.
  
• 
  Правильные многогранники.
  

Требования к математической подготовке
 Уровень обязательной подготовки обучающегося

• 
  Понимать, что такое многогранник.
  
• 
  Уметь определять вид многогранника.
  
• 
  Знать свойства многогранников.
  
• 
  Уметь решать несложные задачи на свойства многогранников, на определение площади их поверхности, на построение сечений многогранников плоскостью.
  

---

Уровень возможной подготовки обучающегося

• 
  Уметь правильно выполнять чертеж по условию стереометрической задачи.
  
• 
  Понимать стереометрические чертежи.
  
• 
  Уметь решать задачи на доказательство.
  

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• 
  исследования (моделирования) практических ситуаций на основе изученных формул и свойств фигур;
  
• 
  вычисления площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
  

Уровень обязательной подготовки выпускника

• 
  Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 см. Найдите площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.
  
• 
  Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналей равна 8 см. Найдите боковые ребра пирамиды, если высота ее проходит через точку пересечения диагоналей основания и равна 7 см.
  

 Уровень возможной подготовки выпускника

• 
  В основании пирамиды SABC лежит равнобедренный треугольник АВС с основанием ВА, равным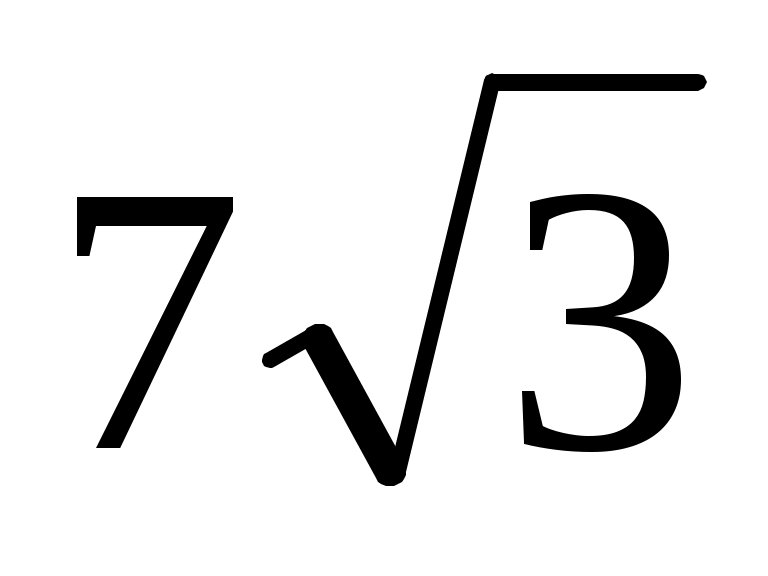 см. Ребро SС перпендикулярно плоскости основания пирамиды. Грань SAB наклонена к плоскости основания под углом в 60⁰. Найдите площадь боковой поверхности пирамиды.
  
• 
  Постройте сечение четырехугольной пирамиды PABCD плоскостью, проходящей через точки L,N и M, принадлежащим соответственно ребрам РА, РD и ВС.
  

Тема 5. «Векторы в пространстве» (7 часов)

 

Раздел математики. Сквозная линия

• 
  Геометрические тела и их свойства.
  
• 
  Измерение геометрических величин.
  

Обязательный минимум содержания образовательной области математика

• 
  Понятие вектора в пространстве.
  
• 
  Сложение и вычитание векторов.
  
• 
  Умножение вектора на число.
  
• 
  Компланарные векторы.
  

Требования к математической подготовке
 Уровень обязательной подготовки обучающегося

• 
  Знать определение вектора, свойства векторов.
  
• 
  Уметь производить действия с векторами.
  
• 
  Уметь решать несложные задачи с применением векторного метода.
  

Уровень возможной подготовки обучающегося

• 
  Уметь правильно выполнять чертеж по условию задачи.
  
• 
  Овладеть векторным методом решения задач различной сложности.
  
• 
  Уметь решать задачи на доказательство.
  

---

Смотрите также файлы

• Устройство, разведка и преодоление инженерных заграждений, элементы новых технологий.docx

• Практическая работа 4.rtf

• Программа xix международной Бурденковской научной конференции, посвященной Десятилетию науки и технологий.docx

• Древний Египет одна из самых загадочных и интересных цивилизаций, которая возникла на территории Африки более 5000 лет назад.docx

• Сценарий к спортивному празднику 23 февраля. В старшей группе и подготовительной группе.docx